Разработка программ для вычисления площади криволинейной фигуры для Turbo Pascal

1 Метод прямоугольников
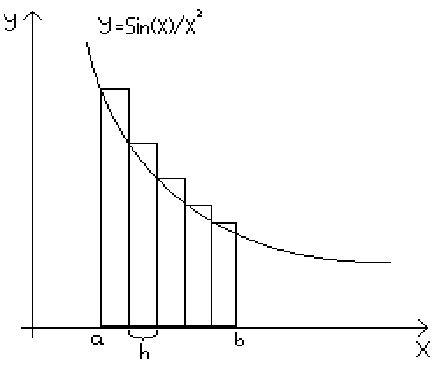
1.1 Суть этого метода заключается в том, что мы разрежем фигуру на множество тонких прямоугольных полосок и, умножая длину на ширину полосок и складывая всѐ в общую сумму, получим значение искомой площади. Шаг выбираем самостоятельно: h=(b-a)/100. Соответственно, чем меньше шаг, тем больше точность.

Различают:

1. Метод правых прямоугольников;
2. Метод левых прямоугольников;
3. Метод средних прямоугольников.

1.2.1 Пример 1

Программа для метода правых прямоугольников:

Program Olly;
var a,b,h,S1,x,y:real;
begin
S1:=0;
readln(a);
readln(b);
h:=(b-a)/100;
x:=a;
while x do begin
y:=sin(x)/sqr(x);
S1:=S1+(y)*h;
x:=x+h;
end;
writeln(S1);
end.

Программа метода левых прямоугольников:

Program Olly;
var a,b,h,S1,x,y,u:real;
begin
S1:=0;
readln(a);
readln(b);
h:=(b-a)/100;
x:=a+h;
u:=b-h
while x<=u
do begin
y:= sin(x)/sqr(x);
S1:=S1+(y)*h;
x:=x+h;
end;
writeln(S1);
end.

Программа для метода средних прямоугольников:
Program Olly;
var a,b,h,S1,S2,S3,x,y,R:real;
begin
S1:=0;
S2:=0;
readln(a);
readln(b);
h:=(b-a)/100;
x:=a;
while x do begin y:=sin(x)/sqr(x);
S1:=S1+(y)*h;
x:=x+h;
end;
x:=a;
while x do begin
y:=sin(x)/sqr(x);
S2:=S2+(y)*h;
x:=x+h;
end;
R:=S1-S2;
R:=R/2;
S3:=S1-R;
writeln(S3);
end.

1.2.2 Пример 2 

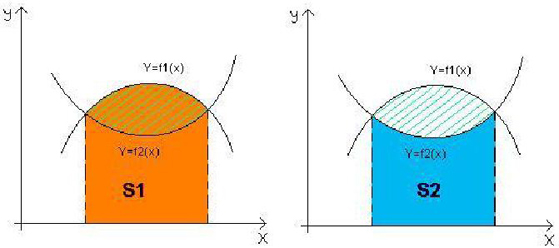
Площадь образованной фигуры вычисляется как разность площади криволинейной фигуры, ограниченной графиком функции y1=f1(x), осью OX и перпендикулярами к оси OX, проходящими через точку A и B, и площади криволинейной фигуры, ограниченной графиком функции y2=f2(x), осью OX и перпендикулярами к оси OX, проходящими через точки A и B. А значит для вычисления площади, нам понадобиться формула: S3=S1-S2. 

Программа для нахождения площади методом прямоугольников:
Program Olly;
var a,b,h,S1,S2,S3,x,y2,y1:real;
begin
S1:=0;
S2:=0;
readln(a);
readln(b);
h:=(b-a)/100;
x:=a;
while x do begin
y1:=f1(x);
S1:=S1+(y1)*h;
y2:=f2(x);
S2:=S2+(y2)*h;
x:=x+h;
end;
S3:=abs(S1-S2);
writeln(S3);
end.

2 Метод трапеции
2.1. Для этого метода разрежем фигуру на множество тонких полосок, эти полоски образуют криволинейные трапеции. Площадь образованной фигуры вычисляется как сумма площадей криволинейных трапеций. Площади трапеции определяется по формуле S=H(L+R)/2. Выведем формулу для вычисления площади методом трапеции:

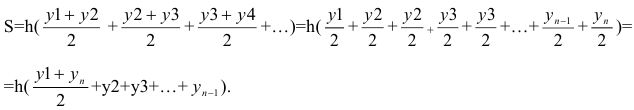
2.2 Программа для метода трапеции:
Program Olly;
var a,b,h,Su,S,x,y:real;
begin
Su:=0;
readln(a);
readln(b);
h:=(b-a)/100;
x:=a;
while x do begin
y:=f(x);
if (x=a)or(x=b)
then y:=y/2;
Su:=Su+y;
x:=x+h;
end;
S:=Su*h;
writeln(S);
end.

3 Метод парабол

3.1 Этот метод даѐт результат высокой точности для параболы и фигур, близких по кривизне к параболе. Идея метода исходит из того, что на частичном промежутке дуга некоторой параболы в общем случае теснее прилегает к кривой y=f(x), чем хорда, соединяющая концы дуги этой кривой, и поэтому значения площадей соответствующих элементарных трапеций, ограниченных “сверху” дугами парабол, являются более близкими к значениям площадей соответствующих частичных криволинейных трапеций, ограниченных сверху дугой кривой y=f(x), чем значения площадей соответствующих прямолинейных трапеций. Сущность метода заключается в следующем. Отрезок [a, b] делится на 2n равных частей. Пусть точки деления будут х0=а, x1, x2, …x2n-2, x2n-1, x2n=b, а y0, y1, …y2n – соответствующие значения функции на отрезке [a,b]. Произведем квадратичную интерполяцию данной функции на каждом из отрезков разбиения, т.е. заменим дугу графика дугой параболы с вертикальной осью.

Для нахождения площади криволинейной фигуры нужно использовать формулу: S=h/3*(y1+4y2+2y3+4y4+2y5+…+4y4+2yn-2+yn).

3.2. Программа для метода парабол:
Program Olly;
var m,y,x,Su,S:real; a,b,h:integer;
begin
Su:=0;
readln(a);
readln(b);
h:=b-a;
m:=h/100;
x:=a;
while x do begin
y:=f(x);
if (x=a)or(x=b)
then y:=y
else
if round(y) mod 2=0
then y:=4*y
else y:=2*y;
Su:=Su+y;
x:=x+m;
end;
S:=Su*(m/3);
writeln(S);
end.

4 Другие методы

4.1 «Каверзные» случаи
К «каверзным» случаям относятся фигуры с бесконечно большой площадью.

С задачей справится метод прямоугольников. Так как мельчайшие доли не имеют значения, поэтому в этом случае ограничиваем бесконечную площадь.

4.2 Метод Монте-Карло
К экстравагантным методам вычисления площади криволинейной фигуры является способы, основанные на использовании случайных чисел (объединѐнные под общим названием Монте-Карло). При использовании данного метода суммирования производиться в точках, выбранных случайным образом. Как это ни парадоксально, но совершенно случайно помогает в вычислении строго определѐнного. Более того, часто такой путь решения лучше, чем какие-либо формульные ухищрения.