Цель урока:
Дидактическая: закрепить изученный материал: правила нахождения первообразных; выработать у студентов навыки использования теории по нахождению площади криволинейной трапеции;
научить вычислять площадь фигуры, ограниченной линиями; работа на компьютере.
Развивающая: развивать творческую сторону логического мышления, исследовательские навыки, навыки использования интерактивного оборудования.
Воспитательная: воспитывать умение работать в группе: «чувство локтя» и индивидуальную ответственность за достижение результата.
План урока:
1. Организационный момент- (5 мин)
2. Опрос пройденного материала - ( 15 мин)
3. Изучение нового материала – (35 мин )
4. Закрепление изученного материала – (25 мин)
5. Итог урока – (5мин).
6. Домашнее задание – (5 мин)
Ход урока
1. Организационный момент: целевая установка, отметка отсутствующих, психологический настрой.
Группу разбиваю на 4 подгруппы, раздаю листочки для самооценки.
2. Опрос пройденного материала:
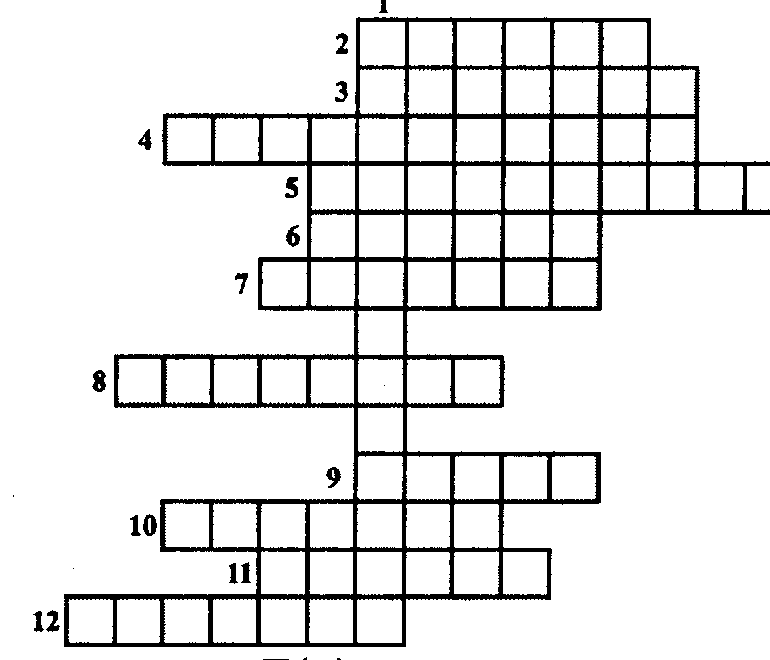
Отгадывание кроссворда. Студенты должны показать свои теоретические знания на минимальном уровне. Кроссворд пишется на отдельных листах и выдается каждой команде. За каждое правильно угаданное слово команда получает 1 балл. Это задание на скорость, и команда, которая первой отгадала кроссворд, получает дополнительно 4 балла.
Максимальное количество баллов, которое может получить команда, равно 10. Время выполнения задания 5 минут.
Вопросы кроссворда:
1. Как называется функция F(x)?
2. Что является графиком функции y = ax + b ?
3. Самая низкая школьная отметка?
4. Какой урок обычно проходит перед зачетом?
5. Синоним слова «дюжина»
6. Есть в каждом слове, у растения и, может быть, у уравнения.
7. Что можно вычислить при помощи интеграла?
8. Одно из важнейших понятий математики.
9. Форма урока, на котором проводится проверка знаний.
10. Немецкий ученый, в честь которого названа формула, связывающая площадь криволинейной трапеции и интеграла.
Сегодня на занятии мы получим возможность через обсуждение вопросов теории по теме «Интеграл» применять их в процессе нахождения площади криволинейной трапеции, используя навыки исследовательской деятельности. Я раздаю в каждую команду листочки с написанными терминами. Ваша задача построить ассоциативную цепочку.
Математика - математический анализ – предел – дифференцирование.
Математика - математический анализ – производная по времени – скорость тела Математика - дифференцирование – геометрический смысл- касательная к графику.
Математика - дифференцирование – интегрирование - криволинейная трапеция.

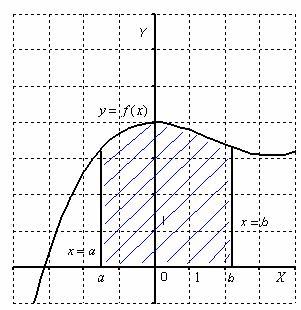
4. Закрепление изученного материала: Найти площадь криволинейной трапеции, ограниченной линиями у= cos x, e=0, x= -π/3, x=π/6
Работа с электронными учебниками. Задания.
5. Итог урока
6. Домашнее задание:
Алимов ША, стр 305 № 1022
Весь материал – смотрите документ.

 Получите свидетельство
Получите свидетельство Вход
Вход



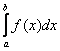 .
. 








 Конспект урока по математике "Вычисление площадей фигур с помощью определенного интеграла" (0.14 MB)
Конспект урока по математике "Вычисление площадей фигур с помощью определенного интеграла" (0.14 MB)
 0
0 1301
1301 122
122 Нравится
0
Нравится
0


