Перевод чисел в позиционных системах счисления
Перевод чисел в десятичную систему счисления
Перевод числа из двоичной системы в десятичную. Возьмем любое двоичное число, например 10,11 2 . Запишем его в развернутой форме и произведем вычисления:
10,11 2 = 1* 2 1 + 0 * 2 -1 + 1 * 2 -2 = 1 * 2 + 0 * 1 + 1 * 1 / 2 + 1 * 1 / 4 = 2,75 10
Перевод чисел из восьмеричной системы в десятичную . Возьмем любое восьмеричное число, например 67,5 8 Запишем его в развернутой форме и произведем вычисления:
67,5 8 = 6 * 8 1 + 7 * 8 0 + 5 * 8 -1 = 6 * 8 + 7 * 1 + 5 * 1 / 8 + 55,625 10
Перевод чисел из шестнадцатеричной системы в десятичную.
Возьмем любое шестнадцатеричное число, например 19F 16 Запишем его в развернутой форме (при этом необходимо помнить, что шестнадцатеричная цифра F соответствует десятичному числу 15) и произведем вычисления:
19F 16 = 1 * 16 2 + F * 16 0 = 1 * 256 + 9 * 16 + 15 * 1 = 415 10
Задание
- перевести в десятичную систему следующие числа:
101 2 , 110 2 , 111 2 , 7 8 , 11 8 , 22 8 , 1А 16 , ВF 16 , 9С 16 .
Перевод чисел из десятичной системы в двоичную, восьмеричную и шестнадцатеричную.
Алгоритм перевода целых десятичных чисел в двоичную систему счисления.
Пусть А цд - целое десятичное число. Запишем его в виде суммы степеней основания 2 с двоичными коэффициентами. В его записи в развернутой форме будут отсутствовать отрицательные степени основания (числа 2):
А цд = а n-1 * 2 n -1 + а n – 2 + …. + а 1 * 2 1 + а 0 * 2 0
На первом шаге разделим число А цд на основание двоичной системы, то есть на 2. частное от деления будет равно
a n - 1 * 2 n-2 + a n-2 * 2 n-3 + …. + a 1 ,
а остаток – равен a 0.
На втором шаге целое частное опять делим на 2, остаток от деления будет теперь равен a 1 .
Если продолжить этот процесс деления, то после n-го шага получим последовательность остатков:
а 0 , а 1 , …., а n-1 .
Алгоритм перевода целого десятичного числа в двоичное будет следующим:
- Последовательно выполнять деление исходного целого десятичного числа и получаемых целых частных на основание системы (на 2) до тех пор, пока не получится частное, меньшее делителя, то есть меньшее 2.
- Записать полученные остатки в обратной последовательности.
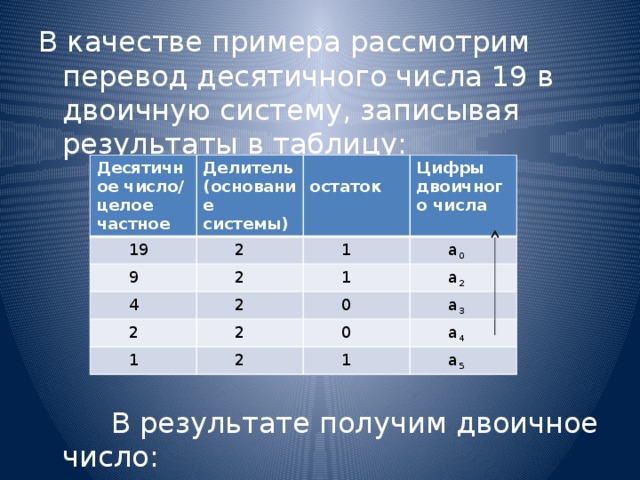
В качестве примера рассмотрим перевод десятичного числа 19 в двоичную систему, записывая результаты в таблицу:
В результате получим двоичное число:
А 2 = а 4 а 3 а 2 а 2 а 1 а 0 = 10011 2 .
Десятичное число/ целое частное
19
Делитель
(основание системы)
2
9
4
2
1
Цифры двоичного числа
остаток
2
а 0
1
2
а 2
0
2
1
а 3
2
0
а 4
1
а 5
Алгоритм перевода правильных десятичных дробей в двоичную систему счисления.
Пусть А дд – правильная десятичная дроби. В ее записи в развернутой форме будут отсутствовать положительные степени основания (числа 2).
А дд = а -1 * 2 -1 + а -2 * 2 -2 + …
На первом шаге умножим число А дд на основание двоичной системы, то есть на 2. произведение будет равно:
А дд = а -1 + а -2 * 2 -1 + …
Целая часть будет равна а -1 .
На втором шаге оставшуюся дробную часть опять умножим на 2, получим целую часть, равную а -2.
описанный процесс необходимо продолжать до тех пор, пока в результате умножения мы не получим нулевую дробную часть или не будет достигнута требуемая точность выражений.
Алгоритм перевода правильной десятичной дроби в двоичную будет следующим:
1. Последовательно выполнять умножение исходной десятичной дроби и получаемых дробных частей произведений на основание системы до тех пор, пока не получится нулевая дробная часть или не будет достигнута требуемая точность вычислений.
2. Записать полученные целые части произведения в прямой последовательности.
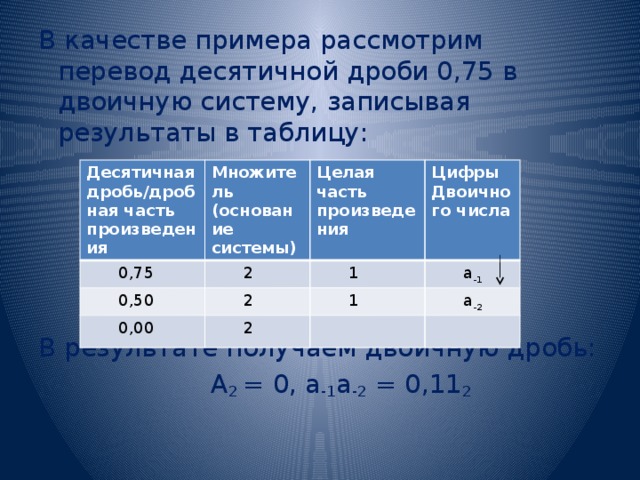
В качестве примера рассмотрим перевод десятичной дроби 0,75 в двоичную систему, записывая результаты в таблицу:
В результате получаем двоичную дробь:
А 2 = 0, а -1 а -2 = 0,11 2
Десятичная дробь/дробная часть произведения
Множитель
0,75
2
(основание системы)
0,50
Целая часть произведения
1
2
0,00
Цифры
а -1
Двоичного числа
2
1
а -2
Перевод чисел из системы с основанием р в систему с основанием q
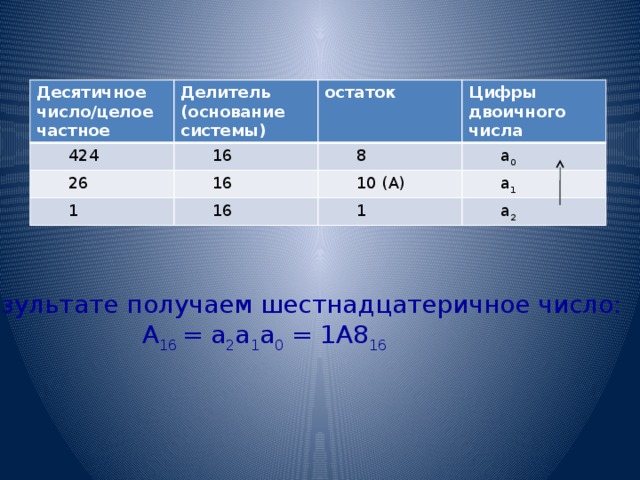
Рассмотрим алгоритм перевода целых чисел на примере перевода целого десятичного числа А 10 = 424 10 в шестнадцатеричную систему, то есть из системы счисления с основанием р=10 в систему счисления с основанием q= 16.
В процессе выполнения алгоритма необходимо обратить внимание, что все действия необходимо осуществлять в исходной системе счисления (в данном случае десятичной), а полученные остатки записывать цифрами новой системы счисления (в данном случае шестнадцатеричной).
Десятичное число/целое частное
424
Делитель
26
(основание системы)
остаток
16
1
16
8
Цифры двоичного числа
а 0
10 (А)
16
а 1
1
а 2
В результате получаем шестнадцатеричное число:
А 16 = а 2 а 1 а 0 = 1А8 16
задания
- Перевести целые десятичные числа
9 10 , 17 10 и 243 10 в двоичную, восьмеричную и шестнадцатеричную системы счисления.
- Перевести десятичные дроби 0,2 10 и 0,35 10 в двоичную, восьмеричную и шестнадцатеричную системы счисления с точностью до трех знаков после запятой.
- Перевести десятичные числа 3,5 10 и 47,85 10 в двоичную, восьмеричную и шестнадцатеричную системы счисления с точностью до трех знаков после запятой.
Получите свидетельство
Вход
Перевод чисел в позиционных системах счисления (89.72 КB)
0
1144
2
Нравится
0
