Цель урока:
Обобщить и закрепить знания об основных понятиях позиционных систем счисления на примере двоичной системы счисления.
Задачи урока:
активизировать познавательную деятельность учащихся;
помочь в развитии логического мышления;
показать применение игровых ситуаций на уроке.
План урока:
1.Организационный момент.
2.Повторение и обобщение предыдущих знаний.
3.Мотивация рассмотрения двоичной системы счисления.
4.Физкультминутка. Демонстрация решения задачи, связанной с переводом десятичного числа в двоичную систему счисления пальцевым методом.
5.Решение упражнений.
6.Домашнее задание.
7.Подведение итогов урока (рефлексия).
Оборудование и программное обеспечение:
Мультимедийный комплекс, презентация, созданная в программе MS PowerPoint.
ХОД УРОКА
1. Организационный момент.
Цель: Подготовить учащихся к работе на уроке
Задачи: быстрое включение учащихся в деловой ритм; организация внимания всех учащихся.
Взаимные приветствия учителя и учащихся; фиксация отсутствующих; проверка готовности учащихся к уроку; организация внимания и внутренней готовности; постановка цели урока.
2. Повторение и обобщение предыдущих знаний.
Цель: Повторение учащимися основных понятий позиционных и не позиционных систем счисления
Задачи: Установить осознанность всеми учащимися основных понятий пройденной темы; устранить в ходе проверки обнаруженные пробелы в знаниях; совершенствуя при этом знания, умения, навыки.
Повторение учащимися основных понятий позиционных систем счисления может быть организовано в виде игры по принципу «домино» (карточка делится пополам на вопрос-ответ, разрезаются и раздаются, дети ищут ответ на вопрос). Можно предложить следующие вопросы.
Вопрос № 1:
Система счисления – это способ записи чисел с помощью заданного набора специальных знаков (цифр).
Вопрос № 2:
Количество цифр, используемых в системе счисления для записи чисел, называется ее основанием.
Учитель: Существуют позиционные и не позиционные системы счисления.
Вопрос № 3:
Не позиционной системой счисления называется система, в которой вес цифры (т.е. тот вклад, который она вносит в значение числа) не зависит от ее позиции в записи числа.
Вопрос № 4:
Позиционной системой счисления называется система, в которой вес каждой цифры измеряется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число.
Учитель: Поскольку за основание системы счисления можно принять любое натуральное число, то существует бесчисленное множество позиционных систем счисления. Рассмотрим традиционные из них.
3. Мотивация рассмотрения двоичной системы счисления.
Цель: организовать целенаправленную работу учащихся, включить их в деловой ритм; обосновать важность изучения темы «Двоичная система счисления».
Задачи: показ практической значимости темы; постановка перед учащимися учебной проблемы.
Учитель: (читает стихотворение)
СКОЛЬКО ЛЕТ ДЕВОЧКЕ
(А. Стариков) – смотрите документ
Учитель: Ответить на эти вопросы вы сможете в конце нашего сегодняшнего урока.
Учитель: Люди предпочитают десятичную систему счисления вероятно потому, что с древних времен они считали по пальцам, а пальцев у людей по 10 на руках и ногах. Десятичная система счисления пришла к нам из Индии.
Но не всегда и везде используют десятичную систему счисления. В Китае, например, долгое время пользовались пятеричной системой счисления. Для общения с ЭВМ используют, кроме десятичной, двоичную, восьмеричную и шестнадцатеричную системы счисления. Из всех систем счисления особенно проста и поэтому интересна для технической реализации в ЭВМ двоичная система счисления.
Эта система имеет ряд преимуществ перед другими системами:
для ее реализации нужны технические элементы с двумя возможными состояниями (есть ток, нет тока; включено, выключено и т.д. Одному из состояний ставится в соответствие 1, другому – 0), а не десять, как в десятичной системе,
представление информации посредством только двух состояний надежно и помехоустойчиво,
упрощается выполнение арифметических действий,
возможность использовать аппарат булевой алгебры для выполнения логических преобразований информации.
Используя знания предыдущего урока заполним следующую таблицу «Сведения о двоичной системе» - смотрите документ
При заполнении таблицы учащиеся ориентируются на знания десятичной системы счисления и знания предыдущего урока. Каждый этап таблицы дополняется и разъясняется учителем, делаются выводы.
Попробуем составить таблицу первых 10 двоичных чисел.
Учитель: Сколько потребуется разрядов для записи цифры двоичного числа?
Ученики вычисляют: 23 = 8, 24 = 16. Значит для записи цифры двоичного числа достаточно 4 разрядов.
Учитель: составим таблицу первых десяти двоичных чисел – смотрите документ
При наличии времени (и более сильным учащимся) можно предложить продолжить данную таблицу, формируя натуральный ряд чисел двоичной системы счисления.
Вывод: недостаток двоичной системы – это быстрый рост числа разрядов, необходимых для записи чисел.
Учитель: оказывается, что мы с вами повторили открытие одного немецкого ученого математика Вильгельма Готфрида Лейбница (1646-1716).
Медаль, нарисованная В.Г Лейбницем, поясняет соотношение между двоичной и десятичной системами счисления.
Историческая справка – смотрите документ
4. Физкультминутка (демонстрация решения задачи, связанной с переводом десятичного числа в двоичную систему счисления пальцевым методом).
Цель: создать здоровьесберегающие моменты на уроке.
Задачи: научить применять упражнения для расслабления мышц рук.
Учитель: постарались вы на славу, предлагаю отдохнуть. Выполним зарядку для рук. Будем показывать числа, которые переведём в двоичную систему счисления.
Смысл перевода прост: нумеруем на одной руке (левой, ладонь к себе) от мизинца до большого пальца разряды от 0 до 4, что соответствует числам в десятичной системе 1,2,4,8,16. Считая, что 0- это согнутый палец, а 1 – оттопыренный, при решении задач, связанных с переводом целых чисел в двоичную из десятичной системы счисления требуется лишь сложить эти цифры, соответствующие загнутым пальцам. Данное упражнение, основанное на самом древнем способе- счете на пальцах, подразумевает развёрнутую форму записи числа в двоичной системе счисления. (Две руки можно использовать для перевода целых чисел до 512, так и для перевода дробных конечных чисел, где левая рука – целая часть числа, а правая – дробная). Учитель говорит число в десятичной системе (до 31 или 62), а школьники устно переводят число на пальцах в двоичную систему и записывают ответ. Для больших чисел приводится сам развёрнутый способ перевода числа из двоичной системы счисления в десятичную с примером.
Данное упражнение вносит эмоциональный характер, но требует внимания от учащихся.
Учитель: существует и обратный способ перевода, предлагая алгоритм перевода десятичного целого числа в двоичную систему счисления.
Приводятся примеры. Сложность перевода для детей в том, что правило деления отличается от математического тем, что при делении чисел требуется определить частное сразу, а не поразрядно. Каждый этап комментируется учителем
Например.
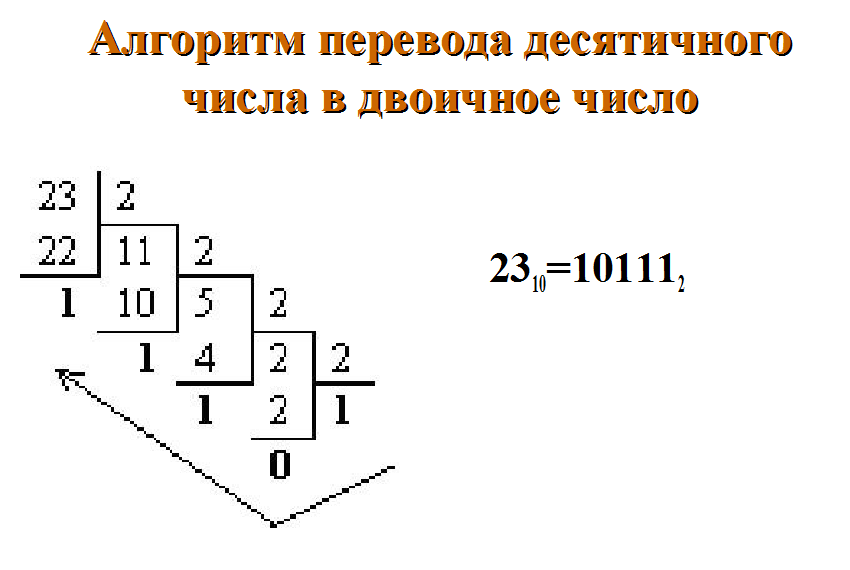
Перевести 2310 в двоичную систему.
Решение. – смотрите документ
Ответ: 101112
5. Решение упражнений.
Затем предлагается самостоятельно перевести числа из десятичной системы в двоичную.
Например, перевести числа 18; 36; 47; 235 и др. из десятичной системы счисления в двоичную систему (с записью в тетрадях).
6. Задание на дом.
Цель: Сообщить учащимся о домашнем задании, разъяснить методику его выполнения и подвести итоги работы.
Задачи: информация о домашнем задании, инструктаж по его выполнению; проверка понимания учащимися содержания работы и способов ее выполнения, подведение итогов урока.
Учитель: На последующих уроках мы продолжим знакомство с системами счисления, а пока дома подумайте и выполните задания:
Переведи в двоичную систему счисления: 345, 125,142
Переведи в десятичную систему счисления: 11111;10101;100011
7.Подведение итогов. Рефлексия.
Цель: дать оценку успешности достижения урока.
Задачи: осознание учениками значимости полученных результатов и готовность использовать их для достижения учебных целей. Стимуляция высказывания личного мнения об уроке и способах работы на нем.
Учитель: Ну а теперь давайте вернемся к задаче и вопросам, поставленным в начале урока. (Учитель снова читает стихотворение А. Старикова)
Учитель: Сколько лет девочке? В какой класс она ходила? Сколько книг в портфеле?
Ученики: 12 лет, 5 класс, 4 книги.
Учитель: Для общения с компьютером нужна двоичная (восьмеричная, шестнадцатеричная) система счисления. В каких (кроме компьютера) приборах (и не только) применяется двоичная система счисления? Оправдано ли это применение (приведите аргументы в защиту).
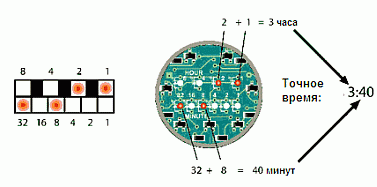
Время в двоичной системе.
В Японии поступили в продажу необычные электронные часы, отображающие время в двоичной системе счисления. (Слайд 7) Выглядят часы также довольно необычно. Они заключены в круглый металлический корпус, однако вместо циферблата со стрелками или индикатора с цифрами под стеклом находится печатная плата зеленого цвета с резисторами, конденсаторами и расположенными в два ряда десятью светодиодами. Именно они и показывают время. Каждый из светодиодов соответствует двоичному разряду. В верхнем ряду имеются четыре диода, соответствующих числам от одного (20) до восьми (23) и показывающих часы. Нижний ряд из шести светодиодов (разряды от 1 до 32) показывает минуты. Чтобы получить нужное значение нужно сложить числа, соответствующие горящим светодиодам. Для удобства владельца рядом со светодиодами указаны числа, которым те соответствуют. Цена часов составляет 8900 иен или около 80 долларов США.
На доске два листочка с оценками урока, прикрепите магнитик на тот листок, который отражает ваше отношение к сегодняшнему уроку.

 Получите свидетельство
Получите свидетельство Вход
Вход



 апример, перевести числа 18; 36; 47; 235 и др. из десятичной системы счисления в двоичную систему (с записью в тетрадях). (Слайд 6)
апример, перевести числа 18; 36; 47; 235 и др. из десятичной системы счисления в двоичную систему (с записью в тетрадях). (Слайд 6) 









 Двоичная система счисления (6.5 MB)
Двоичная система счисления (6.5 MB)
 0
0 2234
2234 284
284 Нравится
0
Нравится
0


