Параллельность прямых в пространстве

МБОУ «Ватинская ОСШ»

Автор: Казиахмедова Разия Керимовна

Содержание

• Взаимное расположение прямых в пространстве
• Параллельные прямые в пространстве
• Теорема о параллельных прямых
• Лемма
• Теорема о параллельности трех прямых
• Взаимное расположение прямой и плоскости в пространстве
• Определение параллельности прямой и плоскости
• Признак параллельности прямой и плоскости
• Свойства параллельных плоскостей (1 ° )
• Свойства параллельных плоскостей (2 ° )
• Признак скрещивающихся прямых
• Теорема о скрещивающихся прямых
• Теорема об углах с сонаправленными сторонами
• Примеры и задачи

Примеры и задачи

• Пример с параллелепипедом
• Задача 1
• Задача 2

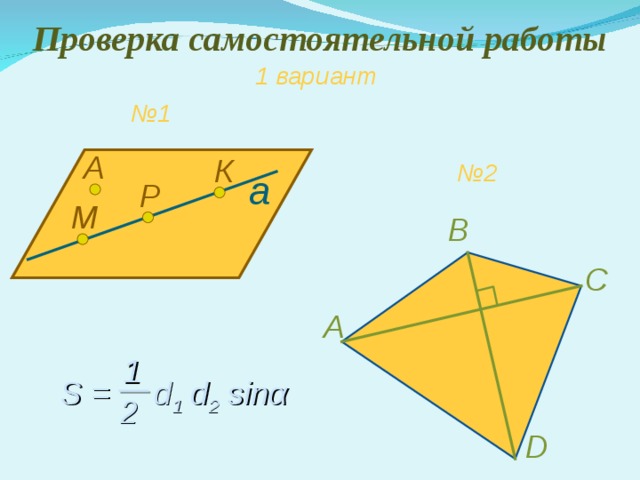
Проверка самостоятельной работы

1 вариант

№ 1

А

К

№ 2

а

Р

M

В

С

А

1

S = d 1 d 2 sin α

2

D

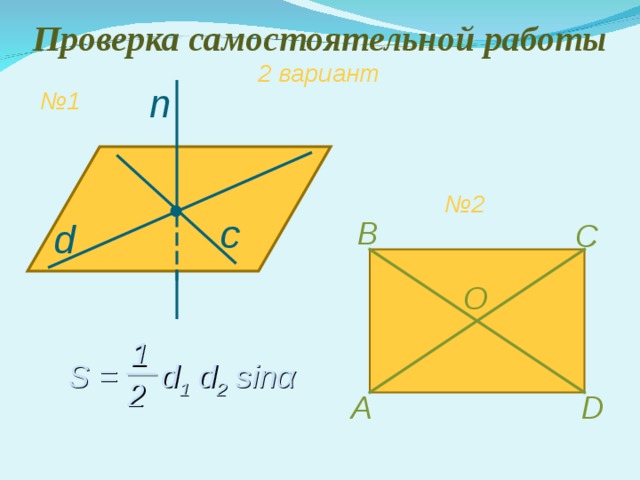
Проверка самостоятельной работы

2 вариант

n

№ 1

№ 2

с

В

d

С

O

1

S = d 1 d 2 sin α

2

D

А

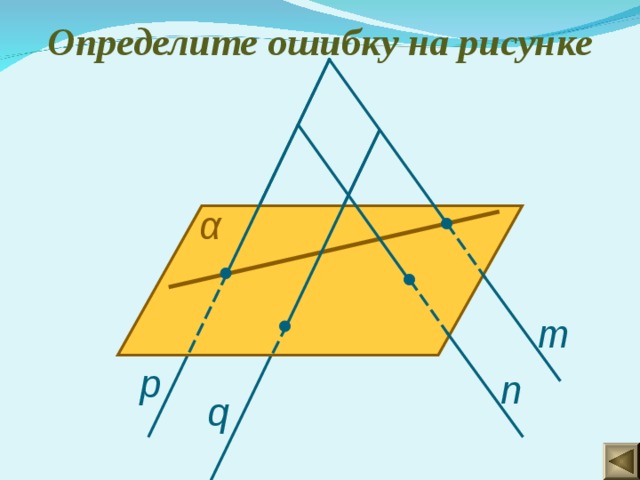
Определите ошибку на рисунке

α

m

p

n

q

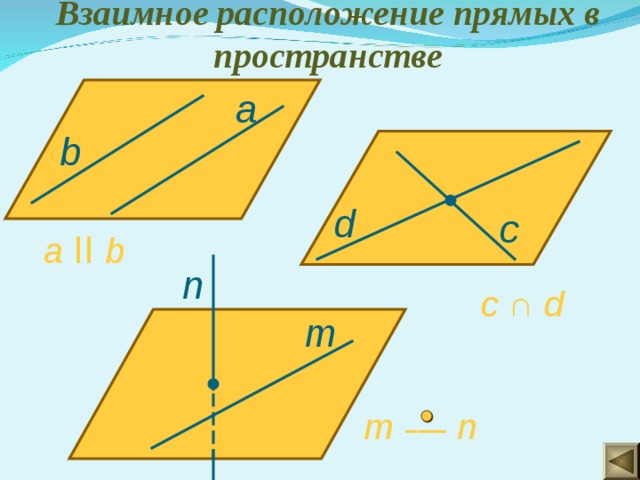
Взаимное расположение прямых в пространстве

а

b

d

с

а ll b

n

c ∩ d

m

m –― n

Параллельные прямые в пространстве

Две прямые называются параллельными ,

если они лежат в одной плоскости и не пересекаются.

α

а

b

а ll b

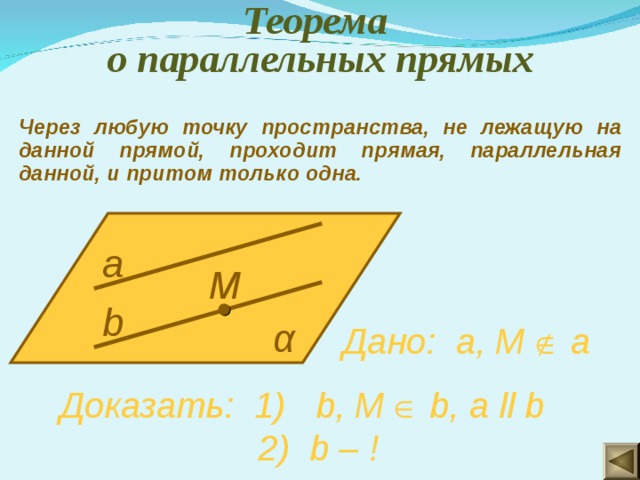
Теорема о параллельных прямых

Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.

а

М

b

α

Дано: а, М  а

Доказать: 1) b , М  b, a ll b

2) b – !

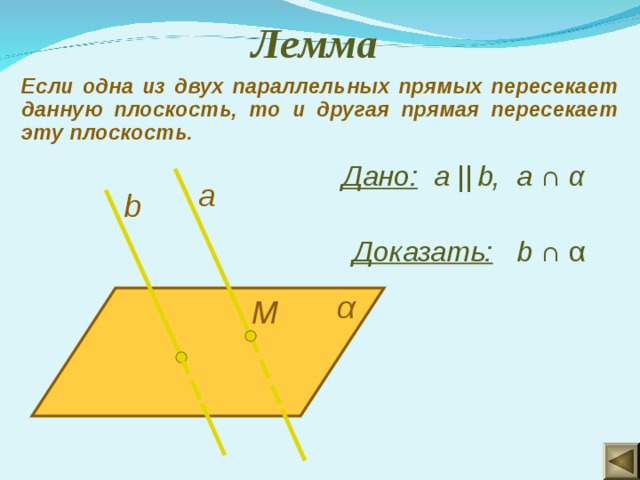
Лемма

Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

Дано: а || b, a ∩ α

a

b

Доказать: b ∩ α

α

M

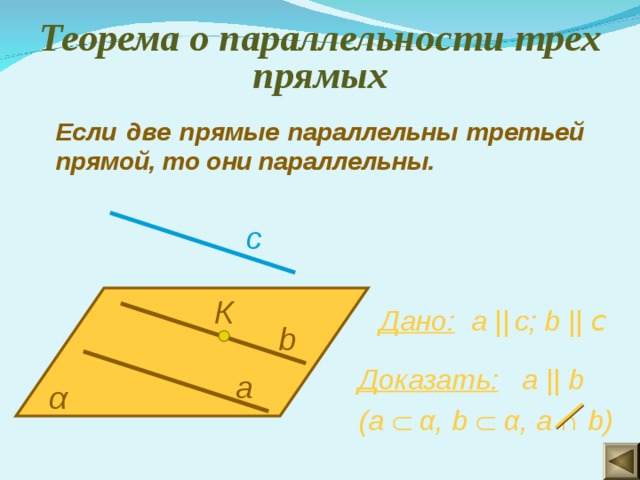
Теорема о параллельности трех прямых

Если две прямые параллельны третьей прямой, то они параллельны.

c

К

Дано: а || c ; b || c

b

Доказать: а || b

(а  α , b  α , a ∩ b)

а

α

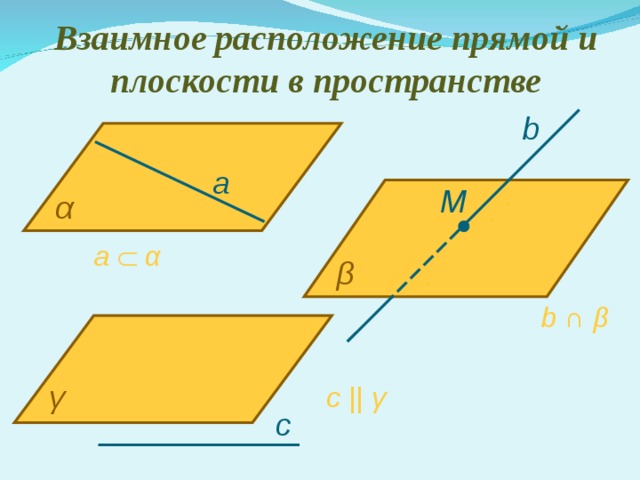
Взаимное расположение прямой и плоскости в пространстве

b

а

М

α

a  α

β

b ∩ β

γ

с || γ

с

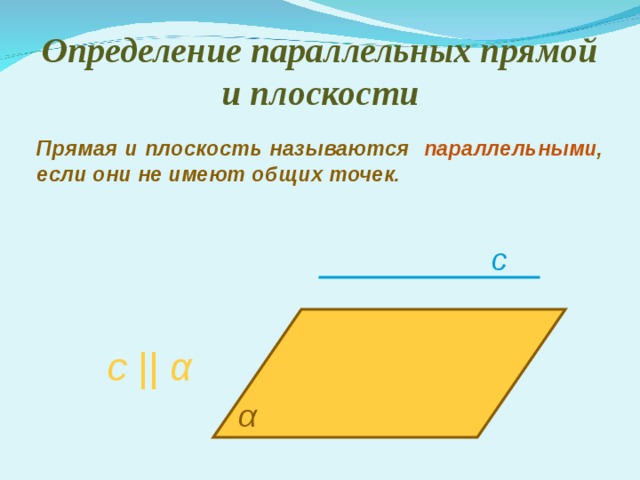
Определение параллельных прямой и плоскости

Прямая и плоскость называются параллельными , если они не имеют общих точек.

c

с || α

α

Пример

B 1

C 1

А 1

D 1

С

В

А

D

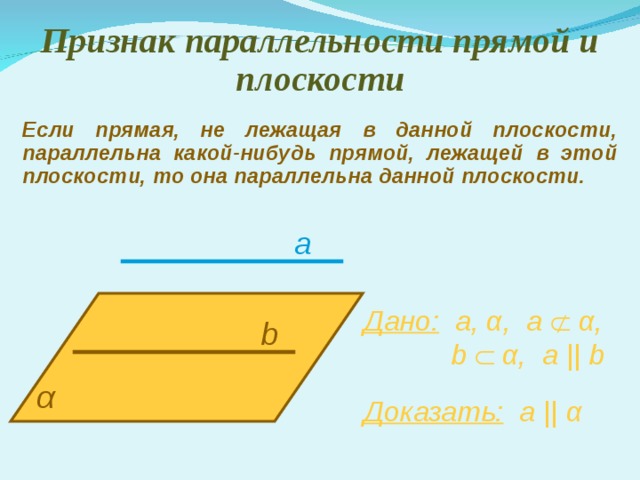
Признак параллельности прямой и плоскости

Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.

a

Дано: а , α , a  α ,

b  α , а || b

b

α

Доказать: а || α

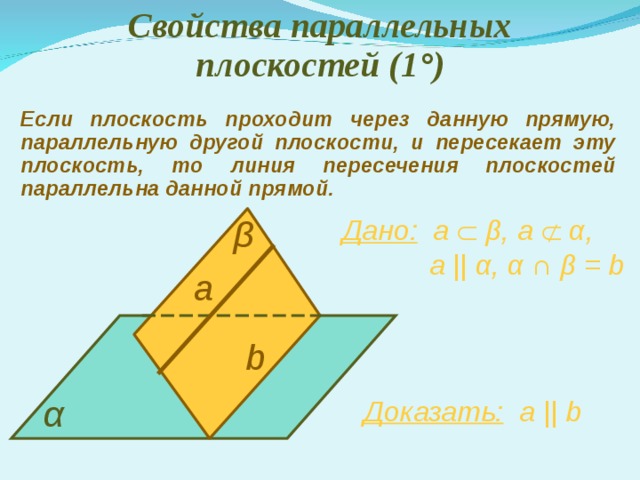
Свойства параллельных плоскостей (1 ° )

Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.

Дано: a  β , a  α ,

а || α , α ∩ β = b

β

а

b

α

Доказать: а || b

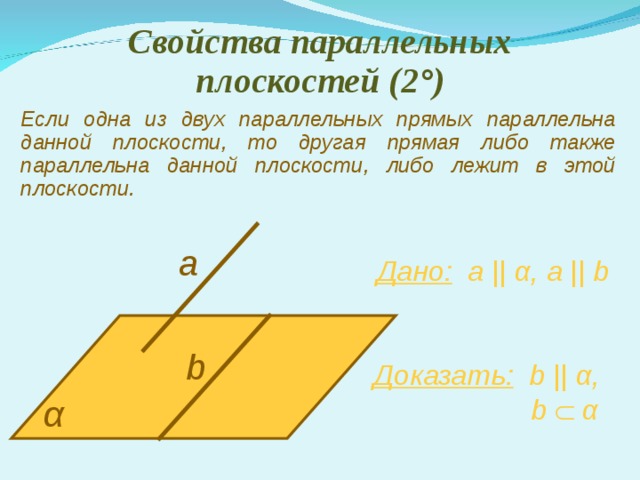
Свойства параллельных плоскостей ( 2° )

Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.

а

Дано: а || α , а || b

b

Доказать: b || α ,

b  α

α

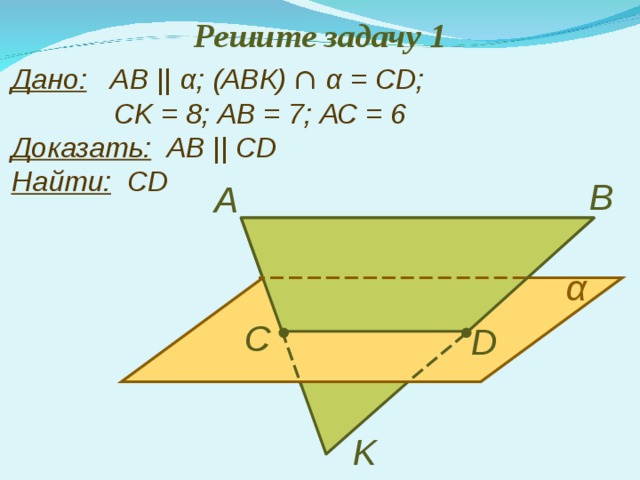
Решите задачу 1

Дано: АВ || α ; (АВК) ∩ α = С D ; С K = 8; АВ = 7; АС = 6 Доказать: АВ || С D Найти: С D

В

А

α

С

D

K

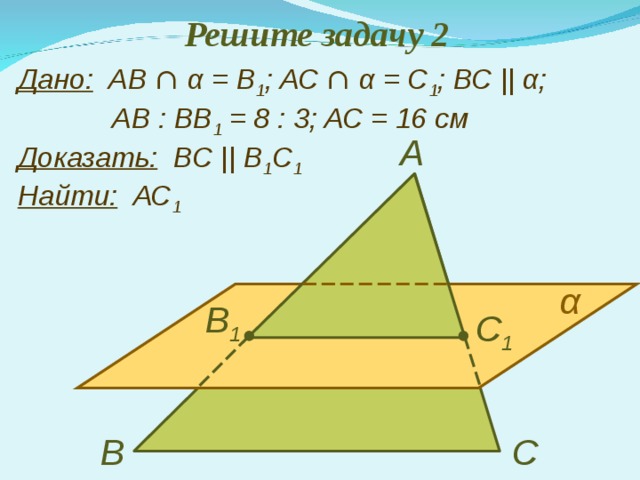
Решите задачу 2

Дано: АВ ∩ α = В 1 ; АС ∩ α = С 1 ; ВС || α ; АВ : ВВ 1 = 8 : 3 ; АС = 16 см Доказать: В C || B 1 С 1 Найти: АС 1

А

α

В 1

С 1

В

С

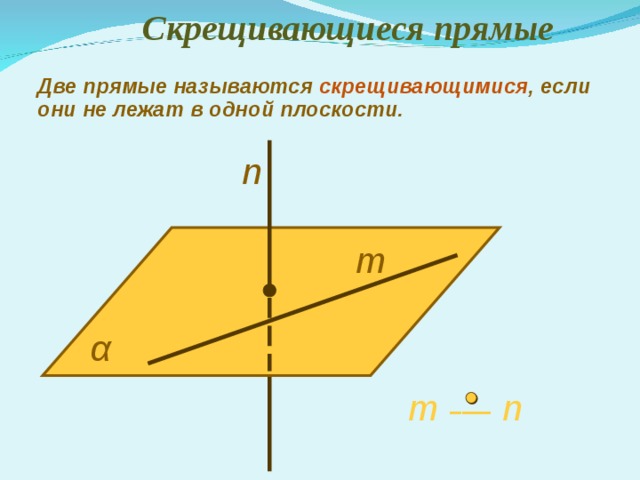
Скрещивающиеся прямые

Две прямые называются скрещивающимися , если они не лежат в одной плоскости.

n

m

α

m –― n

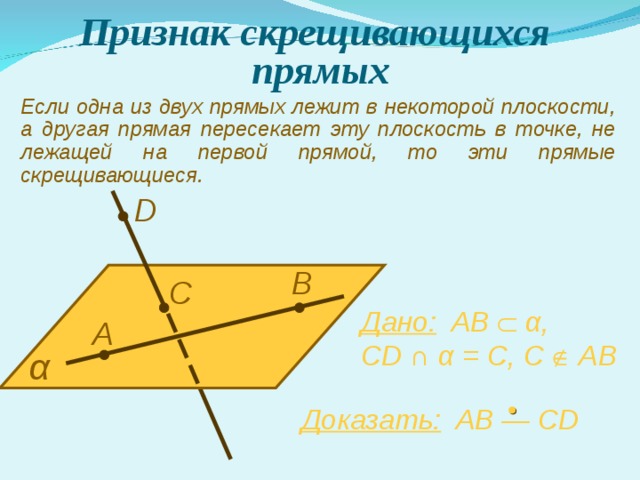
Признак скрещивающихся прямых

Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.

D

В

С

Дано: AB  α ,

CD ∩ α = C, C  AB

А

α

Доказать: AB — CD

Ε

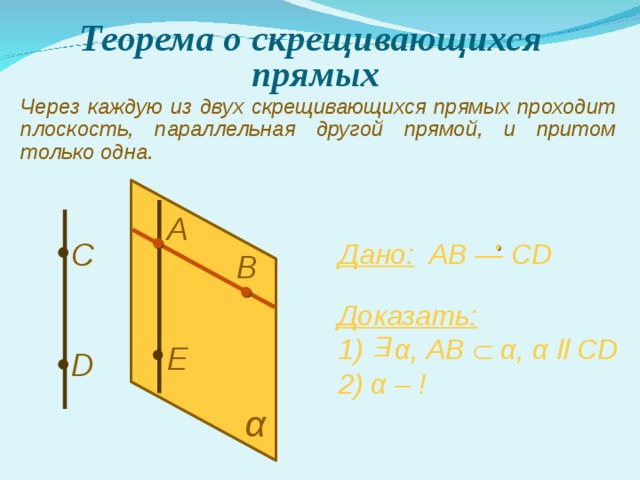
Теорема о скрещивающихся прямых

Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.

А

С

Дано: AB — CD

В

Доказать:

1) α , AB  α , α ll CD

2) α – !

Е

D

α

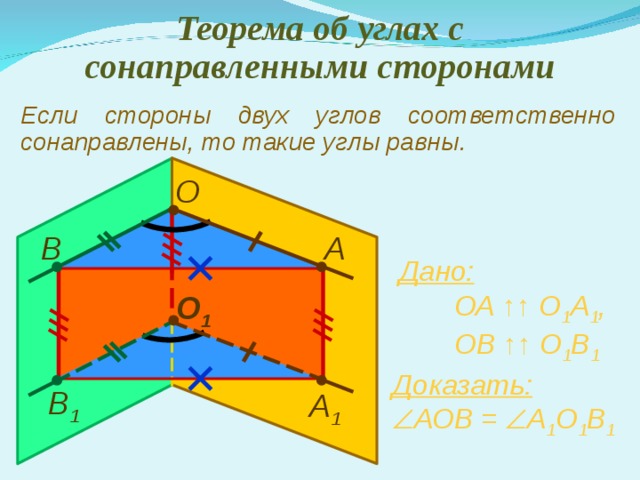
Теорема об углах с сонаправленными сторонами

Если стороны двух углов соответственно сонаправлены, то такие углы равны.

О

А

В

Дано:

ОА ↑ ↑ О 1 А 1 ,

ОВ ↑↑ О 1 В 1

О 1

Доказать:

 АОВ =  А 1 О 1 В 1

В 1

А 1

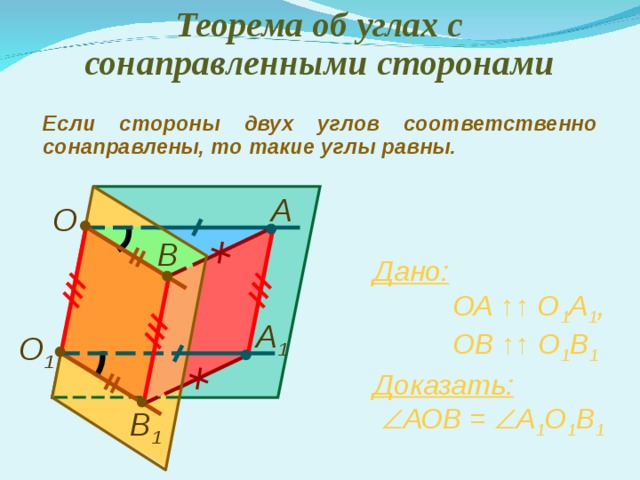
Теорема об углах с сонаправленными сторонами

Если стороны двух углов соответственно сонаправлены, то такие углы равны.

А

О

В

Дано:

ОА ↑ ↑ О 1 А 1 ,

ОВ ↑↑ О 1 В 1

А 1

О 1

Доказать:

 АОВ =  А 1 О 1 В 1

В 1

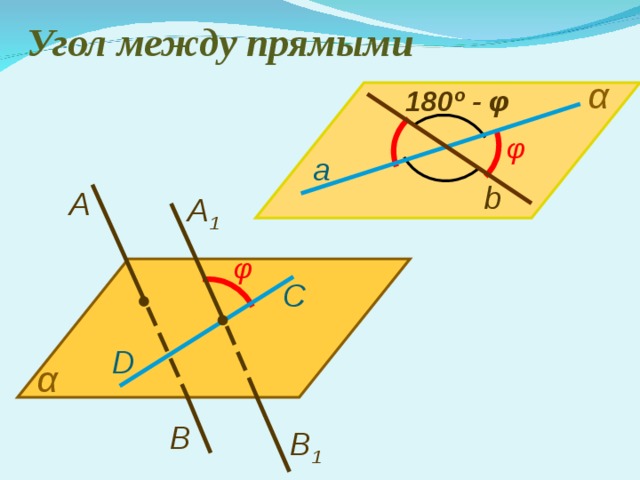
Угол между прямыми

α

180 º - φ

φ

а

b

А

А 1

φ

С

D

α

В

В 1

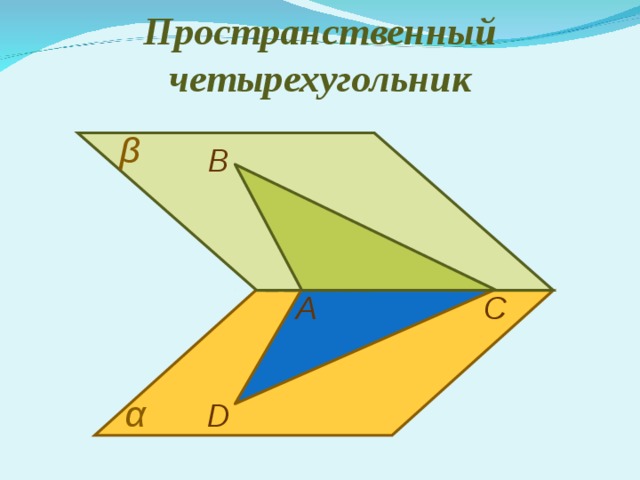
Пространственный четырехугольник

β

В

С

А

α

D

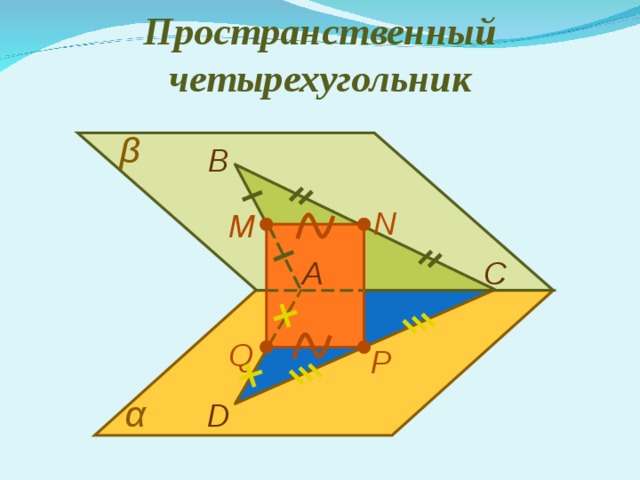
Пространственный четырехугольник

β

В

N

М

С

А

Q

P

α

D

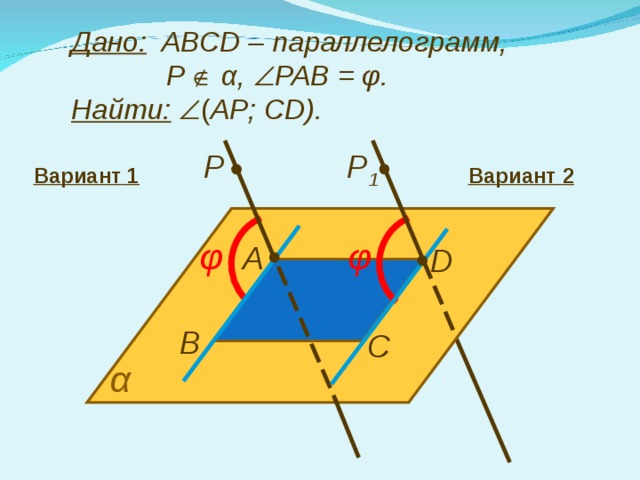
Дано: ABCD – параллелограмм,

Р  α ,  РАВ = φ .

Найти:  ( АР; CD).

P 1

P

Вариант 1

Вариант 2

φ

φ

А

D

В

С

α