Цели:
Сформировать у обучающихся понятие перпендикулярности прямых в пространстве, прямой перпендикулярной плоскости;
изучить лемму о перпендикулярности двух параллельных прямых третьей;
теоремы в которых устанавливается связь между параллельностью прямых и их перпендикулярностью к плоскости.
Продолжить формирование навыков самостоятельности у обучающихся в процессе самоконтроля и при изучении нового материала.
Воспитывать познавательный интерес к предмету.
Ход урока.
1. Орг. момент.
2. Подготовка обучающихся к занятию.
Сообщение темы и цели занятия. Мотивация.
3. Формирование новых знаний.
Работа с обучающимися получившими опережающее задание.
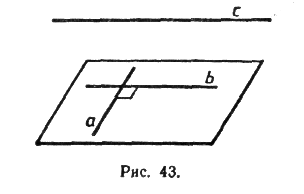
1 обучающийся: Две прямые в пространстве называются перпендикулярными (взаимно перпендикулярными), если угол между ними равен 90°. Перпендикулярность прямых а и b обозначается так: а^b. Перпендикулярные прямые могут пересекаться и могут быть скрещивающимися. На рисунке1 перпендикулярные прямые а и b пересекаются, а перпендикулярные прямые а и с скрещивающиеся.
2 обучающийся: Докажем лемму о перпендикулярности двух параллельных прямых к третьей прямой.
Лемма. Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой.
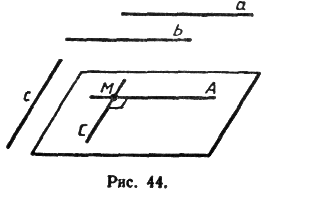
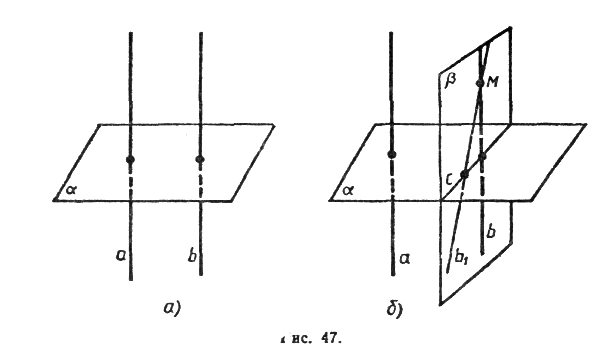
Доказательство. Пусть а||b и a^c. Докажем, что b^с. Через произвольную точку М пространства, не лежащую на данных прямых, проведем прямые МА и МС, параллельные соответственно прямым а и с (рис. 2). Так как a^c, то ÐAMC = 90°.
По условию леммы b||а, а по построению а||МA, поэтому b||МА. Таким образом, прямые b и с параллельны соответственно прямым МА и МС, угол между которыми равен 90°. Это означает, что угол между прямыми b и с также равен 90°, т. е. b^c. Лемма доказана.
Оформление в тетради:
Дано: а||b, a^c
Доказать: b^с

Доказательство:
1. Через точку М Îa, МА|| a, МС|| c, a ^ cÞ ÞМА^МСÞÐAMC=90°.
2. b||а, а||МAÞ b||МАÞ b^c.
3 обучающийся: Параллельные прямые, перпендикулярные к плоскости. Определение. Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.
Перпендикулярность прямой а и плоскости a обозначается так: a^a. Говорят также, что плоскость a, перпендикулярна к прямой а.
Если прямая а перпендикулярна к плоскости a, то она пересекает эту плоскость. В самом деле, если бы прямая а не пересекала плоскость a, то она или лежала бы в этой плоскости, или была бы параллельна ей. Но тогда в плоскости a имелись бы прямые, не перпендикулярные к прямой а, например прямые, параллельные ей, что противоречит определению перпендикулярности прямой и плоскости. Значит, прямая а пересекает плоскость a.
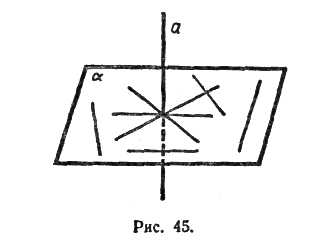
На рисунке 3 изображена прямая а, перпендикулярная к плоскости a.
Окружающая нас обстановка дает много примеров, иллюстрирующих перпендикулярность прямой и плоскости. Непокосившийся телеграфный столб стоит прямо, т. е. перпендикулярно к плоскости земли. Так же расположены колонны здания по отношению к плоскости фундамента, линии пересечения стен по отношению к плоскости пола и т. д.
Докажем две теоремы, в которых устанавливается связь между параллельностью прямых и их перпендикулярностью к плоскости.
Теорема. Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости,
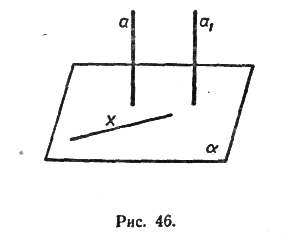
Доказательство. Рассмотрим две параллельные прямые а и a1 и плоскость a, такую, что a^a. Докажем, что и a1^a.
Проведем какую-нибудь прямую х в плоскости a (рис. 4). Так как a^a, то a^x. По лемме о перпендикулярности двух параллельных прямых к третьей a1^x. Таким образом, прямая a1 перпендикулярна к любой прямой, лежащей в плоскости a, т. е. a1^a. Теорема доказана.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход





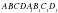 - параллелепипед,
- параллелепипед, 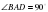
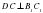 ,
, 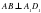

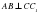 ,
, 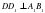











 Конспект урока по математике "Перпендикулярность прямой и плоскости" (0.31 MB)
Конспект урока по математике "Перпендикулярность прямой и плоскости" (0.31 MB)
 1
1 777
777 118
118 Нравится
0
Нравится
0


