Параллельные прямые

Две прямые на плоскости называются параллельными, если они не пересекаются.

Обозначение:

a ║ b

ОСНОВНОЕ СВОЙСТВО

Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.

ТЕОРЕМА 1.1

Если прямая, не проходящая ни через одну из вершин треугольника, пересекает одну из его сторон, то она пересекает только одну из двух других сторон.

Доказательство - смотри презентацию

РЕШЕНИЕ ЗАДАЧ

№1

На стороне BC ∆ABC взята точка D. Найдите угол BAD, если он в 2 раза меньше, чем угол CAD, а уголBAC = 84⁰.

Далее в презентации тест. (Всего презентация содержит 31 слайд).

ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ

Определение, построение, обозначение,

свойство.

Учитель Козина Н.А.

ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ

Определение

Две прямые на плоскости называются параллельными, если они не пересекаются.

ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ

Построение

С помощью угольника и линейки

а

B

b

ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ

Обозначение

a ║ b

a

b

ОСНОВНОЕ СВОЙСТВО IX

Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.

а

B

b

ТЕОРЕМА 1.1

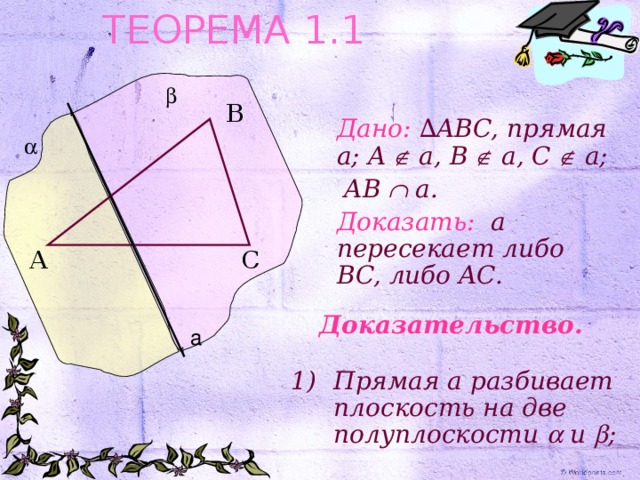
Если прямая, не проходящая ни через одну из вершин треугольника, пересекает одну из его сторон, то она пересекает только одну из двух других сторон.

ТЕОРЕМА 1.1



B

Дано: ∆ ABC, прямая a; A  a, B  a, C  a;

AB  a.

Доказать: a пересекает либо BC, либо AC.



C

A

Доказательство.

a

• Прямая a разбивает плоскость на две полуплоскости  и  ;

ТЕОРЕМА 1.1



B

Дано: ∆ ABC, прямая a; A  a, B  a, C  a;

AB  a.

Доказать: a пересекает либо BC, либо AC.



C

A

Доказательство.

• Пусть A   ;

a

• Т.К. AB  a, то B   ;
• Пусть C   , тогда BC  a, AC  a;
• Пусть C   , тогда AC  a, BC  a.
• Значит, a пересекает либо BC, либо AC.

РЕШЕНИЕ ЗАДАЧ

№ 1

На стороне BC ∆ ABC взята точка D . Найдите  BAD, если он в 2 раза меньше, чем  CAD, а  BAC = 84◦ .

РЕШЕНИЕ ЗАДАЧ

№ 2

∆ DBE = ∆KOP. DE = 4,5 см ; DB = 9 см ;  D = 60◦,  B = 30◦ .

Найдите соответственные стороны и углы ∆ KOP.

ДОМАШНЕЕ ЗАДАНИЕ

Учебник.П11; П12.

Вопросы 27, 28, 29.

Задача №38.

Учить к зачету формулировки основных свойств.

ТЕОРЕМЫ И ДОКАЗАТЕЛЬСТВА

Решение задач.

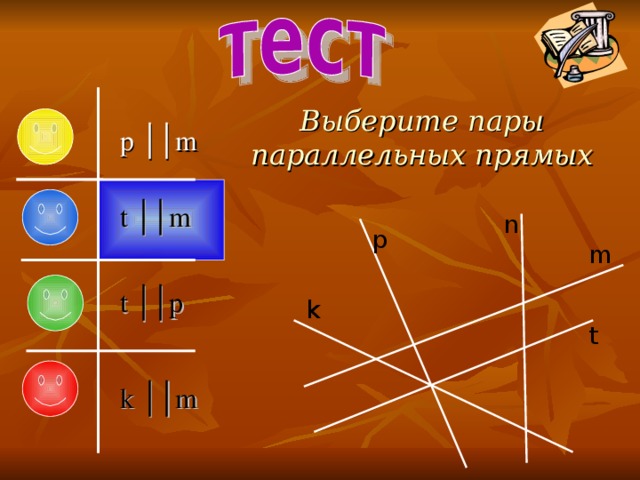
Выберите пары параллельных прямых

p ││m

t ││m

n

p

m

t ││p

k

t

k ││m

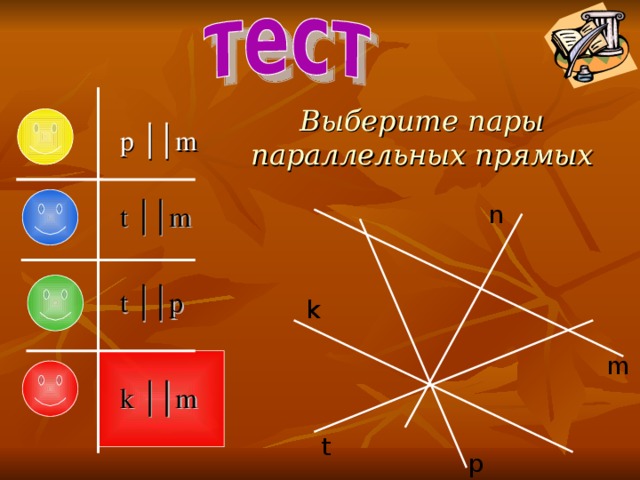
Выберите пары параллельных прямых

p ││m

t ││m

n

t ││p

k

m

k ││m

t

p

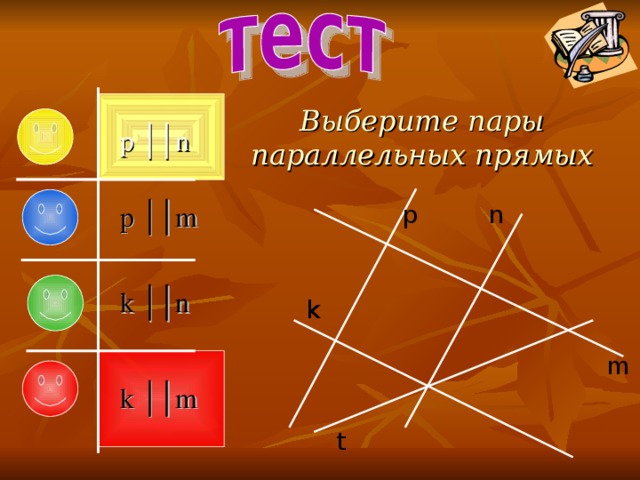
Выберите пары параллельных прямых

p ││n

p

p ││m

n

k ││n

k

m

k ││m

t

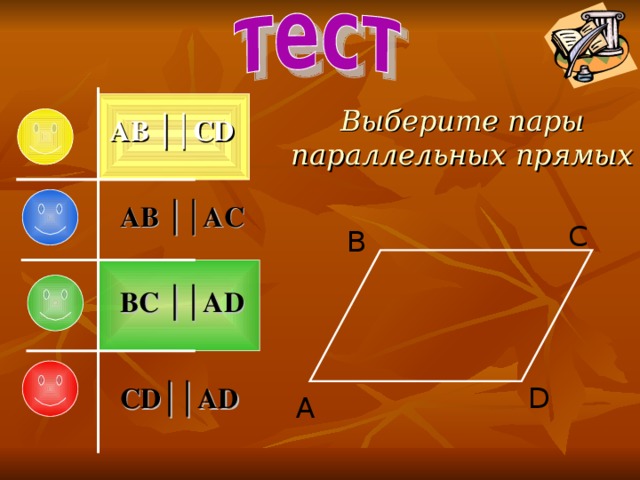
Выберите пары параллельных прямых

AB ││CD

AB ││AC

C

B

BC ││AD

CD ││AD

D

A

РЕШЕНИЕ ЗАДАЧ

№ 1

Могут ли точки A,B и M лежать на одной прямой, если AB = 20 см; BM = 8,3 см ; AM = 12,7 см.

РЕШЕНИЕ ЗАДАЧ

№ 2

Прямой угол MKC разделен лучом KB на 2 угла. Один из них на 38 ° больше другого. Найдите градусные меры полученных углов.

РЕШЕНИЕ ЗАДАЧ

№ 3

Точка K лежит между точками E и F, причем EF = 8,7 см; KE = 3,9 см.

Найдите расстояние

между точками K и F .

ДОМАШНЕЕ ЗАДАНИЕ

Задачи.

• ∆ MPT = ∆ABK. MP = 7 см ;  B = 40°. Найти AB и  P .
• Точка O лежит между точками B и M . OB = 8 см ; OM = 17,2 см. Найти расстояние между точками B и M .
• Прямой угол CDF разделен лучом DK на 2 угла. Один из них на 18 ° меньше другого. Найти градусные меры полученных углов.

• На каком рисунке a ║ b ?

a

a

a

b

a

b

b

b

АКСИОМЫ

Решение задач

РЕШЕНИЕ ЗАДАЧ

№ 1

Луч OM проходит между сторонами угла AOD . Найдите  AOM и  MOD, если  AOM составляет две третьих от  MOD.  AOD = 140°.

РЕШЕНИЕ ЗАДАЧ

№ 2

∆ AOB = ∆MKP;

AO = 5 см ;  K = 67°;

Найти MK и  O.

РЕШЕНИЕ ЗАДАЧ

№ 3.

Могут ли точки E, F, D лежать на одной прямой, если EF = 22 см ;

FD = 7,3 см ;

ED = 15,7 см.

ДОМАШНЕЕ ЗАДАНИЕ

• ∆ PQR = ∆AMB; MB = 8 см ;  R = 120°. Найти QR;  B.
• Точка K лежит между точками M и F, причем MF = 30 см ; KF = 24 см . Найти расстояние между точками K и M.
• Угол MBC, равный 124 ° , разделен лучом BD на два угла. Один из них в 3 раза больше другого. Найдите градусные меры полученных углов.

• На каком рисунке a  b ?

a

a

a

b

a

b

b

b

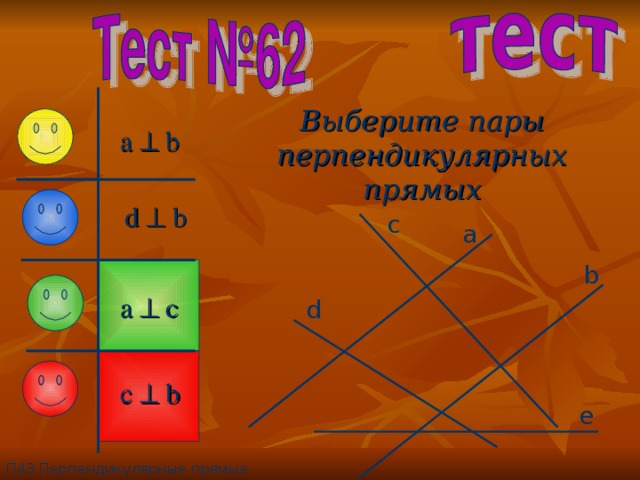
Выберите пары перпендикулярных прямых

a  b

d  b

c

a

b

a  c

d

c  b

e

П4 3 Перпендикулярные прямые

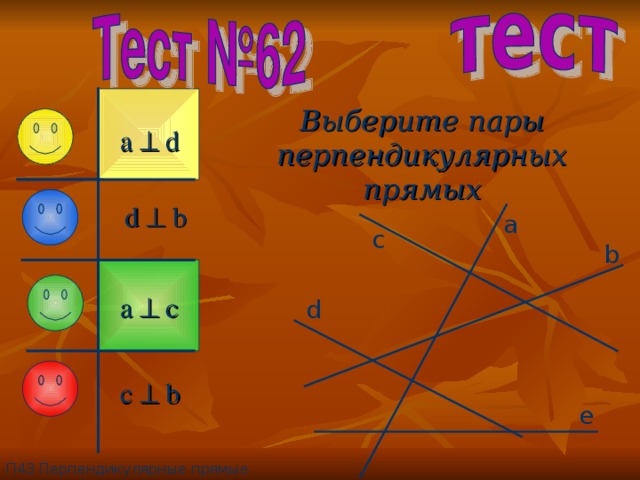
Выберите пары перпендикулярных прямых

a  d

d  b

a

c

b

a  c

d

c  b

e

П4 3 Перпендикулярные прямые

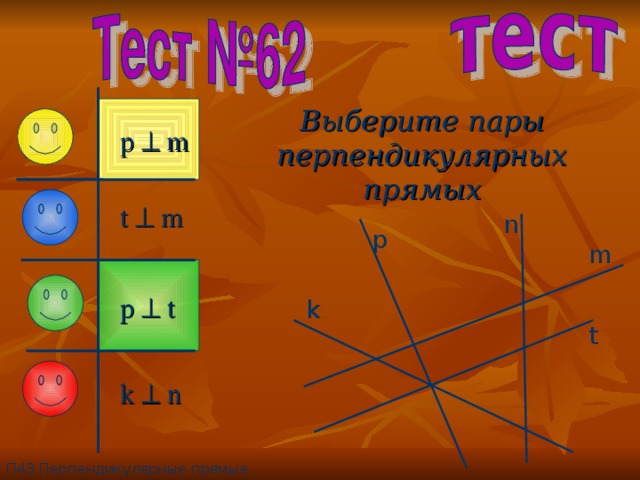
Выберите пары перпендикулярных прямых

p  m

t  m

n

p

m

p  t

k

t

k  n

П4 3 Перпендикулярные прямые

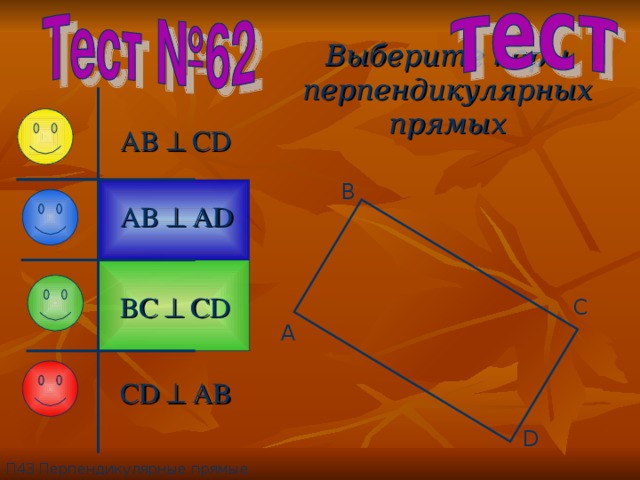
Выберите пары перпендикулярных прямых

AB  CD

B

AB  AD

BC  CD

C

A

CD  AB

D

П4 3 Перпендикулярные прямые