«Многочлен и его стандартный вид»

Тема урока:

«Многочлен и его стандартный вид»

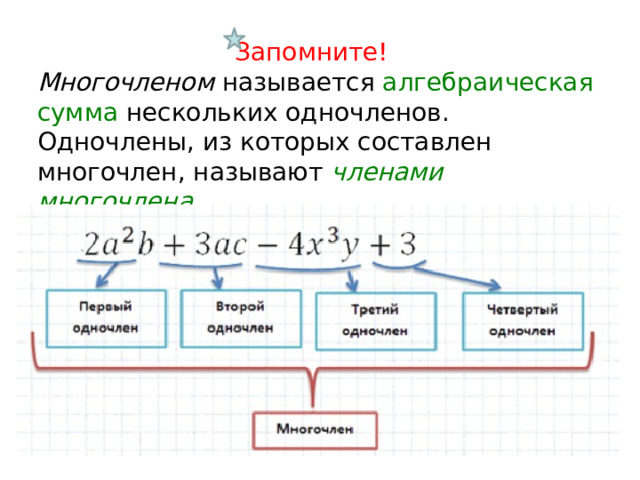
Запомните!

Многочленом   называется   алгебраическая сумма   нескольких одночленов.

Одночлены, из которых составлен многочлен, называют   членами многочлена .

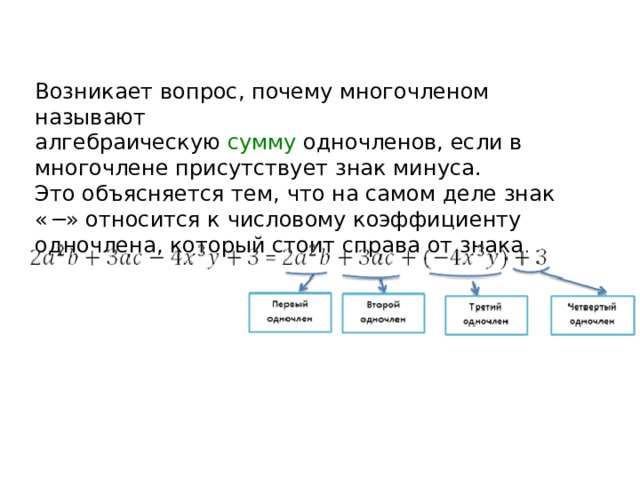
Возникает вопрос, почему многочленом называют алгебраическую  сумму  одночленов, если в многочлене присутствует знак минуса.

Это объясняется тем, что на самом деле знак « − » относится к числовому коэффициенту одночлена, который стоит справа от знака .

Являются многочленами

5а 2 в+2+4ав 2 -14а 3 ;

21а 8 +2ав 2 ;

16а 4 – 4а 2 в 2 + 15ав 3 ;

4х 2 у – 5ху;

Трехчлены

(трином)

Двучлены

(бином)

3х

Одночлены

НЕ ЯВЛЯЮТСЯ МНОГОЧЛЕНАМИ

4с 2 – 5а : с 3 ; (14 x 4 – 5x 2 ) : у + 3ху 2 : у 7 – 8.

Важно!

Подобными одночленами называют одночлены,

у которых одинаковый состав букв и их степеней.

Многочлен, состоящий из одночленов стандартного вида, среди которых нет подобных, называют многочленом стандартного вида.

Как привести многочлен к стандартному виду

Запомните!

Чтобы   привести многочлен к стандартному виду , нужно:

• Привести каждый одночлен многочлена к стандартному виду.

• Выполнить приведение подобных одночленов.

Запомните!

Степенью многочлена называют  

наибольшую   из степеней входящих

в него одночленов.

Приведем подобные члены в многочлене :

15а 2 в + 3 + 4ав 2 – 3а 2 в – 7

Группируем подобные члены (слагаемые)

Упрощаем

Можно проще:

8

Приведем подобные члены в многочлене :

а) 10х – 8ху - 3ху =

– 8ху

- 3ху

б) 2 ab – 7ab + 7a 2 =

2 ab

– 7ab

3 х 4

– 8 х 4

в) 3 х 4 – 5x + 7x 2 – 8 х 4 +5x=

г) 2 a 3 + a 2 – 17 – 3a 2 +a 3 – a – 80 =

2 a 3

– 3a 2

a 2

a 3

– 17

– 80

8