ХХ век – век инновационных технологий, который требует технологизацию учебного процесса. Современная педагогика в этом плане развивается в активном, интерактивном и конструктивном направлении. При сравнении конструктивного подхода к обучению с традиционной формой передачи знаний нетрудно заметить, что процесс построения новых знаний происходит на основании предыдущих знаний и умений. В этом процессе знания учащихся находятся в движении, они могут легко превращаться в новые знания, путем добавления одного элемента. Последовательно построенные новые знания, интегрируясь с предыдущими и последующими знаниями, создают целостную картину действий. Интерактивная учебная деятельность учащихся совмещенная с мыслительной деятельностью приводит к формированию оперативности мышления, результатом которого является преобразование одних знаний в новые знания.
Термин «инновация» как вид педагогической деятельности означает внесение в учебный процесс нового (факты, метода, приемы), улучшающего действующую систему образования.
Известны имена и заслуги трех групп педагогов-новаторов, создавших методические системы и авторские школы. В начале XX века, это – М. Монтессори, С. Френе. Д. Дьюи, Г. Кершенштейнер, Я. Корчак, Р. Штейнер, С.Т. Шацкий, М.М. Пистрак, А.С. Макаренко и др.
В середине XX века, это – В. А. Сухомлинский, Ш.А. Амонашвили, Л.В. Занков, В. В. Давыдов, С.Н. Лысенкова, И. П. Иванов, Б. П. Никитин, М. П. Щетинин, А.Н. Тубельский, И. П. Раченко и др.
В конце XX века, это – Ю.А. Конаржевский, О.С. Саметис, Г. Г. Габдуллин, И.К. Шалаев, В. Ф. Шаталов, И. П. Волков, В. К. Дьяченко, Г. Лозанов, Ф.Д. Бунятова, П. М. Эрдниев, Е. Н. Ильин и др.
Конструктивное обучение нацелено на развитие познания, на построения учащимися своих знаний на основе имеющихся знаний и опыта. Здесь в основном делается упор не на память, а на мышление. Конструктивное обучение считается наиболее важным и актуальным из технологий обучения современного общества, т.к. в процессе обучения оно повышает мышление ученика и развивает его. Сам по себе – это стиль и создание знаний. Эта теория органически охватывает все достижения предыдущих этапов активизации учебного процесса и развития конструктивного мышления всех его участников. Урок состоит из двух частей.
Часть I:
В этой части я работаю с классом над поставленными вопросами. Здесь моей целью является определить уровень понимания учащимися темы, расширить и углубить эти понимания новыми знаниями. Ученики же работая над выстроенными знаниями путем логической установки учителя, преобразовывают их в новые знания, более высокого уровня.
Это часть проводиться в форме активного обсуждения решаемых примеров.
Часть II:
Во второй части урока, ученики, работая в командах, применяют приобретенные знания в рабочих листах, подготовленных мною заранее.
Цель этой части укрепить умения и навыки, применение новых знаний.
После выполнения заданий на рабочих листах каждая команда выбирает лидера для презентации работ. При презентации работ я делаю установку на оценивание выполненных заданий самими командами, привлекая внимание учеников на обсуждение. После контроля и оценивания результатов работы и заданий на дом, благодарю всех за сотрудничество.
Конспект урока:
Цели:
- Обеспечить усвоение учащимися знаний по умножению одночлена на многочлен
- Развить познавательное умение и правильное применение этих знаний учащимися на практике
- Работа в командах: Формирование у учащихся стремления к совершенствованию знаний, слушать друг друга, умение анализировать, логически мыслить, прийти к общему мнению.
I часть урока:
Ключевое слово: умножение.
Давайте решим следующие примеры:
-7a2b3c ∙ 4a2b4=…
Через минуту команды уже готовы ответить. Правильный ответ высвечивается на экране. Ответ: -7 ∙ 4 ∙(a2 ∙ a2) ∙(b3 ∙b4) ∙c= -28a4b7c
Решим следующий пример:
-1/7x3y ∙ 4x2y3 ∙ (-21xy6)=…
В течении минуты команды подготавливают ответ. Затем правильный ответ появляется на экране. Ответ: -1/7 ∙(-21)∙4∙(x3∙x2∙x)∙(y∙y3y6)=12x6y10
Сразу после решения примеров начинаем обсуждение.
Вопросы к классу:
В. Как вы решили эти примеры? Какие правила вы при этом использовали?;
О. Сначала мы умножили числовые множители, а затем степени с одинаковыми основаниями;
О. Мы использовали правило умножения одночленов;
В. Как, по-вашему, что при этом получается?;
О. При этом получается одночлен, потому что произведение одночленов есть одночлен;
О. Мы, упростив, получили стандартный вид одночлена;
В. Что значить «стандартный вид» одночлена?;
О. Это – когда в одночлене число и каждая переменная записаны один раз в определенной степени;
В. Вы сказали: «мы упростили», а как? Какие законы вы при этом использовали?;
О. Переместительный закон умножения: ab = ba. Используя его, мы меняли местами сомножителей;
О. Сочетательный закон умножения: (ab)∙c=a∙(bc). Он был использован во втором примере, когда мы сочли нужным написать рядом -1/7 ∙(-21), чтобы потом их сократить.
Решим еще два примера.
- (-3a3b2)3=…
Через минуту команды готовы ответить. Затем правильный ответ появляется на экране:
(-3)3∙(a3)3∙(b2)3=-27a9b6
- (-1/2 x3y2)4=…
После решения команд правильный ответ выводится на экран. Ответ:
(-1/2)4∙(x3)4∙(y2)4=1/16x12y8
В. Как вы нашли ответ?;
О. Мы возвели в степень сначала числовой множитель, затем каждую степень из множителей тоже возвели в степень;
В. А что в результате получился?;
О. Одночлен, потому что степень одночлена тоже одночлен;
В. Как вы считаете, что нам необходимо знать и уметь делать при решении таких примеров?;
О. Надо знать правило умножения одночленов и возведения их в степень;
О. Уметь применять эти правила при выполнении подобных примеров;
Поупражняемся еще.
Давайте применим наши знания для более сложного задания:
Возьмем одночлен -5b и умножим его на многочлен 2b6-4b+7.
В ходе решения команды приходят к правильному ответу.
-5b∙(2b6-4b+7)=-5b∙2b6-5b∙(-4b)+(-5b)∙7=-10b7+20b2-35b
Ответ готов, показываем слайд с готовым ответом.
Следующий пример:
Берем одночлен 8а2 и умножаем его на многочлен 5b3+2a-3ab
Когда у команд готов правильный ответ показываем слайд с готовым ответом:
8a2∙ (5b3+2a-3ab)=8a2∙5b3+8a2∙2a-8a2∙3ab=40a2b3+16a3-24a3b
В. Каким образом вы получили ответ?;
О. В каждом примере мы умножили одночлен, который стоял перед скобкой, на каждый член многочлена в скобке;
В. Что у вас получилось?;
О. Сложив и упростив эти одночлены, мы получили многочлен в стандартном виде;
В. Что же является многочленом? И что означает «Многочлен в стандартном виде»?;
О. Сумму одночленов называют многочленом;
О. Если каждый член многочлена является одночленом стандартного вида и многочлен не содержит подобных слагаемых, то говорят, что он записан в стандартном виде;
В. Какое свойство умножения было применено?;
О. При раскрытии скобок, мы использовали распределительное свойство умножения; a(b+c)=ab+ac
В; Какие правила раскрытия скобок вы знаете?;
О. Если перед скобкой стоит знак «+», то скобки опускаются, а члены записываются с теми же знаками; a+(b+c)= a+b+c
О. Если перед скобкой стоит знак «-», то скобки опускаются, а члены записываются с противоположными знаками; a-(b+c)=a-b-c
Давайте, используя эти правила решим уравнение:
3(х-1)-2(3-7х)=2(х-2)
Когда предполагаемый ответ готов, показываю слайд:
3х-3-6+14х=2х-4
17х-9=2х-4
17х-2х=-4+9
15х=5
х=5/15
х=1/3
Ответ: х=1/3
И так, чтобы умножить одночлен на многочлен, надо умножать этот одночлен на каждый член многочлена и полученные произведения сложить:
а (b+c)=ab+ac
А теперь попробуйте решить уравнение:
2х2+5х=0
Через минуту предполагаемый ответ готов, показываю слайд:
Выносим за скобки общий множитель (последующая тема):
х∙(2х+5)=0
По условию равенства нулю произведения имеем:
х=0 или 2х+5=0
2х=5
х=-2,5.
Ответ: х=0;-2,5.
Таким образом, вы использовали обратное действие, то есть вынесли общий множитель за скобки и использовали при этом правило:
ab+ac=a(b+c)
II-часть урока:
«Мало иметь хороший ум, главное - уметь его применять».
Словами великого французского математика Рене Декарта начинаем работу в командах.
Каждой команде задается по 7 заданий в заранее подготовленных рабочих листах. – смотри документ.
Время идет, на экране появляется цитата великого Леонардо да Винчи «Единственным критерием истины является опыт».
Время закончилось.
Все команды готовы к обсуждению.
Помогаю прикрепить красочно оформленные листы к доске. Идет бурное обсуждение. Лидер каждой команды выступив, старается оценить работу своей команды на «5», при этом учитываются обнаруженные ошибки и т.д. Таким образом, учащиеся выступают активными субъектами процесса познания.
После контроля и оценивания результата работ и заданий на дом, хвалю и благодарю каждого.
Урок заканчиваю словами выдающегося математика М. В. Ломоносова:
«Математику только затем учить надо, что она ум в порядок приводит».
P.S.: Как видно в этом конструктивном учебном процессе не было передачи готовых знаний. Знания были созданы учениками в процессе мыслительной деятельности, путем логических установок и вопросов учителя, в активной дискуссии.

 Получите свидетельство
Получите свидетельство Вход
Вход



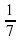 x3y ∙ 4x2y3 ∙ (-21xy6)=…
x3y ∙ 4x2y3 ∙ (-21xy6)=…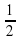 x3y2)4=…
x3y2)4=…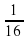 x12y8
x12y8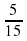
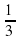
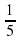 (25x2-15x3+5)=5x2…
(25x2-15x3+5)=5x2…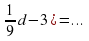









 Произведение одночлена и многочлена. Умножение одночлена на многочлен (40.79 КB)
Произведение одночлена и многочлена. Умножение одночлена на многочлен (40.79 КB)
 1
1 1320
1320 237
237 Нравится
0
Нравится
0


