1. Задачи на раскрашивание шахматной доски
Задача 1. Художник-авангардист Змий Клеточкин покрасил несколько клеток доски размером 88, соблюдая правило: каждая следующая закрашиваемая клетка должна соседствовать по стороне с предыдущей закрашенной клеткой, но не должна — ни с одной другой ранее закрашенной клеткой. Ему удалось покрасить 36 клеток. Побейте его рекорд!
Решение: Можно закрасить 42 клетки, закрасить 43 клетки невозможно. Примеры ответов изображены на рис.1 а,б.
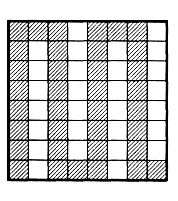

а) б)
Рис. 1
Задача 2. Поля клетчатой доски размером 88 будем по очереди закрашивать в красный цвет так, чтобы после закрашивания каждой следующей клетки фигура, состоящая из закрашенных клеток, имела ось симметрии. Покажите, как можно, соблюдая это условие, закрасить: а) 26; б) 28 клеток. (В качестве ответа расставьте на тех клетках, которые должны быть закрашены, числа от 1 до 26 или до 28 в том порядке, в котором проводилось закрашивание.)
Решение: рис.2.


Рис. 2 Рис. 3
Задача 3. Отметьте на доске 88 несколько клеток так, чтобы любая (в том числе и любая отмеченная) клетка граничила по стороне ровно с одной отмеченной клеткой.
Решение: рис.3.
Задача 4. В квадрате 77 клеток закрасьте некоторые клетки так, чтобы в каждой строке и в каждом столбце оказалось ровно по три закрашенных клетки.
Решение: рис.4 а,б.

а) б)
Рис. 4
При решении задач на раскрашивание шахматной доски нет какого-то определенного используемого математического метода, нужно просто быть внимательным при решении, чтобы учесть все содержащиеся в условии задачи ограничения.
2. Задачи на разрезание шахматной доски
Среди математических задач и головоломок о шахматной доске наиболее популярны задачи на разрезание доски.
Задача 5. Разрежьте изображённую на рисунке 5,а доску на 4 одинаковые части, чтобы каждая из них содержала 3 заштрихованные клетки.
Решение: рис.5,б.
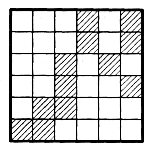

а) б)
Рис. 5
Задача 6. Четыре алмаза.
Один восточный властелин был таким искусным игроком, что за всю жизнь потерпел всего четыре поражения. В честь своих победителей, четырех мудрецов, он приказал вставить в его шахматную доску четыре алмаза – на те поля, на которых был заматован его король (рис.6, где вместо алмазов изображены кони).
После смерти властелина его сын, слабый игрок и жестокий деспот, решил отомстить мудрецам, обыгравшим его отца. Он велел разделить им шахматную доску с алмазами на четыре одинаковые по форме части так, чтобы каждая заключала в себе по одному алмазу. Хотя мудрецы выполнили требование нового властелина, он все равно лишил их жизни, причем, как гласит легенда, для казни каждого мудреца использовал его часть доски с алмазом.
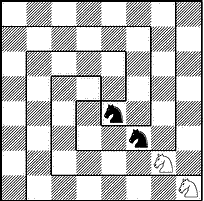
Рис. 6
Условие задачи: Разрезать доску на четыре одинаковые части (совпадающие при наложении) так, чтобы на каждой из них оказалось по одному коню. Предполагается, что разрезы проходят только по границам между вертикалями и горизонталями доски.
Решение: Одно из решений задачи представлено на рис.6. Располагая четырех коней на различных полях доски, можно получить множество задач о разрезании. Интерес в них представляет не только нахождение одного необходимого разреза, но и подсчет числа всех способов разрезать доску на четыре одинаковые части, содержащие по одному коню. Установлено, что наибольшее число решений (800) задача имеет при расположении коней в углах доски.
Задача 7. На какое максимальное число частей можно разрезать шахматную доску, если считать разными части, отличающиеся своей формой или цветом полей при совмещении.

а) б)
Рис. 7
Решение: Максимальное число частей равно 18. На рис.7 представлены два разреза. Решение на рис.7,а принадлежит Лойду; особенность его состоит в том, что одна из частей содержит восемь полей (максимум). В решении на рис.7,б, отличающемся внешней симметрией, ни одна часть не содержит более пяти полей. На рис.7,а части 17 и 18, или 8 и 9, хотя и имеют одинаковую форму, отличаются цветом полей при совмещении. Другие части, например, 3 и 6, вообще не могут быть совмещены (переворачивать их нельзя).
Задача 8. Какое максимальное число полей доски можно пересечь одним разрезом?
Решение: Поля доски образуются в результате пересечения 18 прямых – девяти вертикальных и девяти горизонтальных. С каждой из них прямая-разрез может пересечься лишь в одной точке, но из четырех прямых, образующих края доски, она пересекается лишь с двумя. Отсюда следует, что наша прямая пересекает прямые, образующие поля доски, самое большее в 16 точках. Эти точки разбивают прямую не более чем на 15 отрезков, каждый из которых заключен внутри какого-нибудь поля. Таким образом, любой разрез доски пересекает не более 15 полей. Из рис.8 следует, что ровно столько полей пересекает разрез, проведенный параллельно диагонали доски и проходящий через середины сторон двух угловых клеток.
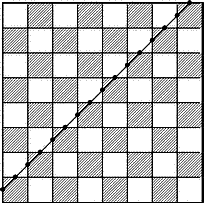

Рис. 8 Рис. 9
Задача 9. Сколько нужно провести разрезов на доске, чтобы пересечь все ее поля?
Решение: Семь прямых могут пересечь все 64 поля доски. Для этого одну прямую нужно провести почти в диагональном направлении через центр доски, а шесть других – в направлениях почти параллельных второй диагонали доски (рис.9).
3. Шахматная доска и домино
Задачи про шахматную доску и домино можно считать частным случаем задач на разрезание доски.
Задача 10. Можно ли целиком покрыть домино квадрат 88, из которого вырезаны противоположные угловые клетки (рис. 10,а)?
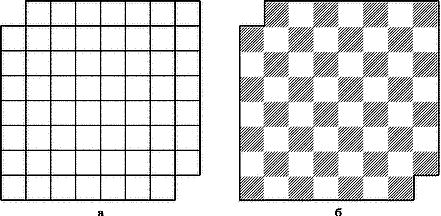
a) б)
Рис. 10
Решение: Предполагается, что каждое домино имеет размеры 21 и покрывает два соседних поля доски, а каждое поле покрывается одной половинкой домино. Можно было бы заняться алгебраическими рассуждениями, но шахматное решение гораздо проще. Окрасим урезанный квадрат в черно-белый цвет, превратив его в шахматную доску без двух угловых полей a8 и h1 (рис.10,б). При любом покрытии доски каждое домино покрывает одно белое и одно черное поле. У нас же черных полей на два больше, чем белых, и поэтому необходимого покрытия не существует! Таким образом, раскраска доски не только позволяет шахматисту легче ориентироваться во время игры, но и служит средством решения математических головоломок.
Задача 11. Пусть на шахматной доске вырезаны два поля разного цвета. Всегда ли можно покрыть оставшуюся часть доски 31 домино?
Решение: Оказывается, что всегда. Проведем замкнутую линию, как показано на рис.11. Если из доски вырезаны соседние поля, то разорванная линия будет состоять из одного куска, проходящего через 62 поля, при этом цвета полей чередуются. Если мы станем размещать домино вдоль этой линии, то закроем всю оставшуюся часть доски. Если вырезанные поля не являются соседними, то линия разорвется на две части, проходящие через четное число полей, и каждую из них можно покрыть домино.
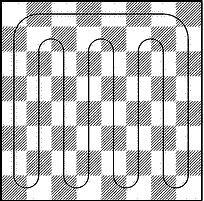
Рис. 11
Задача 12. Пусть из шахматной доски вырезано некоторое количество полей. При каком наименьшем числе таких полей на оставшуюся часть доски нельзя поместить ни одного домино?
Решение: Достаточно вырезать из доски 32 поля одного цвета – либо белые, либо черные, и на ней не останется места ни для одного домино.
Задача 13. Можно ли покрыть шахматную доску 21 прямым тримино и одним мономино? Если можно, то какие поля занимает при этом мономино?
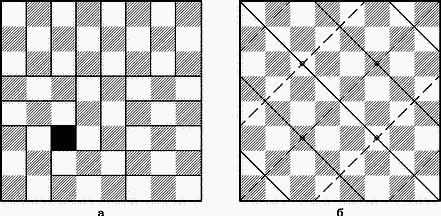
а) б)
Рис. 12
Решение: Одно из покрытий показано на рис. 12,а. Для определения возможных расположений мономино проведем на доске две системы параллельных прямых, как показано на рис. 12,б. Легко убедиться, что при любом покрытии доски каждое тримино покрывает ровно одно поле, через которое проходит сплошная прямая, и ровно одно, через которое проходит пунктирная прямая. Поскольку число полей, пересекаемых сплошными прямыми, равно 22, как и число полей, пересекаемых пунктирными прямыми, а тримино имеется 21, то мономино может занимать лишь поля, пересекаемые обоими семействами прямых. А таких полей всего четыре: c3, c6, f3 и f6. Поворачивая доску на 90°, 180° и 270°, можно получить соответствующее покрытие для каждого из этих четырех полей.
Задачи на раскрашивание и разрезание доски, по-моему, самые легкие математические шахматные задачи. Для решения таких задач единого алгоритма нет, нужны небольшие математические расчеты, хорошее внимание и, конечно, строгие логические рассуждения.
4. Задачи на нахождение числа фигур на шахматной доске,
числа путей передвижения фигур
4.1. Неторопливый король
Король – самая медленная фигура в шахматах. С любого места он может переступать только на соседние поля доски. Однако необычное измерение расстояний на доске лучше всего иллюстрирует движущийся король.
Задача 14. Сколькими способами король с поля е1 может добраться кратчайшим путем до поля d8?
Решение: Очевидно, что кратчайшее путешествие короля до цели занимает семь ходов, причем он может перемещаться любыми зигзагообразными путями, оставаясь при этом внутри прямоугольника e1-a5-d8-h4. Для подсчета искомого числа путей составим таблицу чисел, которые будем помещать прямо на полях доски (рис. 13). Число, стоящее на данном поле равно числу кратчайших путей до него с поля e1. На поля d2, e2 и f2 король может попасть кратчайшим путем единственным способом, и поэтому на них стоят единицы. По той же причине единицы стоят на полях c3 и g3. На d3 за два хода король попадает двумя способами, а на e3 – тремя. В общем случае число кратчайших путей до данного поля складывается из одного, двух или трех чисел, стоящих на полях предыдущей горизонтали, с которых король попадает на данное поле в один ход. Пользуясь этой закономерностью, мы, в конце концов, заполним всю таблицу и получим, что с поля e1 до поля d8 король может добраться кратчайшим путем 357 способами.
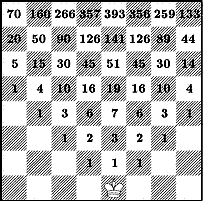
Рис. 13
Задача 15. Какое максимальное число королей можно расставить на доске так, чтобы они не угрожали друг другу, т.е. не стояли рядом?
Решение: Разобьем доску на 16 квадратов (рис. 14). Если мы хотим, чтобы короли не касались друг друга, то, очевидно, в каждом из этих квадратов надо поместить не более одного из них. Это означает, что больше шестнадцати королей, удовлетворяющих условию задачи, расставить невозможно. Итак, максимальное число мирных королей на доске 88 равно 16.

Рис. 14
Задача 16. Какое наименьшее число королей можно расставить на шахматной доске так, чтобы они нападали на все свободные поля доски?
Решение: В каждом из девяти прямоугольников, выделенных на рис. 15, имеется одно поле (на нем стоит король), которое может быть атаковано только королем, находящимся в этом же прямоугольнике. Следовательно, для того чтобы все свободные поля доски были под угрозой, в каждом из наших девяти прямоугольников должен стоять хотя бы один король. Число девять и является решением задачи для обычной доски.

Рис. 15
Задача 17. Двое по очереди передвигают короля, стоящего на доске. Игрок, вынужденный поставить его на поле, которое король уже посетил, проигрывает. На чьей стороне победа?
Решение: Верх берет тот, кто начинает, причем при произвольном положении короля. Для этого он мысленно разбивает доску на прямоугольники 21. Затем первым ходом ставит короля на поле, парное исходному с королем (в том же прямоугольнике). А далее на любой ход соперника передвигает короля на парное ему поле. Таким образом, после каждой пары ходов один прямоугольник «исключается» из игры. В конце концов второму игроку придется занять поле, которое король уже посещал.
4.2. Ферзь на шахматной доске
Ферзь – самая сильная шахматная фигура. Существует множество задач о ферзе. Я думаю, самая распространенная из них – это задача о восьми ферзях.
Задача 18. Сколькими способами можно расставить на шахматной доске восемь ферзей, чтобы они не угрожали друг другу, то есть никакие два не стояли на одной вертикали, горизонтали и диагонали?
Решение: Очевидно, больше восьми ферзей расставить невозможно, тогда хотя бы на одной вертикали и горизонтали их окажется не меньше двух. Найти несколько решений несложно, одно из них показано на рис. 16.
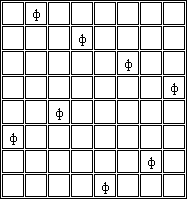
Рис. 16
Многие известные математики пытались решить эту задачу, среди них: М. Беццель, Ф.Наук, В. Аренс. Однако строгое доказательство того, что 92 расстановки исчерпывают все возможности, было получено Д. Глэшером только спустя более 100 лет после открытия этой задачи. Как уже было сказано всего решений 92, но основные из них 12. Остальные получаются при помощи симметрии.
Задача 19. На бесконечной доске находятся два белых ферзя и черный король. За сколько ходов белые могут поставить мат?
Решение: Оказывается, каковы бы ни были размеры доски, и как бы ни располагались в начальный момент два белых ферзя и черный король, мат дается не позднее четвертого хода! Первым ходом один из ферзей объявляет шах по вертикали; в ответ на отступление короля на одну из соседних линий вторым ходом другой ферзь зажимает короля на двух вертикалях. При этом возникает позиция подобная той, что изображена на рис. 17. На любое движение короля на третьем ходу следует соответствующий горизонтальный шах и мат следующим ходом, например 2... Крe4 3. Фc4+ Крe5 (e3) 4. Фf4

Рис.17
4.3. Прямолинейная ладья
Ладья – строгая, прямолинейная фигура. Она тоже часто встречается в математических задачах.
Задача 20. Какое наименьшее число поворотов должна сделать ладья при обходе всех полей доски nn?
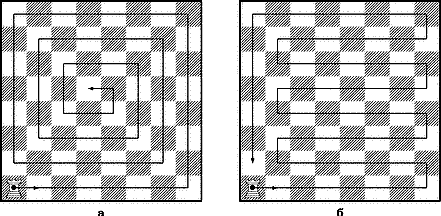
а) б)
Рис. 18
Решение: Ладья должна была сделать хотя бы один ход вдоль каждой вертикали или вдоль каждой горизонтали. Пусть, ладья двигалась хотя бы раз вдоль каждой вертикали. На любую из них, кроме тех, где маршрут начался и закончился, ладья должна была войти и после движения вдоль нее выйти. При этом вход и выход обязательно происходят с поворотами. Таким образом, общее число поворотов не меньше, чем 2(n–2)+1+1=2(n–1). Для любого n маршрут, содержащий ровно столько поворотов, можно получить из маршрута, приведенного на рис. 18,а; при n=8 ладья делает 2(8–1)=14 поворотов. Этот маршрут является открытым, замкнутый маршрут состоит уже из 16 ходов (рис. 18,б).
Задачи на нахождение числа фигур на шахматной доске и числа путей передвижения фигур более сложные, чем задачи на раскрашивание и разрезание доски. Для их решения нужны более сложные расчеты и умение найти математическую закономерность в найденном ряде чисел. Здесь уже большую помощь в решении задачи может оказать умение играть в шахматы.
5. Лабиринты на шахматной доске. Ход конем
Совсем не обязательно быть шахматистом, чтобы знать, какая шахматная фигура самая удивительная. Конечно, это конь! Не случайно выражение «ход конем» стало крылатым и прочно вошло в наш быт. А один из самых остроумных гроссмейстеров, С. Тартаковер, прямо считал, что «вся шахматная партия – это один замаскированный ход конем». Основное свойство коня, которое отличает его от других фигур, состоит в том, что он на каждом своем ходу меняет цвет поля, на котором стоит. Многие задачи о коне удается эффектно решить, если воспользоваться указанным свойством.
Задача 21. Задача о коне Аттилы. На доске находятся две фигуры – белый конь и черный король. Некоторые объявляются «горящими». Конь должен дойти до неприятельского короля, повернуть его и вернуться в исходное положение. Ему запрещено занимать как «горящие» поля, так и поля, уже пройденные им однажды.
«Трава не растёт там, где ступил мой конь!» – похвалялся вождь гуннов Аттила, когда хотел сказать, что его полчища уничтожают всё живое на своём пути. На рис. 19,а конь Аттилы расположен на g4, а неприятельский король – на b3. Горящие поля выделены.
Соединяя отрезками все пары доступных коню полей, между которыми возможен его ход, получаем граф коня для данной задачи (полям доски соответствуют вершины графа) – рис. 19,б. В результате дело сводится к нахождению в графе такого пути, который не содержит ни одной вершины более одного раза и, кроме того, проходит через обе выделенные (на рисунке они обведены кружками).
Методы решения подобных задач, называемых лабиринтами, хорошо известны в теории графов. Впрочем, для коня Аттилы искомый путь нетрудно найти и непосредственно. Он содержит 18 ходов: Кg4-f6-е8-g7-е6-f8-g6-е7-с6-а5:b3-d2-b1-а3-b5-d6-f7-h6-g4. Для достижения цели коню пришлось побывать на 18 полях из 35, не сожжённых в начале сражения.
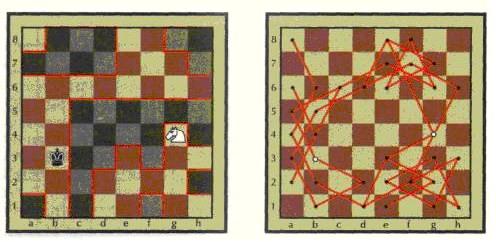
а) б)
Рис. 19
Задача 22. Может ли конь с поля a1 добраться до h8, побывав на каждом поле доски ровно один раз?
Решение: Не может. Исходное поле a1 – черное, и, значит, на каждом нечетном ходу конь попадает на белое поле. Однако число 63 (именно на 63-м ходу конь прибывает в противоположный угол доски) нечетно, а поле h8 – черное.
Все оказалось довольно просто, но любопытно, что за доской шахматист иногда сталкивается с подобными вопросами. Рассмотрим, например, позицию, изображенную на рис.20. Белым здесь удается добиться ничьей единственным путем – 1. Крc1! Теперь их король будет переходить с c1 на c2 и обратно, занимая каждый раз поле того цвета, что и конь, и не выпуская черного короля из заточения. В случае 1. Крc2 конь попадал на d3 при короле на c2, и пешка проходила в ферзи.

Рис. 20
Задача 23. Обойти конем все поля шахматной доски, посетив каждое из них ровно один раз.
Эта задача известна, по крайней мере, с XVIII века. Леонард Эйлер посвятил ей большую работу «Решение одного любопытного вопроса, который, кажется, не подчиняется никакому исследованию» (26 апреля 1757 г.). В письме к Гольдбаху он сообщал: «…Воспоминание о предложенной когда-то мне задаче послужило для меня недавно поводом к некоторым тонким изысканиям, в которых обыкновенный анализ, как кажется, не имеет никакого применения…. Я нашел, наконец, ясный способ находить сколько угодно решений (число их, однако, не бесконечно), не делая проб». Помимо рассмотрения задачи для коня, Эйлер разобрал аналогичные задачи и для других фигур.
Хотя задача была известна и до Эйлера, лишь он впервые обратил внимание на ее математическую сущность, и поэтому задачу часто связывают с его именем.
Метод Эйлера состоит в том, что сначала конь двигается по произвольному маршруту, пока не исчерпает все возможные ходы. Затем оставшиеся непройденными клетки добавляются в сделанный маршрут, после специальной перестановки его элементов.
Фигура коня обозначает начальное положение шахматной фигуры, цифры – его последующие ходы (рис. 21).

Рис. 21. Прохождения коня через все клетки поля шахматной доски 5 × 5.
Известно много методов для нахождения маршрутов коня, которые носят имя первооткрывателей – метод Эйлера и Вандермонда, рамочный метод Мунка и Коллини, метод деления на четверти Полиньяка и Роже и др.
Вот самое простое правило построения маршрутов коня.
Правило Варнсдорфа: при обходе доски коня следует всякий раз ставить на поле, из которого он может сделать наименьшее число ходов на еще не пройденные поля; если таких полей несколько, то можно выбрать любое из них.
Правило Варнсдорфа было предложено более 150 лет назад. Долгое время считалось, что оно действует безукоризненно. Но позднее было установлено, что его вторая часть не совсем точна. Если в распоряжении коня имеется несколько возможностей, упомянутых в первой части правила, то не все они равноценны. Машинный эксперимент показал, что произвольное применение второй части правила Варнсдорфа приводит коня в тупик.
Однако на практике правило Варнсдорфа действует весьма эффективно, и даже при вольном использовании его второй части вероятность заблудиться невелика. Иногда завершить маршрут коня удается даже в том случае, если его начальный путь сделан без всякой системы. На рис. 22,а конь, начав путешествие с поля a1, уже прошел 40 ходов. В этой трудной ситуации, пользуясь правилом Варнсдорфа, конь благополучно заканчивает маршрут. С поля 40 он мог бы пойти, кроме поля f2, на поля c5, d6, f3 и g3. Но каждое из этих полей связано с тремя свободными, а поле f2 – с двумя (hi и d3), этим и объясняется выбор, – число 41 ставится на поле f2. Дальше у коня выбор между полями h1 и d3. Второе поле связано с четырьмя свободными, а первое – только с одним, и число 42 ставится на h1. С этого поля ход определяется однозначно – на поле g3, которое и получает номер 43. Теперь у коня имеется выбор между полями h5 и f5, причем каждое из них связано с тремя свободными. Согласно правилу, можно выбрать любое из них, в нашем случае конь идет на h5 (номер 44). Продвигаясь далее таким же образом, конь в конце концов обойдет всю доску и последним, 63-м ходом, закончит маршрут на поле c6, которое получит номер 64 (см. рис. 22,б).

а) б)
Рис. 22
Неизвестно до сих пор, сколько всего существует маршрутов, Хотя доказано, что число их не более 30 000 000. Многие составители маршрута коня стремились внести в свое занятие, на сколько это возможно, эстетический элемент и достигли любопытных результатов. Придумано множество необычных решений, изображающих различные предметы, буквы или знаки (известен даже график, посвященный Наполеону). Два достопримечательных примера такого рода приведены на рис. 23,а,б. График одного маршрута напоминает собой вазу, а график другого подобен цветку, части которого расположены в высшей степени симметрично.
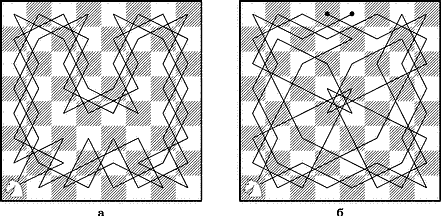
а) б)
Рис. 23
Со времен Эйлера известен так называемый «раздельный ход коня», который заключается в нахождении пути по одной половине доски, его симметричном дублировании и соединении обеих путей вместе (рис. 24). Для половины шахматной доски – доски 8×4 – найдено точное число маршрутов коня. Это позволило подсчитать число «раздельных ходов коня» на доске 8×8, которое и дает нижнюю границу для числа всех решений задачи.
Рис.24
Для того чтобы обойти конём все шахматные клетки и ни разу не побывать дважды на одной и той же, к тому же сделать это «вслепую», начав или закончив на любой клетке по желанию «зрителя», можно благодаря мнемоническому стихотворению:
Алеет Осень Ценными Дарами,
Еще Один Животворящий День.
Хлеба Червонят Желтыми Шнурами,
Хрустальных Вод Философична Сень.
Два Вечера Цеплявшиеся Шишки
Артист Писал, Бездонна Синева.
Дорожный Шлак Целуют Червячишки,
Еще Покрыта Флоксами Трава.
Дымится Чай Эффектней Шоколада,
Фарфоры Чашек Достаются Трем,
Блондинке Девушка Дана Отрада
Форшмак Делить Холодным Острием.
Жена, Толкая Хилую Подругу,
Желает Сняться Этим Выходным,
Ценя Сама Арктическую Вьюгу,
Бросает Шар Арбуза Четверым.
Цикад Пяток, Едва Чревовещая,
Дарует Дрему Фикусам Окна.
Хотя Довольны Жаждавшие Чая,
Хозяин Шумно Жертвует Вина.
Фокстротами Шесть Девушек Пленились,
Эстрадных Танцев Фантастичней Па,
Едва Ступающий Цыпленок Вылез,
А Селезень Блуждающий Пропал.
Алеет Тело Бронзовой Осины,
Царит Теней Ажурная Длина.
Беззвучней, Чем Автомобиля Шины,
Болоту Ветер Дарит Семена.
Фонарь Восьмью Химерами Сияет,
Жук Прилетает, Хлопая, Туда.
Желанна Осень, Если Довершает
Ценнейший Отдых Бодрого Труда.
Первые буквы задают координаты ходов: Алеет Осень = А1; Ценными Дарами = С2; и т. д. В каждую строфу вставлена подсказка, помогающая не перепутать последовательность строф: ещё ОДИН, ДВА вечера, достаются ТРЁМ и т.д.
Значительно труднее проблема, состоящая не в отыскании определенного маршрута коня по доске, а в нахождении всех маршрутов и подсчете их числа. Однако эта задача не решена до сих пор.
6. Задачи о перестановках фигур на шахматной доске
Конечно, одной из самых известных занимательных игр является игра «пятнадцать», придуманная С. Ллойдом. Она относится к перестановочным играм и имеет строгую математическую теорию. И на шахматных досках существует много интересных задач и головоломок, связанных с перестановкой фигур, причем для решения некоторых из них придуман математический приём.
Задача 24 «Пятнадцать». В коробочке 44 находятся пятнадцать квадратов, пронумерованных числами от 1 до 15. Требуется, не вынимая квадраты из коробочки, переставить их так, чтобы номера шли в возрастающем порядке.
Проблема не очень то серьезная, если бы не одно обстоятельство. При попытке уложить фишки в коробочку случайным образом оказывается, что лишь половина из всех возможных комбинаций поддается упорядочению, согласно приведенному условию. Другие комбинации сводятся к расположению, при котором фишки от первой до тринадцатой стоят на своих местах, а две фишки с номерами четырнадцать и пятнадцать поменялись местами. Подобную комбинацию использовал Ллойд для рекламной компании головоломки: за ее решение был назначен приз в несколько тысяч долларов, очень даже приличная сумма по тем временам. Автор ничего не терял, так как «игра в пятнадцать» из данной комбинации была не разрешима. Однако выяснилось это значительно позже, после детального математического описания свойств головоломки.
Всего существует 16! Расположений квадратов, и все они распадаются на два равных по численности класса. Расположения первого класса приводятся при помощи перестановок к нужному расположению квадратов, а расположения второго удается при помощи перестановок привести к нужной позиции, только с переставленными квадратами 14 и 15.
Как определить к какому из двух классов принадлежит данная позиция? Для этого нужно посчитать число транспозиций в ней. Два квадрата образуют транспозицию тогда, когда квадрат с большим номером предшествует квадрату с меньшим. Оказывается, что если число транспозиций чётно, то позиция относится к первому классу, а если нечётно, то ко второму.
Задача 25. На доске 44 расставлены 15 ладей, пронумерованных числами от 1 до 15. Требуется переставить ладьи так, чтобы их номера расположились в возрастающем порядке, а пустым осталось поле d1.
Так как ходы ладьи на доске 44 совпадают с перемещениями квадратов в игре «пятнадцать», эта задача о ладьях изоморфна игре Ллойда. То есть существование ее решения зависит от числа транспозиций ладей в данной позиции (если число транспозиций четно, то решение существует, если нечетно – нет решения).
Задачу о ладьях можно обобщить для досок любого размера. При этом на обычной доске все позиции с 63 пронумерованными ладьями так же распадаются на 2 равных по численности класса: в одном ладьи можно расположить в возрастающем порядке (с пустым полем h1), а в другом – нет. Любопытно, что такая же ситуация имеет место и для коней, т.е. все позиции с 63 пронумерованными конями распадаются на 2 класса, и в половине случаев коней можно расположить в возрастающем порядке, а в половине – нет. Для пронумерованных ферзей и королей необходимая перестановка возможна при любой начальной позиции, а для слонов задача лишена смысла, так как они не могут менять своего цвета.
Задача 26. Старинная головоломка.
Эту задачу придумал итальянец Гуарини ещё в XVI в. Она встречается в книгах по занимательной математике. В углах доски размером 33 стоят два белых и два чёрных коня (рис. 25,а). Требуется поменять местами белых и чёрных коней за наименьшее число ходов.
Наиболее изящно задача решается при помощи «метода пуговиц и нитей», открытого известным мастером математических головоломок Г. Дьюдени. На каждое поле маленькой доски, кроме центрального (на него кони попасть не могут), поместим по пуговице (на рис.25,б их заменяют кружки). Если между двумя полями возможен ход коня, то соответствующие пуговицы свяжем нитью (на рисунке нити – это отрезки прямой). Полученный клубок пуговиц и нитей распутаем так, чтобы все пуговицы расположились по кругу (рис. 25,а).
Теперь задача решается почти автоматически. Выбрав одно из направлений движения по кругу, будем переставлять коней до тех пор, пока они не поменяются местами. Чтобы переместить коней на доске, нужно заменить пуговицы соответствующими полями. Нетрудно убедиться, что решение состоит из 16 перемещений коней (восьми белых и восьми чёрных), причём кони противоположного цвета могут ходить по очереди. Если дополнительно потребовать, чтобы кони разного цвета при движении не угрожали друг другу (очерёдность ходов в этом случае позволяется нарушать), то решение тоже найдём на рис. 25,в. Необходимо только следить за тем, чтобы белые и чёрные кони не оказались соседями в клубке. Если круговое движение (против часовой стрелки) начинает белый конь а1, то решение будет такое: Ка1-b3, Ка3-с2, Кс-b1-а3, Кс1-а2-с3, Кb3-с1-а2, Кс2-а1-b3, Ка3-с2-а1, Кс3-b1-а3, Ка2-с3, Кb3-с1.
а) б) в)
Рис. 25
Метод пуговиц и нитей легко объяснить в терминах теории графов. Действительно, задаче о перестановке коней можно сопоставить граф, вершины которого соответствуют полям доски (пуговицам), а рёбра – возможным ходам коня между полями (нитям). Тогда распутывание клубка пуговиц и нитей есть не что иное, как более наглядное расположение графа на плоскости.
Разумеется, метод пуговиц и нитей может быть использован для решения не только задачи Гуарини, но и целого класса перестановочных задач и головоломок (необязательно шахматных).
17

 Получите свидетельство
Получите свидетельство Вход
Вход











 Математика шахмат (890.5 KB)
Математика шахмат (890.5 KB)
 0
0 2103
2103 118
118 Нравится
0
Нравится
0







