Класс 9
Урок № __61__
Тема: Числовые последовательности
Цели и задачи урока:
Образовательная: Организовать деятельность учащихся по повторению понятий числовой последовательности, арифметической и геометрической прогрессии, содействовать в закреплении навыков словесного, аналитического и рекуррентного задания числовой последовательности, применение полученных знаний на практике.
Развивающая: Содействовать формированию научного мировоззрения, развитию исследовательских навыков, умение подмечать закономерности, аргументировать и классифицировать.
Воспитательная: Содействовать развитию внимательности, умению общаться, инициативности, трудолюбия, творческих способностей, сознательного восприятия учебного материала.
Тип урока: урок обобщающего повторения и систематизации знаний.
Методы обучения: частично – поисковый, системные обобщения
Формы деятельности обучающихся на уроке: фронтальная работа, групповая работа, парная работа, самостоятельная работа, самопроверка, взаимопроверка.
Оборудование: доска, компьютер, мультимедийный проектор, презентация по теме урока, таблички с формулами, магниты
Раздаточный материал: карточки на установление соответствия, карточки с текстом заданий самостоятельной работы, сборники ЕНТ.
ПЛАН УРОКА
| № | Этап урока | Деятельность учителя | Деятельность ученика | Время |
-
| Орг. момент | Приветствие, сообщение темы урока, постановка цели урока. | Формирование задач на урок |
|
-
| Активизация опорных знаний | Проведение математического диктанта в форме разноуровневого теста с взаимопроверкой, оглашение критериев оценивания, раздача оценочных листов | Выполнение задания, взаимопроверка, занесение результатов в оценочные листы |
|
-
| Повторение теоретического материала | Деление на группы, постановка проблемы в рамках одной группы | Решение поставленной проблемы, составление кластера по теме «Числовая последовательность», 1 представитель группы ищет определение понятия «Прогрессия» её историю, составляет кластер. Взаимооценивание |
|
-
| Решение задач | Постановка проблемы. Озвучивание задания упражнения и комментарий задания. | Решение задания. Составление заданий по аналогии. |
|
| Постановка проблемы. Раздача ресурса | Решение задания. Формулирование вопроса. Обсуждение в парах |
|
| Озвучивание вопроса, вызов к обдумыванию и обсуждению | Обдумывание, обсуждение, формирование общей идеи |
|
-
| Рефлексия и постановка Д/з | Раздача листов с вопросами и домашним заданием | Обсуждение вопросов и формирование ответов на них |
|
-
| Итог урока | Выставление оценок с комментарием, | Участие в обсуждении и выставлении оценок |
|
Ход урока:
Организационный этап:
Здравствуйте! Тема нашего урока: «Числовые последовательности».
– Сегодня на уроке мы обобщим и систематизируем те знания, которые получили во время изучения темы «Числовые последовательности».
Эпиграф урока.
Закончился XX век.
Куда стремится человек?
Изучен космос и моря,
Строенье звёзд и вся Земля.
Но математиков зовёт
Известный лозунг:
«Прогрессио – движение вперёд»
(На доске спроецированы цели урока) Ваша задача поставить перед собой Учебные задачи на урок. (Ученики записывают поставленные задачи на стикеры ).
Активизация опорных знаний
Ученикам предлагаются задания, выдаются оценочные листы с критериями оценивания.
| Ф. И. обучающегося | Этапы урока |
| Установи соответствие | Работа в группе по составлению кластера | Решение разноуровневых задач в парах | Решение задач двумя способами. | Обсуждение вопросов в группе |
|
| 7 |
| 5 |
| 5 |
| 3 |
| 5 |
|
| Итог урока | Общее кол-во баллов _____ | Оценка за урок _____ |
Уровень А
Составить определение:
Числовой последовательностью называется множество чисел, элементы которого можно пронумеровать. (1 балл)
Если каждый член последовательности начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом, то эта последовательность называется арифметической прогрессией. (3 балла)
Если каждый член последовательности начиная со второго, равен произведению предыдущего члена на некоторое постоянное число, не равное нулю, то эта последовательность называется геометрической прогрессией. (3 балла)
Уровень В
| № п\п | Вопрос | Формула |
| 1 | Сумма бесконечно убывающей геометрической прогрессии | 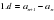
|
| 2 | Формула n-го члена арифметической прогрессии. | 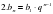
|
| 3 | Сумма n-первых членов арифметической прогрессии. | 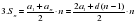
|
| 4 | Сумма n-первых членов геометрической прогрессии. | 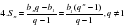
|
| 5 | Формула n-го члена геометрической прогрессии. | 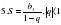
|
| 6 | Знаменатель геометрической прогрессии. | 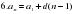
|
| 7 | Разность арифметической прогрессии. | 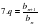
|
| Код ответа:5834291 |
Обучающиеся в течение 5 минут решают предложенные задания, обмениваются тетрадями для взаимопроверки, проводят комментарий допущенных ошибок.
Повторение теоретического материала
Класс делиться на группы. Каждой группе раздается ресурс. Каждой группые необходимо составить кластер на тему «Последовательность. Прогрессия. История возникновения понятий последовательность и прогрессия».
Время работы 7 мин.
Последовательности (ресурс)
Фундаментальную роль числа в природе определил еще Пифагор своим утверждением "Все есть число". Поэтому математика являлась одной из основ религии последователей Пифагора (пифагорейского союза). Пифагорейцы считали, что бог Дионис положил число в основу мировой организации, в основу порядка; оно отражало единство мира, его начало, а мир представлял собой множество, состоящее из противоположностей. То, что приводит противоположности к единству, и есть гармония. Гармония является божественной и заключается в числовых соотношениях.
Слово «прогрессия» латинского происхождения (progressio), буквально означает «движение вперед» ( как и слово «прогресс») и встречается впервые у римского автора Боэция (V-VI вв.).
Прогрессии известны издавна, а потому нельзя сказать, кто их открыл. Ведь и натуральный ряд – это арифметическая прогрессия. Во время раскопок в Египте был найден папирус, который датируется 2000 г. до н.э., но и его было переписано из другого, еще более раннего, отнесенного к ІІІ тысячелетию до н.э. Ученые расшифровали текст папируса, содержание некоторых задач дает возможность отнести их к задачам на прогрессии.
В вавилонских текстах рассказывается о том, что увеличение освещенной части лунного диска на протяжении первых пяти дней происходит по закону геометрической прогрессии со знаменателем 2, а в следующие десять дней – по закону арифметической прогрессии с разностью 16.
Задачи на прогрессии встречаются в одной из древнейших памяток права – «Русской правде», составленной при Киевском князе Ярославе Мудром (ХІ ст.). В этом документе есть статья, посвященная вычислению приплода от 22 овец за 12 лет при условии, что каждая овца ежегодно приносит одну овцу и два барана. Так же содержатся сведения о приплоде от пчел за определенный промежуток времени, о количестве зерна, собранного на определенном участкае земли и др. Эти задачи не имели хозяйственного значения, а были результатом развития интереса к математике и математическому содержанию данных задач.
О том, как давно была известная геометрическая прогрессия, свидетельствует и легенда об истории изобретения шахмат. Изобретатель шахмат, ученый Сета, попросил в награду у индийского царя Сирама за свое изобретение столько пшеничных зерен, сколько их получится, если на первую клеточку шахматной доски положить одно зерно, на вторую – два, на третью- четыре, т.е. чтобы число зерен все время удваивалось. Рассказывают, что индийский царь Сирам рассмеялся, услышав, какую награду попросил у него изобретатель шахмат.
Сколько зёрен должен был получить изобретатель шахмат? (Учащиеся должны подсчитать дома)
S64 = 264 – 1 = 18 446 744 073 709 551 615.
Современники сказали бы так:
S64 = 1, 84• 1019 – стандартный вид данного числа.
Если бы царю удалось засеять пшеницей площадь всей поверхности Земли, считая и моря , и океаны, и пустыни, и Арктику с Антарктикой, то получить удовлетворительный урожай, то за пять лет он смог бы рассчитаться с просителем. Такое количество зерен пшеницы можно собрать лишь с площади в 2000 раз большей поверхности Земли. Это превосходит количество пшеницы, собранной человечеством до нашего времени.
Чтобы разместить это зерно в амбаре, то его размеры будут: высота 4 м, ширина 10м, длина будет 30 000 000км- вдвое больше, чем расстояние от Земли до Солнца
Решение задач
- В группах решить задачи, обсудить решение внутри группы.
1. Дана арифметическая прогрессия: -8, -16, … Найдите разность арифметической прогрессии.
2. Найдите знаменатель геометрической прогрессии, если 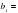 12,
12, 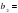 4.
4.
--------------------------------------------------------------------------------------------
3. Найдите пятый член геометрической прогрессии 4, 1, …
4. Найти седьмой член арифметической прогрессии, если 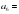 15,
15, 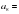 - 4.
- 4.
----------------------------------------------------------------------------------------------
- В розданных сборниках ЕНТ найти задания на прогрессию, числовую последовательность и решить с обсуждением в парах.
- подумайте, что дает нам знание формул n-го члена арифметической и геометрической прогрессии
Составить задачи по аналогии с дальнейшим взаимообменом для решения.
Взаимооценивание.
Физ.минутка
Задача из папируса Райнда звучит так:
«У семи лиц по семи кошек; каждая кошка съедает по семи мышей, каждая мышь съедает по семи колосьев, из каждого колоса может вырасти по семь мер ячменя. Как велики числа этого ряда и их сумма?»
Решение задачи выполняется в тетрадях и на доске.
Людей всего 7, кошек 72=49, они съедают 73=343 мыши, которые съедают всего 74=2401 колосьев, из них вырастает 75=16807 мер ячменя. В сумме эти числа дают 19 607.
Парам предлагается решить задачи двумя способами:
1) Не используя формул прогрессий;
2) Используя изученные формулы арифметической и геометрической прогрессии.
Задача первой группе (решают самостоятельно)
Как известно из медицинской статистики, одна выкуренная сигарета сокращает жизнь человека на 10 минут. Вычислите, сколько сигарет в среднем сократят жизнь человека на 1 день. (144 сигареты).
Задача второй группе (решают самостоятельно)
Курс воздушных ванн начинает с 15 минут в первый день и увеличивают время этой процедуры в каждый следующий день на 10 мин. Сколько дней следует принимать воздушные ванны в указанном режиме, чтобы достичь их максимальной продолжительности 1ч 45 мин? Ответ: 10 дней
Рефлексия. Постановка Д/з.
Ответить на поставленные вопросы:
Из области, каких наук данные задачи?
Какой способ позволяет быстрее решить задачи?
Что было бы, если бы вы не знали формул прогрессий?
Для чего необходимо изучать арифметическую и геометрическую прогрессии?
Приведите ещё примеры наук или специальностей, которые могут использовать знания по арифметической и геометрической прогрессии.
Д/з :
А)Задача
В благоприятных условиях бактерии размножаются так, что на протяжении одной минуты одна из них делится на две. Указать количество бактерий, рожденных одной бактерией за 7 минут.
Б) Придумать и составить задачу на применение знаний по прогрессии в вашей будущей специальности.
Прошу вас взять ваши стикеры и сделать анализ, достигли ли вы поставленных перед собой задач?
А теперь выберите смайлик, характеризующий ваше настроение на конец урока и поставьте его на той ступеньке лестницы-успеха, которой вы достигли к концу урока по вашему мнению.



Обсуждение и выставление оценок.
Урок сегодня завершён,
Но каждый должен знать:
Познание, упорство, труд
К прогрессу в жизни приведут.
| Ф. И. обучающегося | Этапы урока |
| Установи соответствие | Работа в группе по составлению кластера | Решение разноуровневых задач в парах | Решение задач двумя способами. | Обсуждение вопросов в группе |
|
| 7 |
| 5 |
| 5 |
| 3 |
| 5 |
|
| Итог урока | Общее кол-во баллов _____ | Оценка за урок _____ |
| Ф. И. обучающегося | Этапы урока |
| Установи соответствие | Работа в группе по составлению кластера | Решение разноуровневых задач в парах | Решение задач двумя способами. | Обсуждение вопросов в группе |
|
| 7 |
| 5 |
| 5 |
| 3 |
| 5 |
|
| Итог урока | Общее кол-во баллов _____ | Оценка за урок _____ |
| Ф. И. обучающегося | Этапы урока |
| Установи соответствие | Работа в группе по составлению кластера | Решение разноуровневых задач в парах | Решение задач двумя способами. | Обсуждение вопросов в группе |
|
| 7 |
| 5 |
| 5 |
| 3 |
| 5 |
|
| Итог урока | Общее кол-во баллов _____ | Оценка за урок _____ |
| Ф. И. обучающегося | Этапы урока |
| Установи соответствие | Работа в группе по составлению кластера | Решение разноуровневых задач в парах | Решение задач двумя способами. | Обсуждение вопросов в группе |
|
| 7 |
| 5 |
| 5 |
| 3 |
| 5 |
|
| Итог урока | Общее кол-во баллов _____ | Оценка за урок _____ |
| Ф. И. обучающегося | Этапы урока |
| Установи соответствие | Работа в группе по составлению кластера | Решение разноуровневых задач в парах | Решение задач двумя способами. | Обсуждение вопросов в группе |
|
| 7 |
| 5 |
| 5 |
| 3 |
| 5 |
|
| Итог урока | Общее кол-во баллов _____ | Оценка за урок _____ |
Задача первой группе (решают самостоятельно)
Как известно из медицинской статистики, одна выкуренная сигарета сокращает жизнь человека на 10 минут. Вычислите, сколько сигарет в среднем сократят жизнь человека на 1 день.
Задача первой группе (решают самостоятельно)
Как известно из медицинской статистики, одна выкуренная сигарета сокращает жизнь человека на 10 минут. Вычислите, сколько сигарет в среднем сократят жизнь человека на 1 день.
Задача второй группе (решают самостоятельно)
Курс воздушных ванн начинает с 15 минут в первый день и увеличивают время этой процедуры в каждый следующий день на 10 мин. Сколько дней следует принимать воздушные ванны в указанном режиме, чтобы достичь их максимальной продолжительности 1ч 45 мин?
Задача второй группе (решают самостоятельно)
Курс воздушных ванн начинает с 15 минут в первый день и увеличивают время этой процедуры в каждый следующий день на 10 мин. Сколько дней следует принимать воздушные ванны в указанном режиме, чтобы достичь их максимальной продолжительности 1ч 45 мин?
Вопросы для обсуждения:
Из области, каких наук данные задачи?
Какой способ позволяет быстрее решить задачи?
Что было бы, если бы вы не знали формул прогрессий?
Для чего необходимо изучать арифметическую и геометрическую прогрессии?
Приведите ещё примеры наук или специальностей, которые могут использовать знания по арифметической и геометрической прогрессии.
Вопросы для обсуждения:
Из области, каких наук данные задачи?
Какой способ позволяет быстрее решить задачи?
Что было бы, если бы вы не знали формул прогрессий?
Для чего необходимо изучать арифметическую и геометрическую прогрессии?
Приведите ещё примеры наук или специальностей, которые могут использовать знания по арифметической и геометрической прогрессии.
1. Дана арифметическая прогрессия: -8, -16, … Найдите разность арифметической прогрессии.
2. Найдите знаменатель геометрической прогрессии, если 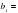 12,
12, 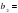 4.
4.
--------------------------------------------------------------------------------------------
3. Найдите пятый член геометрической прогрессии 4, 1, …
4. Найти седьмой член арифметической прогрессии, если 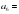 15,
15, 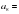 - 4.
- 4.
----------------------------------------------------------------------------------------------
1. Дана арифметическая прогрессия: -8, -16, … Найдите разность арифметической прогрессии.
2. Найдите знаменатель геометрической прогрессии, если 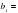 12,
12, 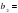 4.
4.
--------------------------------------------------------------------------------------------
3. Найдите пятый член геометрической прогрессии 4, 1, …
4. Найти седьмой член арифметической прогрессии, если 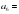 15,
15, 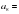 - 4.
- 4.
----------------------------------------------------------------------------------------------
1. Дана арифметическая прогрессия: -8, -16, … Найдите разность арифметической прогрессии.
2. Найдите знаменатель геометрической прогрессии, если 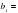 12,
12, 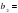 4.
4.
--------------------------------------------------------------------------------------------
3. Найдите пятый член геометрической прогрессии 4, 1, …
4. Найти седьмой член арифметической прогрессии, если 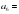 15,
15, 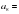 - 4.
- 4.
----------------------------------------------------------------------------------------------
1. Дана арифметическая прогрессия: -8, -16, … Найдите разность арифметической прогрессии.
2. Найдите знаменатель геометрической прогрессии, если 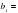 12,
12, 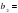 4.
4.
--------------------------------------------------------------------------------------------
3. Найдите пятый член геометрической прогрессии 4, 1, …
4. Найти седьмой член арифметической прогрессии, если 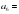 15,
15, 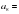 - 4.
- 4.
----------------------------------------------------------------------------------------------
1. Дана арифметическая прогрессия: -8, -16, … Найдите разность арифметической прогрессии.
2. Найдите знаменатель геометрической прогрессии, если 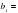 12,
12, 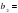 4.
4.
--------------------------------------------------------------------------------------------
3. Найдите пятый член геометрической прогрессии 4, 1, …
4. Найти седьмой член арифметической прогрессии, если 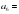 15,
15, 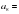 - 4.
- 4.
----------------------------------------------------------------------------------------------
Последовательности (ресурс)
Фундаментальную роль числа в природе определил еще Пифагор своим утверждением "Все есть число". Поэтому математика являлась одной из основ религии последователей Пифагора (пифагорейского союза). Пифагорейцы считали, что бог Дионис положил число в основу мировой организации, в основу порядка; оно отражало единство мира, его начало, а мир представлял собой множество, состоящее из противоположностей. То, что приводит противоположности к единству, и есть гармония. Гармония является божественной и заключается в числовых соотношениях.
Слово «прогрессия» латинского происхождения (progressio), буквально означает «движение вперед» ( как и слово «прогресс») и встречается впервые у римского автора Боэция (V-VI вв.).
Прогрессии известны издавна, а потому нельзя сказать, кто их открыл. Ведь и натуральный ряд – это арифметическая прогрессия. Во время раскопок в Египте был найден папирус, который датируется 2000 г. до н.э., но и его было переписано из другого, еще более раннего, отнесенного к ІІІ тысячелетию до н.э. Ученые расшифровали текст папируса, содержание некоторых задач дает возможность отнести их к задачам на прогрессии.
В вавилонских текстах рассказывается о том, что увеличение освещенной части лунного диска на протяжении первых пяти дней происходит по закону геометрической прогрессии со знаменателем 2, а в следующие десять дней – по закону арифметической прогрессии с разностью 16.
Задачи на прогрессии встречаются в одной из древнейших памяток права – «Русской правде», составленной при Киевском князе Ярославе Мудром (ХІ ст.). В этом документе есть статья, посвященная вычислению приплода от 22 овец за 12 лет при условии, что каждая овца ежегодно приносит одну овцу и два барана. Так же содержатся сведения о приплоде от пчел за определенный промежуток времени, о количестве зерна, собранного на определенном участкае земли и др. Эти задачи не имели хозяйственного значения, а были результатом развития интереса к математике и математическому содержанию данных задач.
О том, как давно была известная геометрическая прогрессия, свидетельствует и легенда об истории изобретения шахмат. Изобретатель шахмат, ученый Сета, попросил в награду у индийского царя Сирама за свое изобретение столько пшеничных зерен, сколько их получится, если на первую клеточку шахматной доски положить одно зерно, на вторую – два, на третью- четыре, т.е. чтобы число зерен все время удваивалось. Рассказывают, что индийский царь Сирам рассмеялся, услышав, какую награду попросил у него изобретатель шахмат.
Сколько зёрен должен был получить изобретатель шахмат? (Учащиеся должны подсчитать дома)
S64 = 264 – 1 = 18 446 744 073 709 551 615.
Современники сказали бы так:
S64 = 1, 84• 1019 – стандартный вид данного числа.
Если бы царю удалось засеять пшеницей площадь всей поверхности Земли, считая и моря , и океаны, и пустыни, и Арктику с Антарктикой, то получить удовлетворительный урожай, то за пять лет он смог бы рассчитаться с просителем. Такое количество зерен пшеницы можно собрать лишь с площади в 2000 раз большей поверхности Земли. Это превосходит количество пшеницы, собранной человечеством до нашего времени.
Чтобы разместить это зерно в амбаре, то его размеры будут: высота 4 м, ширина 10м, длина будет 30 000 000км- вдвое больше, чем расстояние от Земли до Солнца
Установи соответствие:
| № п\п | Вопрос | Формула |
| 1 | Сумма бесконечно убывающей геометрической прогрессии | 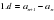
|
| 2 | Формула n-го члена арифметической прогрессии. | 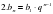
|
| 3 | Сумма n-первых членов арифметической прогрессии. | 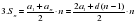
|
| 4 | Сумма n-первых членов геометрической прогрессии. | 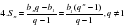
|
| 5 | Формула n-го члена геометрической прогрессии. | 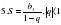
|
| 6 | Знаменатель геометрической прогрессии. | 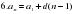
|
| 7 | Разность арифметической прогрессии. | 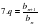
|
| Код ответа: |
Установи соответствие:
| № п\п | Вопрос | Формула |
| 1 | Сумма бесконечно убывающей геометрической прогрессии | 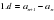
|
| 2 | Формула n-го члена арифметической прогрессии. | 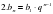
|
| 3 | Сумма n-первых членов арифметической прогрессии. | 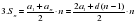
|
| 4 | Сумма n-первых членов геометрической прогрессии. | 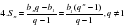
|
| 5 | Формула n-го члена геометрической прогрессии. | 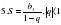
|
| 6 | Знаменатель геометрической прогрессии. | 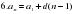
|
| 7 | Разность арифметической прогрессии. | 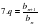
|
| Код ответа: |
Числовой последовательностью называется множество чисел, элементы которого можно пронумеровать.
Если каждый член последовательности начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом, то эта последовательность называется арифметической прогрессией.
Если каждый член последовательности начиная со второго, равен произведению предыдущего члена на некоторое постоянное число, не равное нулю, то эта последовательность называется геометрической прогрессией.

 Получите свидетельство
Получите свидетельство Вход
Вход


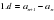
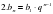
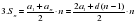
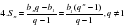
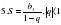
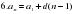
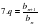
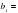 12,
12, 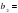 4.
4.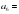 15,
15, 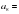 - 4.
- 4.











 Числовые последовательности (79.68 КB)
Числовые последовательности (79.68 КB)
 0
0 2411
2411 299
299 Нравится
0
Нравится
0


