Материал по математике по теме "Фонд оценочных средств по дисциплине Математика"

ВОПРОСЫ К ЭКЗАМЕНУ по дисциплине «Математика» специальность 23. 02. 03 «Техническое обслуживание и ремонт автомобильного транспорта», 1 курс, 1 семестр

1. Абсолютная и относительная погрешность. Запись приближенных чисел.

2. Рациональные числа. Иррациональные числа. Понятие о мнимых и комплексных числах.

3. Геометрическая интерпретация комплексных чисел. Модуль комплексного числа.

4. Арифметические действия над комплексными числами, заданными в алгебраической форме.

5. Понятие функции. Основные свойства функции.

6. Степень с произвольным показателем, ее свойства.

7. Степенная функция, ее свойства и график.

8. Показательная функция, ее свойства и график.

9. Логарифмическая функция, ее свойства и график.

10. Логарифмы и их свойства. Натуральные и десятичные логарифмы.

11. Иррациональные уравнения. Методы решения.

12. Корень n-степени, его свойства.

13. Показательные уравнения и неравенства. Методы решения.

14. Логарифмические уравнения и неравенства. Методы их решения.

15. Тригонометрические функции числового аргумента. Знаки их значений.

16. Тригонометрические функции y = cosx, y = sinx, их свойства и графики.

17. Тригонометрические функции y = tgx, y = ctgx, их свойства и графики.

18. Основные тригонометрические тождества. Выражение тригонометрических функций через другие.

19. Преобразование графиков тригонометрических функций.

20. Обратные тригонометрические функции. Arccosa, arcsina, определение и свойства.

21. Обратные тригонометрические функции. Arctga, arcctga, определение и свойства.

22. Простейшее тригонометрическое уравнение cosx = a. Формула корней. Особая форма записи корней уравнений cosx = 0, cosx = 1, cosx = -1.

23. Простейшее тригонометрическое уравнение sinx = a. Формула корней. Особая форма записи корней уравнений sinx = 0, sinx = 1, sinx = -1.

24. Простейшие тригонометрические уравнения tgx = a, ctgx = a. Формулы корней.

25. Решение тригонометрических уравнений методом подстановки.

26. Простейшие тригонометрические неравенства, алгоритм решения.

27. Радианное измерение дуг и углов. Формулы перехода от градусного измерения к радианному и наоборот.

28. Предел функции. Бесконечно малые и бесконечно большие величины.

29. Понятие производной функции. Правила вычисления производных. Основные формулы дифференцирования.

30. Геометрический смысл производной. Признаки возрастания и убывания функции.

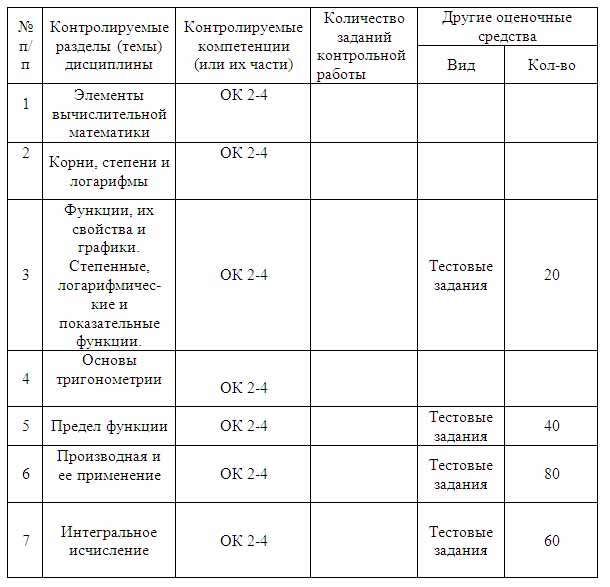
Паспорт. Фонда оценочных средств по дисциплине «Математика»

ВОПРОСЫ К ЭКЗАМЕНУспо дисциплине «Математика»сспециальность 23. 02. 03 «Техническое обслуживание и ремонт автомобильного транспорта», 1 курс, 2 семестр

1. Алгоритм исследования функции на максимум и минимум. Нахождение наименьшего и наибольшего значения функции.

2. Схема исследования функций.

3. Первообразная. Неопределенный интеграл и его свойства.

4. Таблица основных неопределенных интегралов. Интегрирование методом подстановки.

5. Определенный интеграл и его геометрический смысл. Формула Ньютона-Лейбница.

6. Применение определенного интеграла. Для вычисления площадей плоских фигур.

7. Основные понятия и аксиомы стереометрии, следствия из аксиом.

8. Следствия из аксиом стереометрии. Доказательство одного из них.

9. Взаимное расположение двух плоскостей. Признак параллельности двух плоскостей (доказательство).

10. Взаимное расположение прямых в пространстве. Признак параллельности прямых.

11. Взаимное расположение прямой и плоскости. Признак параллельности прямой и плоскости (доказательство).

12. Перпендикулярность прямой и плоскости. Признак перпендикулярности прямой и плоскости.

13. Перпендикуляр и наклонная. Угол между прямой и плоскостью. Теорема о трех перпендикулярах.

14. Двугранные и многогранные углы. Перпендикулярность двух плоскостей.

15. Векторы на плоскости и в пространстве. Действия над векторами.

16. Уравнение прямой на плоскости. Способы задания.

17. Понятие о многограннике. Призма. Площадь ее поверхности.

18. Параллелепипед, его свойства. Площадь его поверхности. Теорема о диагоналях прямоугольного параллелепипеда.

19. Пирамида. Площадь ее поверхности.

20. Правильные многогранники.

21. Цилиндр. Площадь его поверхности.

22. Конус. Площадь его поверхности.

23. Шар и сфера. Площадь поверхности сферы.

24. Понятие объема тела. Объем призмы, параллелепипеда, пирамиды.

25. Понятие объема тела. Объем цилиндра, конуса, шара.

26. Элементы комбинаторики.

27. Элементы теории вероятностей.

28. Основные задачи и понятия математической статистики.

29. Применение производной для применения приближенных вычислений.

30. Статистическое распределение выборки.

Полную информацию смотрите в файле.