Квадратичная функция

Квадратичная

функция

План урока

• Определение квадратичной функции

• Свойства квадратичной функции

• График квадратичной функции
• Преобразование графиков функции

Растяжение или сжатие графика y=ax 2

• Растяжение или сжатие графика y=ax 2

• Паралельнон перенесение графика вида y=a(x — m) 2 Паралельное перенесение графика вида y=a(x - m) 2 +n
• Паралельнон перенесение графика вида y=a(x — m) 2
• Паралельное перенесение графика вида y=a(x - m) 2 +n

Определение квадратичной

функции

Функцией называют такую зависимость переменной У от переменной х, при которой каждому значению переменной х соответствует одно единственное значение переменной у.

Квадратичной функцией называют функцию вида:

y = ax2 + bx + c ,

гдг x – независимая переменная,

a , b и c – некоторые числа, причем a≠ 0 .

Усно: 1. Среди следующих функций найдите квадратичные: а) у=-х+25 б) в) г) д) е) є) 2. Дано функцию f( х)= . Найдите: а) f( 0), б) f( 1), f( -1)

Письменно: №159(а,в) №160 (а,в) №161 №162(а)

0,Da0,D0 a0,D=0 x 1 x 1 x x 2 x x y y y aa0 ax x x 1 x x 1 x 2 " width="640"

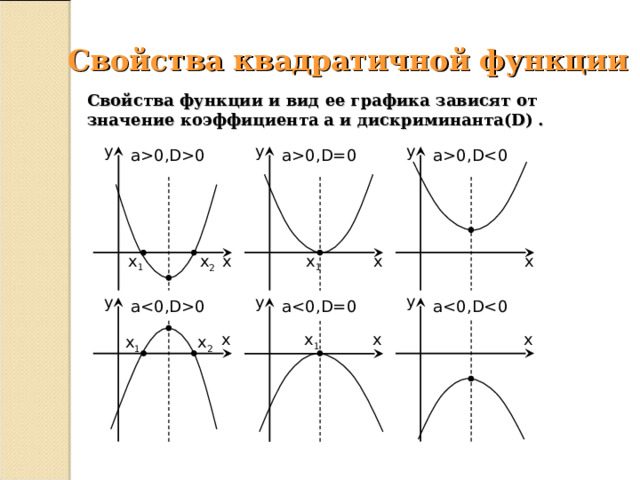
Свойства квадратичной функции

Свойства функции и вид ее графика зависят от

значение коэффициента a и дискриминанта(D) .

y

y

y

a0,D

a0,D0

a0,D=0

x 1

x 1

x

x 2

x

x

y

y

y

a

a0

a

x

x

x 1

x

x 1

x 2

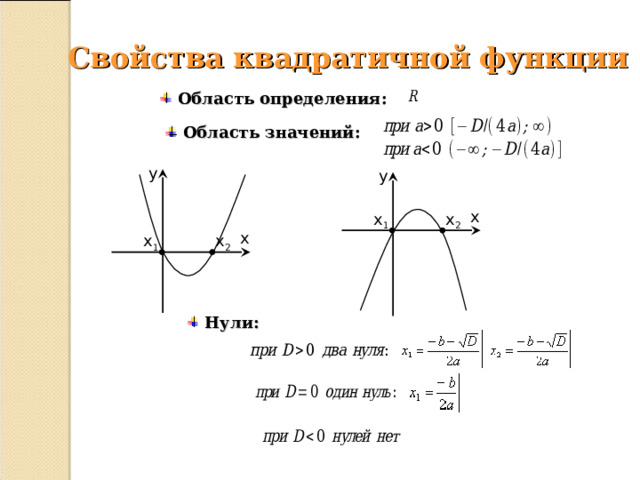
Свойства квадратичной функции

• Область определения:

• Область значений:

y

y

x

x 1

x 2

x

x 1

x 2

• Нули:

График квадратичной функции

Графиком квадратичной функции является парабола-кривая, симметричная относительно прямой x= - b / (2а), которая проходит через вершину параболы (вершиной параболы называют точку пересечения параболы с осью симметрии).

Чтобы построить график квадратичной функции,

вам необходимо:

• Найти координаты вершины параболы и пометить ее на

координатной плоскости

2) Построить несколько точек, принадлежащих параболе-точки пересечения с осями ОХ и ОУ;

3) соединить все точки плавной линией.

y=x 2

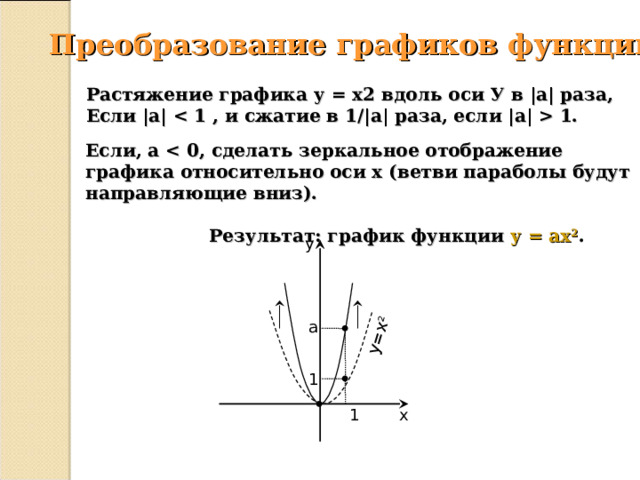
Преобразование графиков функции

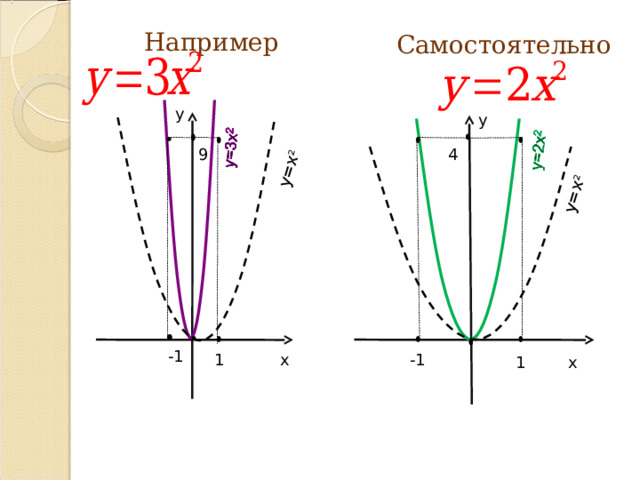
Растяжение графика у = х2 вдоль оси У в |а| раза, Если |а| 1.

Если, а

Результат: график функции у = ах 2 .

y

a

1

x

1

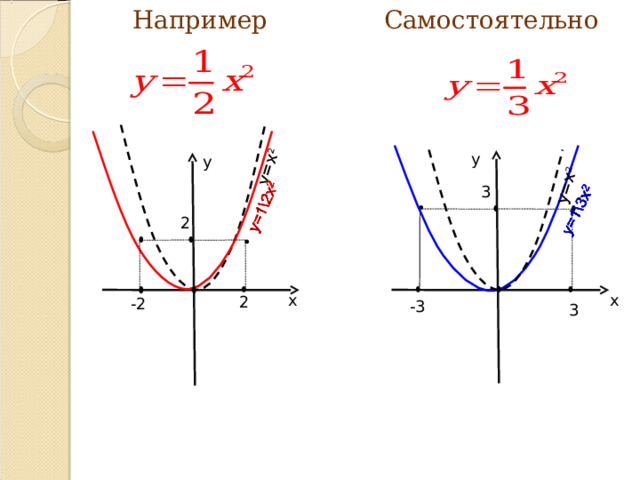
Например

Самостоятельно

y=x 2

y=x 2

у

у

3

2

х

х

2

-2

-3

3

y=x 2

y=x 2

Например

Самостоятельно

у

у

4

9

-1

1

х

-1

х

1

0 и слева, если m Результат: график функции у = а(х - m) 2 . y x m " width="640"

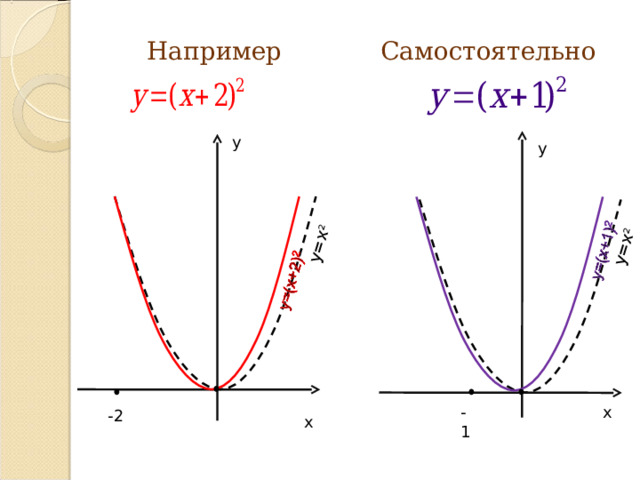
y = a(x – m) 2

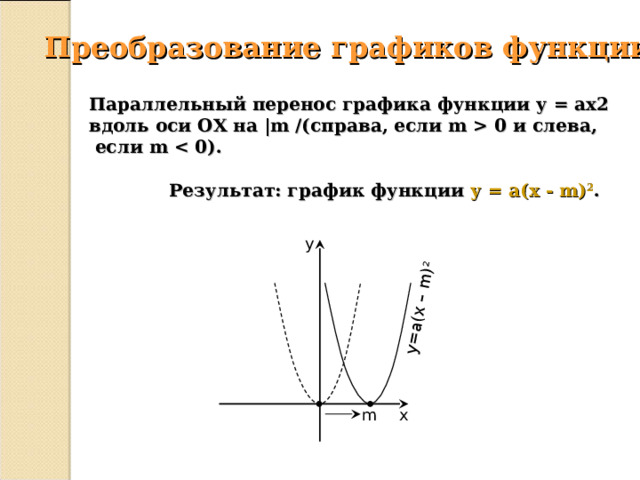
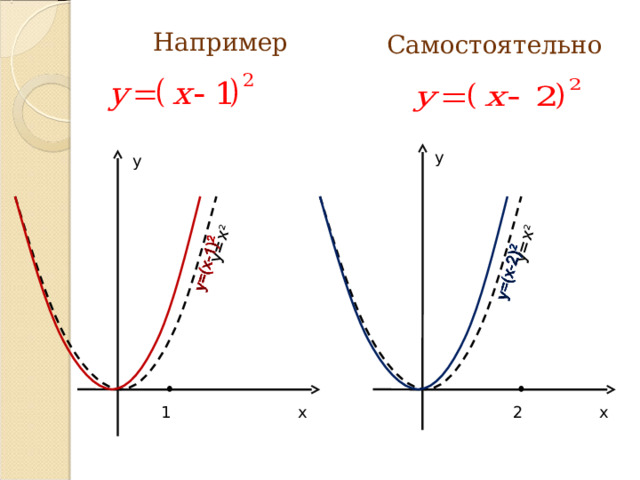
Преобразование графиков функции

Параллельный перенос графика функции у = ах2 вдоль оси ОХ на |m /(справа, если m 0 и слева,

если m

Результат: график функции у = а(х - m) 2 .

y

x

m

y=x 2

y=x 2

Например

Самостоятельно

у

у

1

х

х

2

y=x 2

y=x 2

Например

Самостоятельно

у

у

-1

х

-2

х

0 и вниз при n Результат: график функции у = ах 2 + n . y n x 15 " width="640"

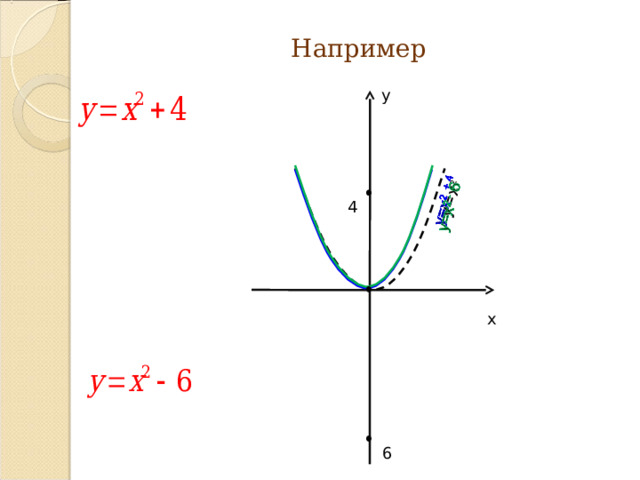
y=ax 2 +n

Преобразование графиков функции

Параллельный перенос графика функции

y = ax 2 вдоль оси ОУ в |n| (вверх при n 0 и вниз при n

Результат: график функции у = ах 2 + n .

y

n

x

15

y=x 2

Например

у

4

х

6

0 и вниз при n Результат: график функции у = а(х - m) 2 + n . y n x m " width="640"

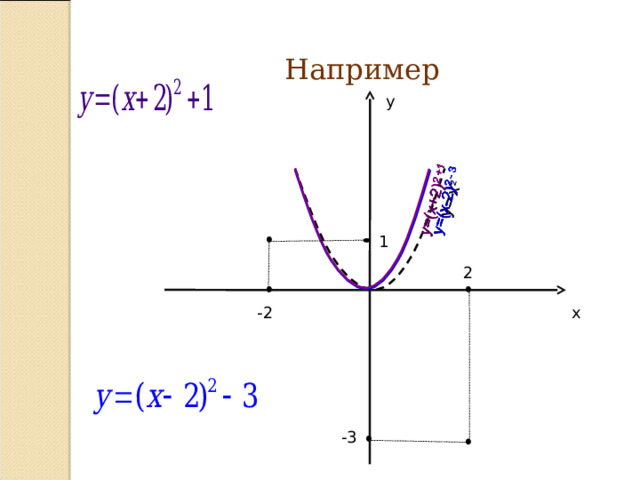
y=a(x – m) 2 +n

Преобразование графиков функции

Параллельный перенос графика функции

y = a (x - m)2 вдоль оси ОУ в |n| (вверх при n 0 и вниз при n

Результат: график функции у = а(х - m) 2 + n .

y

n

x

m

y=x 2

Например

у

1

2

х

-2

-3

18

Домашнее задание :

п.10 стр.85

Виполнить

№ 10.10,

10.18,

10.20