2+n и y=a(x-m)² и их графики"">Презентация по математике "Квадратичная функция. Функции вида y=ax²+n и y=a(x-m)² и их графики"

Цели урока:

Способствовать:

а) формированию знаний основных понятий, входящих в тему;

б) выработке умений работать самостоятельно с теоретическим материалом на уровне анализа и вычленения главного;

в) умению строить графики функций вида y=ax² + n и y=a(x-m) ^2.

Задачи урока:

Образовательные:

- формировать навыки построения графиков функций в ходе урока и самостоятельной работе;

- развивать умение и навыки учащихся работать самостоятельно с теоретическим и практическим материалом на уровне анализа вычленения главного.

Развивающие:

- развивать критическое мышление;

- развивать познавательную активность.

Воспитательные:

- содействовать расширению кругозора;

- развивать самостоятельность и творчество, чувство отвественности, толерантности.

Тип урока: изучение нового материала.

Место урока: первый из четырех уроков по данной теме.

Методы: проблемно поисковый, наглядные, дедуктивные, продуктивные, практические.

Используемые средства обучения: карточки-заготовки для построения графика функций, шаблоны, парабол y=x² y=2x² ; y= x² карточки с заданиями, источник Интернет ресурса.

Сопровождение к уроку: экран, проектор, компьютерная презентация, учебник Алгебра-8, автор А. Е. Абылкасымова (Мектеп, 2012)

Структура урока.

1. Организационный этап.

2. Постовка проблемы.

3. Актуализация знаний.

4. Исследование.

5. Проверочная работа с взаимопроверкой.

6. Проведение итогов урока.

7. Домашние задание.

8. Рефлексия.

Ход урока.

1. Организационный момент.

Приветствие учащихся, проверка их готовности к уроку.

2. Сообщение темы урока.

3. Постановка проблемы.

График квадратичной функции вокруг нас

(компьютерные презентации).

4. Актуализация знаний.

Из курса алгебры 7 класса вам знакома функция у=ах²

- что это за функция?

- что служит графиком этой функции?

- чем отличаются графики функций y=x² и y=-x² ; y=x² и y=x² ; y=x² и y=2x^2.

- сделайте вывод: на что указывает знак коэффициента “а”, значение коэффициента “а”.

Функция у=ах² является частным случаем функции y=aх²+bx+c.

На странице 85 учебника найдите ответ на вопрос как называется функция, заданная формулой y=ax² + bx+ c.

Таким образом, графиком квадратичной функции является парабола. Параболу можно встретить и в окружающем нас мире (компьютерная презентация) .

5. Исследование:

Итак, что же вы знаете пока о квадратичной функции?

Фронтальный опрос

Вместо многоточия поставить пропущенные слова

(на экране)

1. Функция вида y= ax² + bx + c, где a, b, c-. . . , причем. . . 0, x-. . . , называется. . . функцией.

2. Функция y=x² – это функция y=ax² +. . . +. . . , при а=. . . , b=. . . , c=. . . .

3. Кривая, являющаяся графиком функции у=х² называется. . . .

4. Парабола у=х² касается оси ОХ в точке с координатами (. . . ).

5. График функции у=х² симметричен относительно оси. . . .

6. Ось ОУ является осью. . . параболы.

7. При а. . . 0 ветви параболы у=ах² направлены вверх, а при а. . . 0-вниз.

А теперь рассмотрим функции у=ах² + n и у=а(х-m) ^2, а именно у=х² + 2 и у=(х-3) ^2.

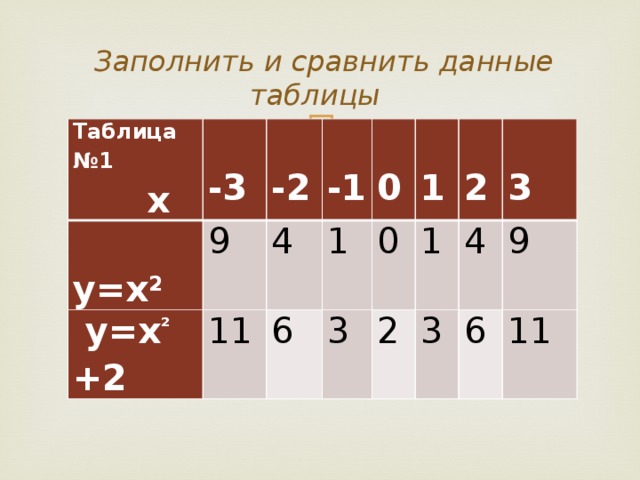
 Заполнить и сравнить данные таблицы 1 (у каждого ученика на столе по 2 таблицы).

Таблица 1

Учащиеся самостоятельно заполняют таблицу, а затем проверяют по экрану

Вывод: при одних и тех же значениях х значения функции у=х² +2 на 2 единицы больше, чем значения функции у=х^2. Таким образом, график функции

у=х² + 2 можно получить из графика функции у=х² путем движения по оси ОY на 2 единицы вверх.

Постройте в одной координатной плоскости графики этих функций, используя шаблон параболы у=х² (разными цветами).

Выпишите координаты вершины параболы для каждой из построенных функций.

1) (0;0) 2) (0;2)

А теперь в этой же координатной плоскости с помощью того же шаблона постройте график функций у=х² – 2.

Сделайте вывод:

Как построить график функции у=ах² + n при n>0, при n<0, применяя функцию y=ax² ?

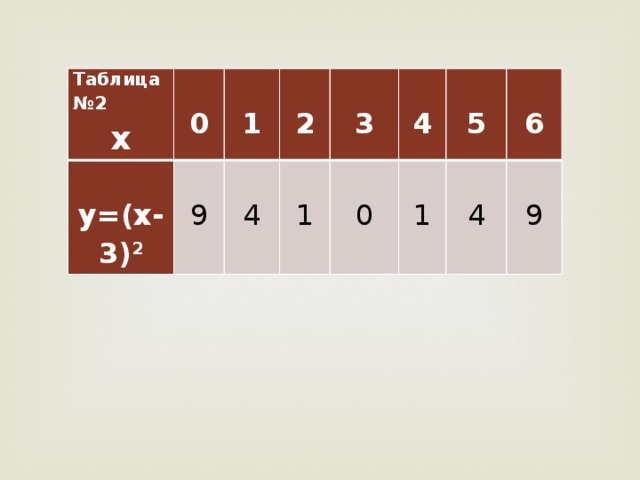
Далее, заполните таблицу 2

Отметьте на координатной плоскости точки, координаты которых указаны в таблице, соединив их плавной линией, получим график функции у=(х-3) ².

В этой же плоскости постройте график функции у=х² (с помощью шаблона)

Сделайте вывод, график функции у=а(х-m) ² есть парабола, полученная из графика функции у=ах² в результате сдвига вправо вдоль оси абсцисс на m единиц при m>0 или влево на ImI единиц при m<0.

Координаты вершины параболы (m; 0)

А как вы думаете, что представляет из себя график функции у=а(х-m) ² +n ?

И как можно построить график этой функции, используя сегодняшние знания?

Об этой функции и свойствах квадратичной функции будем говорить на следующем уроке, а сейчас вашему вниманию примеры зависимостей, выраженных через квадратичную функцию. Подготовленные заранее учащиеся делают краткие сообщения.

Примерами зависимости, выраженных через квадратичную функцию является:

1. Уравнение координаты тела, действующего под действием постоянной силы: Х=Х₀ +V₀t + a , здесь t – переменная.

2. А еще: зависимость кинетической энергии от скорости W =.

3. А еще примерами зависимости, выраженных через квадратичную функцию является:

Орбита, по которой тело будет двигаться вокруг Земли со второй космической скоростью, равной 11, 18 м/c, будет параболической.

4. А еще, тела, брошенные горизонтально или под углом к горизонту будут двигаться по параболической траектории под действие силы тяжести.

А теперь пришло время показать, чему вы научились сегодня на уроке.

6. Выполнить самостоятельно:

Упр. 249(3, 4)

Упр. 250(3, 4)

У доски (на отворотах) работают 2 ученика.

Учащиеся, выполнившие работу раньше, чем на доске, проверяются и оцениваются учителем, а остальные -обмениваются тетрадями и проверяют работы друг друга.

Дополнительно: Упр. № 248 (1, 3)

7. Подведение итогов урока.

 Сегодня мы еще раз увидели, для чего же открыли квадратичную функцию и где можно использовать её график.

Надо помнить о том, что построение графика функции требует внимательности, аккуратности, точности в расчетах. Во всем нужен порядок. Да и математику затем учить следует, что она ум в порядок приводит.

8. Домашнее задание: §13 №249(1, 2), №250(1, 2), №248(2, 4).

9. Рефлексия: выходя из класса, оставьте на столе учителя одну из символов физиогностики, выражающее ваше состояние от урока.

Тема урока: Квадратичная функция. Функции вида y=ax 2 + n и y=a(x-m) 2 и их графики

Тема урока: Квадратичная функция. Функции вида y=ax 2 + n и y=a(x-m) 2 и их графики

Цели урока: Выработать умения строить графики функций вида y=ax 2 + n и y=a(x-m) 2 .

Вместо многоточия поставить пропущенные слова

1. Функция вида y= ax 2 + bx + c, где a,b,c- . . . , причем . . . 0, x-. . . , называется . . . функцией.

2. Функция y=x 2 – это функция y=ax 2 + . . .+. . . , при а=. . . , b=. . . , c=. . . .

3. Кривая, являющаяся графиком функции у=х 2 называется . . . .

4. Парабола у=х 2 касается оси ОХ в точке с координатами (. . .).

5. График функции у=х 2 симметричен относительно оси . . . .

6. Ось ОУ является осью . . . параболы.

7. При а . . . 0 ветви параболы у=ах 2 направлены вверх, а при а . . . 0-вниз.

Заполнить и сравнить данные таблицы

Таблица №1

х

у=х 2

-3

9

у=х ² +2

11

4

-2

-1

1

6

0

0

3

1

1

2

3

2

4

3

9

6

11

Таблица №2

х

0

у=(х-3) 2

9

1

2

4

3

1

4

0

5

1

6

4

9

0 или влево на ImI единиц при m   " width="640"

График функции у=а(х-m) 2 есть парабола, полученная из графика функции у=ах 2 в результате сдвига вправо вдоль оси абсцисс на m единиц при m0 или влево на ImI единиц при m