Цели урока:
Образовательные:
учить формулировать алгоритмы построения графиков квадратичных функций.
Развивающие:
развивать математическую зоркость и математическую речь, умение сравнивать, выделять характерные признаки, классифицировать;
Воспитательные:
формировать навыки сотрудничества, организации работы в группе, повышение мотивации изучения математики.
Задачи урока:
повторить основной материал, связанный с квадратичной функцией;
продолжить отработку и закрепление навыка построения графиков квадратичных функций с помощью таблицы;
создать условия (подвести) для учащихся к открытию ими алгоритмов построения графиков функций;
выявить уровень усвоения алгоритмов;
План урока.
1. Организационный момент. Учащиеся вместе с учителем строят параболу и выполняют ряд упражнений
Деление на группы по цвету стикера «Парабола» «Функция» « Аргумент»
2. Мотивация (каждая группа презентует свое название) игра «Внимание»
3. Проверка домашней работы (по готовым ответам).
Актуализация знаний:
Задание 1. Из данных функций выбрать те, которые являются квадратичными (соединить стрелками или вычеркнуть).
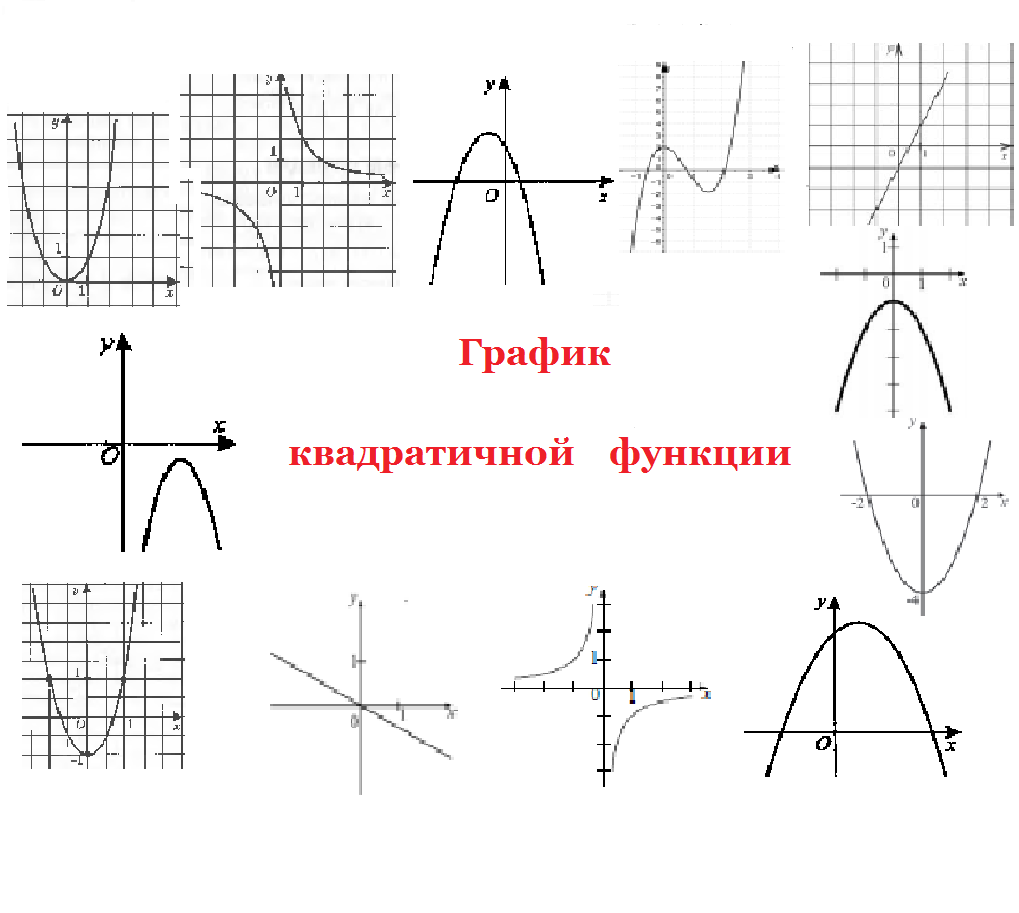
Задание 2. Из графиков функций, выбрать те, которые являются графиками квадратичной функции.
Задание 3. Назвать основные элементы параболы.
Задание 4. Определить направление ветвей
параболы по формуле, задающей функцию.
4. Практическая работа (лидеры проверяют)
5. Работа в группах.1) Установи соответствие и взаимопроверка
Группа 1 (Парабола) 2) Выполнение заданий на флипчарт бумаге.
Группы 2 и 3 (Функция» и Аргумент)
6. Анализ полученных результатов (презентация).
7. Домашнее задание. составить синквейн на тему квадратичная функция, из кусков параболы построить фигуры
8. Презентация « Парабола в архитектуре» Аманжолова Лаура
9. Рефлексия.
Ход урока.
1. Организационный момент:
Начать урок я хочу словами Конфуция о трёх путях ведущих к знаниям…..

Перед человеком к разуму три пути: путь размышления – это самый благородный путь, путь подражания – это самый лёгкий; путь личного опыта – это самый тяжёлый.
Я думаю, каждый из вас уже определил для себя свой путь к знанию и уровень, на котором вы будете сегодня работать.
Итак начнем.
На уроке можно ошибаться, сомневаться, консультироваться.
Если вам что-то непонятно помните: «Я всегда рядом».
2. Мотивация:
Сегодня мы с вами продолжим изучение одной из основных видов функций в курсе алгебры – квадратичной, поэтому каждая группа коротко расскажите о своем названии «Парабола» «Функция» « Аргумент»
Актуализация знаний:
А теперь повторим основные моменты, связанные с квадратичной функцией, которые нам сегодня пригодятся:
Сформулировать определение квадратичной функции;
Сформулировать свойства квадратичной функции у=ах2 при а>0, a<0.
Как из графика функции у=ах2 можно получить график функции у=ах2 + n; график функции у=а(х-m) 2
От чего зависит расположение вершины параболы?
Что может влиять на «ширину» параболы?
В каких случаях парабола пересекает ось абсцисс, касается ее или не пересекает?
Сколько достаточно знать точек, чтобы построить график любой квадратичной функции?
- Как называется график квадратичной функции? (парабола).
Задание 1.
Из данных функций выбрать те, которые являются квадратичными (соединить стрелками или вычеркнуть).
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход




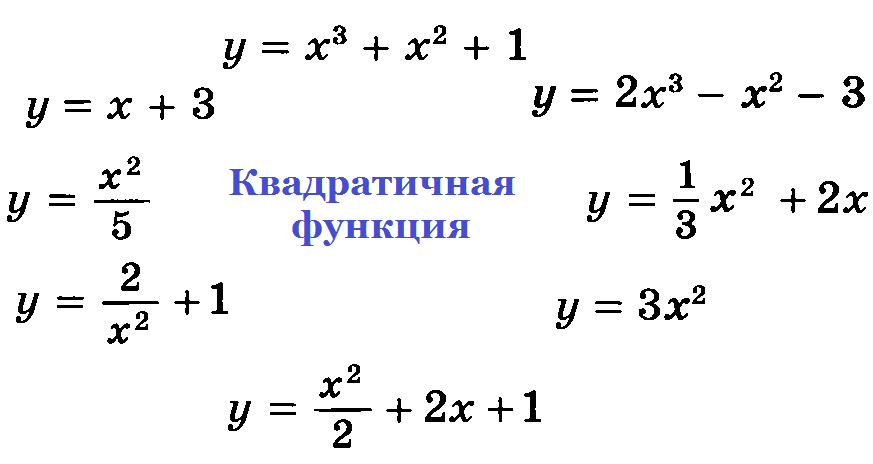















 Конспект урока по математике "Построение графика квадратичной функции с использованием сдвигов по осям координат" (0.63 MB)
Конспект урока по математике "Построение графика квадратичной функции с использованием сдвигов по осям координат" (0.63 MB)
 0
0 1436
1436 152
152 Нравится
0
Нравится
0


