Цель:
Научить строить «График функции у=ах2+вх+с», умение использовать алгоритм при построение графика.
Задачи:
- обучающие: закрепить знания, связанные с построением и исследованием графика квадратичной функции у=ах2+вх+с;
развивающие:
- способствоватьразвитию умений строить и исследовать графики квадратичной функции, анализировать, сравнивать, делать выводы;
- способствовать развитию познавательного интереса к предмету посредством использования ИКТ;
- воспитательные: способствовать формированию коммуникативной культуры, самостоятельности обучающихся.
Ход урока.
1. Стадия вызова.
Психологический настрой учащихся и создать благоприятную атмосферу в классе.
Тренинг видеоролик.
Формирование групп(при помощи координатной плоскости)
Проверка д/з.
№268, 269
1) m=-0,5
2) m=-0,5
3) m=-1
4) m=-4,5
Мозговой штурм
Какая функция называется квадратичной?
Определитекакие из данных функций являются квадратичными?
(укажите номер)
2. Осмысление содержание.
Построить квадратичную функцию без шаблонов, по алгоритму.
Свойства квадратичной функции?
Промежутки монотонности (возрастание и убывание функции)
Промежутки знакопостоянства у=у=ах2+вх+с
Наибольшее и наименьшее значение функции.
Что значит эти точки?
По какой формуле находится вершины парабола?
Математический диктант
Дана у=х2
Напишите уравнении квадратичной функции для каждого случая.
1. на 3ед. влево и на 2 ед. вверх
2. на 4ед. вправо и на 3ед.вниз
3. на 5ед. влево и на 5 ед. вниз
4. на 6ед. вправо и на 2ед. вверх
5. на 7ед. влево и на 1ед. вниз
Работа в паре
а) у = х2 – 4.
б) у = х2 – х,
у=0у=0
Задание.
Найти координаты вершины параболы
а) у(х)=х2-4х-5,
б) у(х)=-х2-2х+5.
Работа в группах
1. Найти нули квадратичной функции (мозаика)
(если они существуют).
1) у=х2+5х+6;
2) у=х2- 5х+4;
2. Найти координаты вершины параболы.
3) у=х2-10х+9;
4) у=х2-6х+8.
Построить график функции у=х2-4х+3.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход



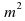 +bm+c.
+bm+c.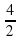 =2
=2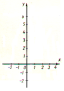 х=2- ур-е оси симметр.
х=2- ур-е оси симметр.








 Краткосрочное планирование урока по математике "Функция у=ах2+вх+с, ее свойства и график" (0.11 MB)
Краткосрочное планирование урока по математике "Функция у=ах2+вх+с, ее свойства и график" (0.11 MB)
 1
1 511
511 67
67 Нравится
0
Нравится
0


