
КОУ «Мартюшевская средняя общеобразовательная школа»
Тарского муниципального района
Согласовано: Утверждаю:
Заместитель директора по УВР Директор КОУ «Мартюшевская средняя
____________ / Н.Н.Щербак/ общеобразовательная школа» «___»__________2011г. ___________/Т.Н.Степанова/
Приказ № _от «__»_____________2011г.

2,5 час. в неделю, всего 85 часа
Учитель:Краснова Т.Н.
2013-2014учебный год

Пояснительная записка
Рабочая программа учебного курса алгебры и начал анализа для 10 класса составлена в соответствии с федеральным компонентом Государственного стандарта среднего (полного) общего образования на основе программы общеобразовательных учреждений: Алгебра и начала анализа 10-11 классы, - М.Просвещение, 2009, составитель Т.А.Бурмистрова.
Ориентировано на использование учебника «Алгебра и начала математического анализа : учеб. для 10 кл. общеобразоват. учреждений: базовый и профил. уровни/ С.М.Никольский, М.К.Потапов, Н.Н.Решетников, А.В.Шевкин]. –8-е изд., доп. М.:Просвещение, 2009. – 464 с.
Данная рабочая программа составлена для изучения алгебры и начал анализа в общеобразовательном классе на базовом уровне.
В федеральном компоненте базисного плана на изучение алгебры и начала анализа в 10 классе отведено 2,5 часа учебного времени в неделю, всего 85 часов.
Общая характеристика учебного предмета.
При изучении курса математики на базовом уровне продолжаются и получают развитие содержательные линии: «Алгебра», «Функции», «Уравнения и неравенства», «Геометрия», «Элементы комбинаторики, теории вероятностей, статистики и логики», вводится линия «Начала математического анализа».
Задачи учебного предмета
В рамках указанных содержательных линий решаются следующие задачи:
систематизация сведений о числах; изучение новых видов числовых выражений и формул; совершенствование практических навыков и вычислительной культуры, расширение и совершенствование алгебраического аппарата, сформированного в основной школе, и его применение к решению математических и нематематических задач;
расширение и систематизация общих сведений о функциях, пополнение класса изучаемых функций, иллюстрация широты применения функций для описания и изучения реальных зависимостей;
развитие представлений о вероятностно-статистических закономерностях в окружающем мире, совершенствование интеллектуальных и речевых умений путем обогащения математического языка, развития логического мышления.
Цели
Изучение математики в старшей школе на базовом уровне направлено на достижение следующих целей:
формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;
развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для обучения в высшей школе по соответствующей специальности, в будущей профессиональной деятельности;
овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения школьных естественнонаучных дисциплин на базовом уровне, для получения образования в областях, не требующих углубленной математической подготовки;
воспитание средствами математики культуры личности: отношения к математике как части общечеловеческой культуры: знакомство с историей развития математики, эволюцией математических идей, понимания значимости математики для общественного прогресса.
Общеучебные умения, навыки и способы деятельности
В ходе освоения содержания математического образования учащиеся овладевают разнообразными способами деятельности, приобретают и совершенствуют опыт:
построения и исследования математических моделей для описания и решения прикладных задач, задач из смежных дисциплин;
выполнения и самостоятельного составления алгоритмических предписаний и инструкций на математическом материале; выполнения расчетов практического характера; использования математических формул и самостоятельного составления формул на основе обобщения частных случаев и эксперимента;
самостоятельной работы с источниками информации, обобщения и систематизации полученной информации, интегрирования ее в личный опыт;
проведения доказательных рассуждений, логического обоснования выводов, различения доказанных и недоказанных утверждений, аргументированных и эмоционально убедительных суждений;
самостоятельной и коллективной деятельности, включения своих результатов в результаты работы группы, соотнесение своего мнения с мнением других участников учебного коллектива и мнением авторитетных источников.
Формы организации учебного процесса.
В данном классе ведущими методами обучения предмету являются: объяснительно-иллюстративный и репродуктивный, частично-поисковый. На уроках используются элементы следующих технологий: личностно ориентированное обучение, обучение с применением опорных схем, ИКТ.
При организации учебного процесса будет обеспечена последовательность изучения учебного материала: новые знания опираются на недавно пройденный материал; обеспечено поэтапное раскрытие тем с последующей реализацией; закрепление в процессе практикумов и деловых игр, тренингов; будут использоваться уроки – соревнования.
Основные типы учебных занятий:
урок изучения нового учебного материала,
урок закрепления изученного,
урок применения знаний;
урок обобщающего повторения и систематизации знаний;
урок контроля знаний и умений.
Основным типом урока является комбинированный.
Формы и средства контроля.
Формы контроля знаний, умений, навыков:
контрольная работа;
самостоятельная работа;
тесты;
устный опрос;
наблюдение;
беседа;
фронтальный опрос;
опрос в парах;
практикум;
Формы промежуточной и итоговой аттестации: контрольные работы, самостоятельные работы, тесты.
Итоговая аттестация предусмотрена в виде теста.
СОДЕРЖАНИЕ ТЕМ УЧЕБНОГО КУРСА .
1. Действительные числа (7 ч)
Понятие натурального числа. Множества чисел. Свойства действительных чисел. Перестановки. Размещения. Сочетания.
Основная цель — систематизировать известные и изучить новые сведения о действительных числах.
Знать понятие «Перестановки. Размещения. Сочетания»;
Уметь находить разницу между ними и научиться применять их при решении задач.
2. Рациональные уравнения и неравенства (12 ч )
Рациональные выражения. Формулы бинома Ньютона, суммы и разности степеней. Рациональные уравнения. Системы рациональных уравнений. Метод интервалов решения неравенств. Рациональные неравенства. Нестрогие неравенства. Системы рациональных неравенств.
Основная цель — сформировать умения решать рациональные уравнения и неравенства.
Знать формулы бинома Ньютона, и разности степеней.
Уметь решать рациональные уравнения и их системы; применять метод интервалов для решения несложных рациональных неравенств и их систем.
3. Корень степени n ( 6 ч )
Понятия функции и ее графика. Функция у = хn. Понятие корня степени n. Корни четной и нечетной степеней. Арифметический корень. Свойства корней степени n. Функция
у = 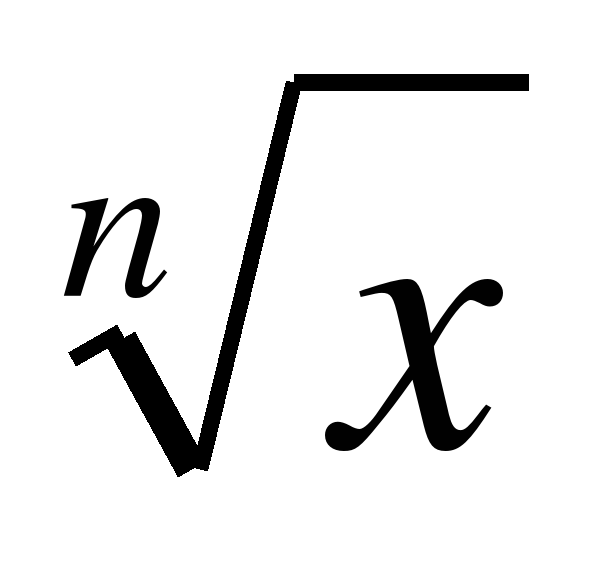 .
.
Основная цель — освоить понятия корня степени n и арифметического корня; выработать умение преобразовывать выражения, содержащие корни степени n.
Знать определение корня п-ой степени, понятие функции и ее графика, арифметического корня п-ой степени и его свойства.
Уметь находить значение корня на основе определения и свойств, выполнять преобразования выражений, содержащие корни, строить график функции у = 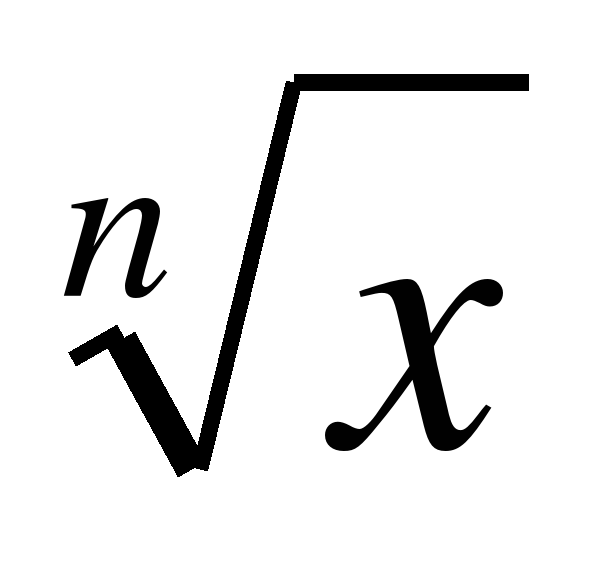 .
.
4. Степень положительного числа ( 8 ч )
Понятие и свойства степени с рациональным показателем. Предел последовательности.
Бесконечно убывающая геометрическая прогрессия. Число е.
Понятие степени с иррациональным показателем. Показательная функция.
Основная цель – усвоить понятие рациональной и иррациональной степеней положительного числа и показательной функции.
Знать определение степени с действительным показателем, определение показательной функции, формулу суммы бесконечной геометрической прогрессии;
уметь находить значение степени, упрощать выражения, содержащие степень, строить график показательной функции.
5. Логарифмы (5 ч)
Понятие и свойства логарифмов. Логарифмическая функция. Десятичный логарифм (приближенные вычисления). Степенные функции.
Основная цель — освоить понятия логарифма и логарифмической функции, выработать умение преобразовывать выражения, содержащие логарифмы.
Знать определение логарифма, свойства;
Уметь строить график логарифмической функции, находить значения логарифмических выражений, применять свойства логарифмов для преобразования логарифмических выражений.
6. Показательные и логарифмические уравнения и неравенства (7ч)
Простейшие показательные и логарифмические уравнения. Уравнения, сводящиеся к простейшим заменой неизвестного. Простейшие показательные и логарифмические неравенства. Неравенства, сводящиеся к простейшим заменой неизвестного.
Основная цель — сформировать умение решать показательные и логарифмические уравнения и неравенства.
Знать определение логарифмических и показательных уравнений и неравенств, приемы решения простейших их уравнений и неравенств;
уметь решать показательные и логарифмические уравнения и неравенства.
7. Синус и косинус угла (7 ч)
Понятие угла и его меры. Определение синуса и косинуса угла, основные формулы для них. Арксинус и арккосинус.
Основная цель — освоить понятия синуса и косинуса произвольного угла, изучить свойства функций угла: sin  и cos
и cos  .
.
Знать определение синуса, косинуса, радиана, арксинуса, арккосинуса, основные формулы тригонометрии;
Уметь выражать радианную меру угла в градусную и наоборот, находить значение синуса, косинуса любого угла, преобразовывать тригонометрические выражения, используя основные формулы, находить значения арксинусов и арккосинусов.
8. Тангенс и котангенс угла ( 4 ч )
Определения тангенса и котангенса угла и основные формулы для них. Арктангенс и арккотангенс.
Основная цель — освоить понятия тангенса и котангенса произвольного угла, изучить свойства функций угла: tg и ctg
и ctg .
.
Знать определение тангенса и котангенса, арктангенса и арккотангенса; основные формулы для них;
Уметь находить значения тангенса и котангенса любого угла.
9. Формулы сложения (7 ч )
Косинус суммы (и разности) двух углов. Формулы для дополнительных углов. Синус суммы (и разности) двух углов. Сумма и разность синусов и косинусов. Формулы для двойных и половинных углов.
Основная цель — освоить формулы косинуса и синуса суммы и разности двух углов, выработать умение выполнять тождественные преобразования тригонометрических выражений с использованием выведенных формул.
Знать формулы сложения, двойных и половинных углов, формулы суммы и разности синусов и косинусов;
Уметь применять формулы тригонометрии для упрощения тригонометрических выражений и вычислений .
10. Тригонометрические функции числового аргумента ( 5 ч )
Функции у = sin х , у = cos x, у = tg x, у = ctg x.
Основная цель — изучить свойства основных тригонометрических функций и их графиков.
Знать определение тригонометрических функций их свойства;
Уметь строить графики тригонометрических функций, определять их период.
11. Тригонометрические уравнения и неравенства ( 5 ч )
Простейшие тригонометрические уравнения. Тригонометрические уравнения, сводящиеся к простейшим заменой неизвестного. Применение основных тригонометрических формул для решения уравнений. Однородные уравнения.
Основная цель — сформировать умение решать тригонометрические уравнения и неравенства.
Знать формулы корней простейших тригонометрических уравнений, основные приемы решения тригонометрических уравнений;
Уметь решать простейшие тригонометрические уравнения.
12. Вероятность события ( 4 ч )
Понятие и свойства вероятности события.
Основная цель — овладеть классическим понятием вероятности события, изучить его свойства и научиться применять их при решении несложных задач.
13. Повторение курса алгебры и начал математического анализа (8ч)
| № п/п | Наименование разделов и тем | Количество часов |
| теория | контрольные работы |
| 1. | Действительные числа | 7 | - |
| 2. | Рациональные уравнения и неравенства | 11 | 1 |
| 3. | Корень степени n | 6 | - |
| 4. | Степень положительного числа | 7 | 1 |
| 5. | Логарифмы | 5 | - |
| 6. | Показательные и логарифмические уравнения и неравенства | 6 | 1 |
| 7. | Синус и косинус угла | 7 | - |
| 8 | Тангенс и котангенс угла | 3 | 1 |
| 9. | Формулы сложения | 7 | - |
| 10. | Тригонометрические функции числового аргумента | 4 | 1 |
| 11. | Тригонометрические уравнения и неравенства | 5 | - |
| 12. | Вероятность события | 4 | - |
| 13. | Повторение | 7 | 1 |
|
| ИТОГО. | 79 | 6 |
ТРЕБОВАНИЯ К УРОВНЮ
ПОДГОТОВКИ десятиклассников
В результате изучения математики на базовом уровне ученик должен
знать/понимать
значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;
вероятностный характер различных процессов окружающего мира.
Алгебра
уметь
выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;
вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства;
Функции и графики
уметь
определять значение функции по значению аргумента при различных способах задания функции;
строить графики изученных функций;
описывать по графику и в простейших случаях по формуле поведение и свойства функций;
решать графически уравнения;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Уравнения и неравенства
уметь
решать рациональные, показательные и логарифмические уравнения и неравенства, простейшие иррациональные и тригонометрические уравнения;
составлять уравнения и неравенства по условию задачи;
использовать для приближенного решения уравнений и неравенств графический метод;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Элементы комбинаторики, статистики и теории вероятностей
уметь
решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул;
вычислять в простейших случаях вероятности событий на основе подсчета числа исходов;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
анализа реальных числовых данных, представленных в виде диаграмм, графиков;
анализа информации статистического характера.
Перечень учебно-методических средств обучения.
Программы общеобразовательных учреждений. Алгебра и начала математического анализа 10-11 классы, - М.Просвещение, 2009, составитель Т.А.Бурмистрова
Алгебра и начала математического анализа. 10 класса: учеб.для общеобразоват. учреждений: базовый и профил. уровни /С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин. – 8-е изд.. – М.: Просвещение, 2009
Алгебра и начала математического анализа: дидакт. материалы для 10 класса: базовый и профил. уровни / М.К. Потапов, А.В. Шевкин. – 3-е изд. – М.: Просвещение, 2008
Алгебра и начала математического анализа. 10 класса: базовый и профил. Уровни: кн.для учителя/ М.К. Потапов, А.В. Шевкин. - М.: Просвещение, 2008
Календарно- тематическое планирование
10 класс
Алгебра и начала математического анализа по учебнику С.М. Никольского
2,5 часа в неделю, всего 85 часов.
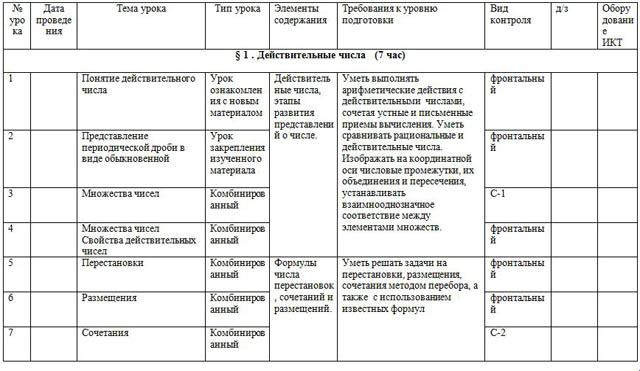
| № урока | Дата проведения | Тема урока | Тип урока | Элементы содержания | Требования к уровню подготовки | Вид контроля | д/з | Оборудование ИКТ |
|
| § 1 . Действительные числа (7 час)
|
|
| 1 |
| Понятие действительного числа | Урок ознакомления с новым материалом
| Действительные числа, этапы развития представлений о числе.
| Уметь выполнять арифметические действия с действительными числами, сочетая устные и письменные приемы вычисления. Уметь сравнивать рациональные и действительные числа. Изображать на координатной оси числовые промежутки, их объединения и пересечения, устанавливать взаимнооднозначное соответствие между элементами множеств. | фронтальный |
|
|
|
| 2 |
| Представление периодической дроби в виде обыкновенной | Урок закрепления изученного материала
| фронтальный |
|
|
|
| 3 |
| Множества чисел | Комбинированный
| С-1 |
|
|
|
| 4 |
| Множества чисел Свойства действительных чисел | Комбинированный
| фронтальный |
|
|
|
| 5 |
| Перестановки | Комбинированный
| Формулы числа перестановок, сочетаний и размещений. | Уметь решать задачи на перестановки, размещения, сочетания методом перебора, а также с использованием известных формул | фронтальный |
|
|
|
| 6 |
| Размещения | Комбинированный
| фронтальный |
|
|
|
| 7 |
| Сочетания | Комбинированный
| С-2 |
|
|
|
| §2. Рациональные уравнения и неравенства (12 час)
|
|
| 8 |
| Рациональные выражения | Комбинированный
| Формула бинома Ньютона. Свойства биноминальных коэффициентов. Треугольник Паскаля.
| Уметь выполнять арифметические действия с рациональными выражениями.
| фронтальный |
|
|
|
| 9 |
| Формулы бинома Ньютона, суммы и разности степеней
| Урок ознакомления с новым материалом
| Уметь раскладывать по формуле бинома Ньютона, находить коэффициент в разложении выражения по формуле бинома Ньютона, вычислять сумму коэффициентов | Мат.диктант |
|
|
|
| 10 |
| Рациональные уравнения | Комбинированный
| Решение рациональных уравнений с одним неизвестным. Решение систем рациональных уравнений с одним неизвестным. Основные приемы решения систем уравнений с одним неизвестным: подстановка, алгебраическое сложение, введение новых переменных.
|
Уметь: решать рациональные уравнения с одним неизвестным, их системы различными способами. Использовать для приближенного решения рациональных уравнений с одним неизвестным графический метод | практикум |
|
|
|
| 11 |
| Системы рациональных уравнений | Комбинированный
| фронтальный |
|
|
|
| 12 |
| Метод интервалов решения неравенств | Комбинированный
| Метод интервалов. Решение рациональных неравенств и систем рациональных неравенств с одним неизвестным |
Уметь решать рациональные неравенства с одним неизвестным методом интервалов. Уметь решать рациональные неравенства и их системы с одним неизвестным. Использовать для приближенного решения неравенств с одним неизвестным графический метод.
| С-4 |
|
|
|
| 13 |
| Рациональные неравенства | Комбинированный
| фронтальный |
|
|
|
| 14 |
| Решение рациональных неравенств | Закрепление знаний и способов деятельности | практикум |
|
|
|
| 15 |
| Нестрогие неравенства | Комбинированный
| фронтальный |
|
|
|
| 16 |
| Решение нестрогих неравенств | Закрепление знаний и способов деятельности | С-5 |
|
|
|
| 17 |
| Системы рациональных неравенств | Комбинированный
| фронтальный |
|
|
|
| 18 |
| Решение задач по теме «Рациональные неравенства» | Урок обобщения и систематизации | практикум |
|
|
|
| 19 |
| Контрольная работа №1 по теме «Рациональные уравнения и неравенства» | Урок проверки и коррекции знаний и умений | К-1 |
|
|
|
| §3 Корень степени n (6 час)
|
|
| 20 |
| Работа над ошибками. Функция и её график | Комбинированный урок
| Функция. Область определения и множества значений. График функции. Построение графиков функций заданных различными способами. Свойства функций. Функция y = x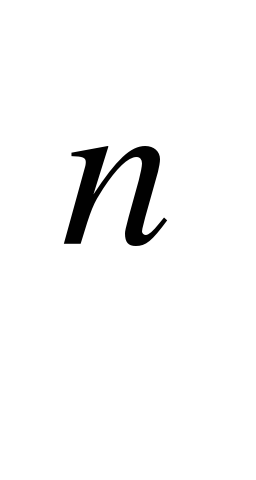 , ее график и свойства , ее график и свойства
|
Уметь определять значение функции по значению аргумента при различных способах задания функции. Строить график функции y = x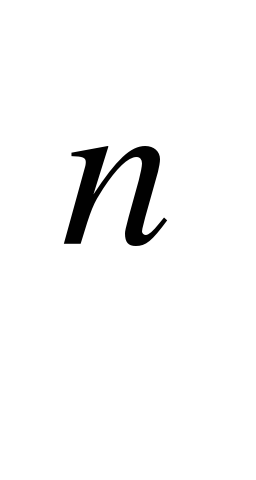 . Описывать по графику поведение и свойства функции. . Описывать по графику поведение и свойства функции.
| фронтальный |
|
|
|
| 21 |
| Функция у = хn | Комбинированный урок
| С-6 |
|
|
|
| 22 |
| Понятие корня степени n | Комбинированный урок
| фронтальный |
|
|
|
| 23 |
| Корни четной и нечетной степени | Комбинированный урок
| Корень степени n1 и его свойства.
|
Уметь находить значение корня натуральной степени, используя свойства корней степени n.
| фронтальный |
|
|
|
| 24 |
| Арифметический корень | Комбинированный урок
|
| фронтальный |
|
|
|
| 25 |
| Свойства корней степени n | Комбинированный урок
|
| Мат.диктант |
|
|
|
| § 4 . Степень положительного числа. ( 8 час)
|
|
| 26 |
|
Понятие степени с рациональным показателем | Комбинированный урок
| Степень с рациональным показателем и ее свойства | Уметь находить значение корня с рациональным показателем.
| фронтальный |
|
|
|
| 27 |
| Свойства степени с рац. показателем | Комбинированный урок
|
|
| C-8 |
|
|
|
| 28 |
| Понятие предела последовательности | Урок ознакомления с новым материалом
| Понятие о пределе последовательности. |
Иметь понятия о бесконечно малой и бесконечно большей величинах. Уметь находить предел числовой последовательности, используя свойства пределов.
| фронтальный |
|
|
|
| 29 |
| Бесконечно убывающая геометрическая прогрессия | Урок ознакомления с новым материалом
| Бесконечно убывающая геометрическая прогрессия и ее сумма | С-9 |
|
|
|
| 30 |
| Число е | Урок ознакомления с новым материалом
| Число е. | фронтальный |
|
|
|
| 31 |
| Понятие степени с иррациональным показателем | Урок ознакомления с новым материалом
| Понятие о степени с действительным показателем. Свойства степени с действительным показателем.
| Иметь представление о степени с действительным показателем.
| фронтальный |
|
|
|
| 32 |
| Показательная функция | Комбинированный урок
| Показательная функция. Ее свойства и график | Уметь определять значение функции по значению аргумента при различных способах задания функции. Строить график. Описывать по графику поведение и свойства функций | фронтальный |
|
|
|
| 33 |
| Контрольная работа №3 по теме: «Степень положительного числа» | Урок проверки и коррекции знаний и умений |
|
| К-3 |
|
|
|
| §5 Логарифмы (5 час)
|
|
| 34 |
| Работа над ошибками. Понятие логарифма
| Урок ознакомления с новым материалом
| Логарифм числа. Десятичные и натуральные логарифмы. Основное логарифмическое тождество.
|
Уметь находить значения логарифма. Уметь выполнять преобразования выражений, содержащих логарифмы.
| фронтальный |
|
|
|
| 35 |
| Вычисление логарифма
| Закрепление знаний и способов деятельности |
| практикум |
|
|
|
| 36 |
| Свойства логарифма
| Урок ознакомления с новым материалом
| Логарифм произведения, частного, степени, переход к новому основанию.
| Мат.диктант |
|
|
|
| 37 |
| Вычисление логарифмов, применяя свойства | Закрепление знаний и способов деятельности |
| Дифференцированные задания |
|
|
|
| 38 |
| Логарифмическая функция
| Урок ознакомления с новым материалом
| Логарифмическая функция. Ее свойства и график | Уметь определять значение функции по значению аргумента при различных способах задания функции. Строить график. Описывать по графику поведение и свойства функций. | фронтальный |
|
|
|
| §6. Показательные и логарифмические уравнения и неравенства (7 час)
|
|
| 39 |
| Простейшие показательные уравнения | Комбинированный урок
| Показательные и логарифмические неравенства. |
Уметь решать простейшие показательные и логарифмические уравнения и неравенства; уравнения и неравенства, сводящиеся к простейшим заменой неизвестного. | фронтальный |
|
|
|
| 40 |
| Простейшие логарифмические уравнения | Комбинированный урок
|
| практикум |
|
|
|
| 41 |
| Уравнения, сводящиеся к простейшим заменой неизвестного | Комбинированный урок
|
| фронтальный |
|
|
|
| 42 |
| Простейшие показательные неравенства | Комбинированный урок
|
| С-10 |
|
|
|
| 43 |
| Простейшие логарифмические неравенства | Комбинированный урок
|
| фронтальный |
|
|
|
| 44 |
| Неравенства, сводящиеся к простейшим заменой неизвестного | Комбинированный урок
|
| практикум |
|
|
|
| 45 |
| Контрольная работа № 4 по теме: «Показательные и логарифмические уравнения и неравенства» | Урок проверки и коррекции знаний и умений |
| К-4 |
|
|
|
| §7 Синус и косинус угла (7 час)
|
|
|
|
|
| фронтальный |
| 46 |
| Работа над ошибками. Понятие угла | Урок ознакомления с новым материалом
| Синус, косинус, произвольного угла. Основные тригонометрические тождества. Формулы приведения. Основные формулы для синуса и косинуса угла. Арксинус, арккосинус. Преобразование простейших тригонометрических выражений |
Знать понятие синуса и косинуса угла. Уметь выполнять тождественные преобразования тригонометрических выражений, используя основные формулы для синуса и косинуса угла.
| фронтальный |
|
|
|
| 47 |
| Радианная мера угла | Комбинированный урок
| фронтальный |
|
|
|
| 48 |
| Определение синуса и косинуса угла | Комбинированный урок
| фронтальный |
|
|
|
| 49 |
| Основные формулы для синуса и косинуса угла | Комбинированный урок
| фронтальный |
|
|
|
| 50 |
| Решение задач, используя основные формулы для синуса и косинуса угла | Урок применения знаний и умений
| Мат.диктант |
|
|
|
| 51 |
| Арксинус | Урок ознакомления с новым материалом | С-11 |
|
|
|
| 52 |
| Арккосинус | Урок ознакомления с новым материалом
| фронтальный |
|
|
|
| §8. Тангенс и котангенс угла (4 час)
|
|
|
|
|
| фронтальный |
| 53 |
| Определение тангенса и котангенса угла | Комбинированный урок
| Тангенс, котангенс произвольного угла. Формулы приведения. Тангенс суммы и разности двух углов. Основные формулы для тангенса и котангенса угла. Арктангенс, арккотангенс. Преобразование простейших тригонометрических выражений |
Уметь выполнять тождественные преобразования тригонометрических выражений, используя основные формулы для тангенса и котангенса угла.
| фронтальный |
|
|
|
| 54 |
| Основные формулы для тангенса и котангенса угла | Комбинированный урок
| Мат.диктант |
|
|
|
| 55 |
|
Арктангенс
| Комбинированный урок
| фронтальный |
|
|
|
| 56 |
| Контрольная работа №5 «Тригонометрические формулы»
| Урок проверки и коррекции знаний и умений
| К-5 |
|
|
|
| §9. Формулы сложения. (7 час)
|
|
|
|
|
| С-16 |
| 57 |
| Работа над ошибками. Косинус разности и косинус суммы двух углов | Комбинированный урок
| Косинус суммы и косинус разности двух углов. Синус, косинус и тангенс суммы и разности двух углов. |
Уметь проводить преобразования выражений содержащих тригонометрические функции. | фронтальный |
|
|
|
| 58 |
| Формулы для дополнительных углов | Комбинированный урок
| С-12 |
|
|
|
| 59 |
| Синус суммы и синус разности двух углов | Комбинированный урок
| фронтальный |
|
|
|
| 60 |
| Сумма и разность синусов и косинусов | Комбинированный урок
| фронтальный |
|
|
|
| 61 |
| Формулы для двойных и половинных углов |
| Синус и косинус двойного угла. Формулы половинного угла. | фронтальный |
|
|
|
|
62 |
| Произведение синусов и косинусов |
| Преобразование сумм тригонометрических функций в произведение и произведения в сумму. |
Уметь проводить преобразования выражений содержащих тригонометрические функции. | фронтальный |
|
|
|
| 63 |
| Формулы для тангенсов |
|
|
| С-14 |
|
|
|
| §10. Тригонометрические функции числового аргумента ( 5 час )
|
|
|
|
|
| С-18 |
| 64 |
| Функция у=sinх. | Урок ознакомления с новым материалом
| Тригонометрические функции, их свойства и графики. Периодичность, основной период. |
Уметь выполнять построения графиков тригонометрических функций, описывать по графику поведение и свойства функций.
| фронтальный |
|
|
|
| 65 |
| Функция у=cosх. | Урок ознакомления с новым материалом
| фронтальный |
|
|
|
| 66 |
| Функция у=tgх. | Урок ознакомления с новым материалом
|
|
|
|
|
| 67 |
| Функция у=ctgх. | Урок ознакомления с новым материалом
|
|
| фронтальный |
|
|
|
| 68 |
| Контрольная работа № 6 по теме «Формулы сложения. Тригонометрические функции» | Урок проверки и коррекции знаний и умений
|
|
| К-6 |
|
|
|
| §11. Тригонометрические уравнения и неравенства ( 5 час ) |
|
| 69 |
| Работа над ошибками Простейшие тригонометрические уравнения. | Урок ознакомления с новым материалом
| Решение тригонометрических уравнений. Использование свойств и графиков функций при решении уравнений.
|
Уметь решать простейшие тригонометрические уравнения, уравнения, сводящиеся к простейшим заменой неизвестного. Использовать для приближенного решения тригонометрических уравнений графический метод.
| фронтальный
|
|
|
|
| 70 |
| Решение простейших тригонометрических уравнений. | Урок закрепления изученного
| практикум |
|
|
|
| 71 |
| Уравнения, сводящиеся к простейшим заменой неизвестного. | Урок ознакомления с новым материалом
| практикум |
|
|
|
| 72 |
| Применение основных тригонометрических формул для решения уравнений. | Урок закрепления изученного
| С-16 |
|
|
|
| 73 |
| Однородные уравнения. |
Урок ознакомления с новым материалом | фронтальный
|
|
|
|
| §12. Вероятность события (4час) |
|
| 74 |
|
Понятие вероятности события | Урок ознакомления с новым материалом
| Элементарные и сложные события. Рассмотрение случаев и вероятность суммы несовместных событий, вероятность противоположного события. Понятие о независимости событий. Решение практических задач с применением вероятностных методов. |
Вычислять в простейших случаях вероятности событий на основе подсчета числа исходов. Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: анализа реальных числовых данных, представленных в виде диаграмм, графиков. | фронтальный
|
|
|
|
| 75 |
| Вероятность события. Закрепление | Урок закрепления изученного
| фронтальный
|
|
|
|
| 76 |
| Свойства вероятностей | Урок ознакомления с новым материалом
| практикум |
|
|
|
| 77 |
| Решение практических задач с применением вероятностных методов. | Урок закрепления изученного
| С-17 |
|
|
|
| Повторение ( 8 ч ) |
|
| 78 |
| Рациональные уравнения и неравенства | Урок обобщения и систематизации знаний
|
| Уметь выполнять задания по данной теме. | практикум |
|
|
|
| 79 |
| Корень степени п | Урок обобщения и систематизации знаний
|
| Уметь выполнять задания по данной теме. | практикум |
|
|
|
| 80 |
| Логарифмы | Урок обобщения и систематизации знаний
|
| Уметь выполнять задания по данной теме. | практикум |
|
|
|
| 81 |
| Показательные и логарифмические уравнения и неравенства | Урок обобщения и систематизации знаний
|
| Уметь выполнять задания по данной теме. | практикум |
|
|
|
| 82 |
| Тригонометрические функции | Урок обобщения и систематизации знаний
|
| Уметь выполнять задания по данной теме. | практикум |
|
|
|
| 83 |
| Тригонометрические уравнения и неравенства | Урок обобщения и систематизации знаний
|
| Уметь выполнять задания по данной теме. | практикум |
|
|
|
| 84 |
| Итоговая контрольная работа № 8 |
|
|
| Итоговый тест |
|
|
|
| 85 |
| Работа над ошибками. Итоговое занятие |
|
|
|
|
|
|
|

 Получите свидетельство
Получите свидетельство Вход
Вход












 КТП по алгебре (10 класс) (0.35 MB)
КТП по алгебре (10 класс) (0.35 MB)
 0
0 2453
2453 446
446 Нравится
0
Нравится
0








