Координатная плоскость (презентация)

Как определяется местоположение фигуры на игровом поле?

А где еще в жизни можно встретится с подобными примерами?

(отметка в школьном журнале на пересечении Ф. И. ученика и даты проведения урока, отметка в школьном дневнике на пересечении названия урока и столбца «Оценка», график дежурств, школьное расписание)

Как правильно занять место в кинозале?

С помощью координатной сетки летчики, моряки определяют местоположение объектов.

Более чем за 100 лет до н.э греческий ученый Гиппарх предложил опоясать на карте земной шар параллелями и меридианами и ввести теперь хорошо известные географические координаты: широту и долготу и обозначить их числами.

Рене Декарт (1596-1650) французский философ, естествоиспытатель, математик.

Целью Декарта было описание природы при помощи математических законов.

Автор координатной плоскости, поэтому ее часто называют декартовой системой координат.

Координатная прямая или координатная ось (ось x) - прямая на которой выбраны:

- начальная точка О (начало отсчета),

- масштаб (единичный отрезок, т.е отрезок, длина которого считается равной 1)

- положительное направление.

Как вы думаете о чем будет наш урок?

Каждая клетка на игровом поле определяется

двумя координатами - буквой и цифрой

Как определяется местоположение фигуры на игровом поле?

А где еще в жизни можно встретится с подобными примерами?

(отметка в школьном журнале на пересечении Ф.И. ученика и даты проведения урока, отметка в школьном дневнике на пересечении названия урока и столбца «Оценка», график дежурств, школьное расписание)

Где еще в жизни можно встретиться с подобными примера использования координат?

Как правильно занять место в кинозале?

Чтобы правильно занять свое место, в кинотеатре нужно знать две координаты – ряд и место

С помощью координатной сетки летчики, моряки определяют местоположение объектов;

Как давно системы координат пронизывают практическую жизнь человека?

Более чем за 100 лет до н.э греческий ученый Гиппарх предложил опоясать на карте земной шар параллелями и меридианами и ввести теперь хорошо известные географические координаты : широту и долготу и обозначить их числами.

Более чем за 100 лет до н.э греческий ученый Гиппарх предложил опоясать на карте земной шар параллелями и меридианами и ввести теперь хорошо известные географические координаты: широту и долготу и обозначить их числами.

Рене Декарт (1596-1650) французский философ, естествоиспытатель, математик. Целью Декарта было описание природы при помощи математических законов. Автор координатной плоскости , поэтому ее часто называют декартовой системой координат.

Рене Декарт (1596-1650) - французский философ, естествоиспытатель, математик. Целью Декарта было описание природы при помощи математических законов. Автор координатной плоскости, поэтому ее часто называют декартовой системой координат.

НО перед тем как поговорить о прямоугольной Декартовой системе координат, вспомним координатную прямую.

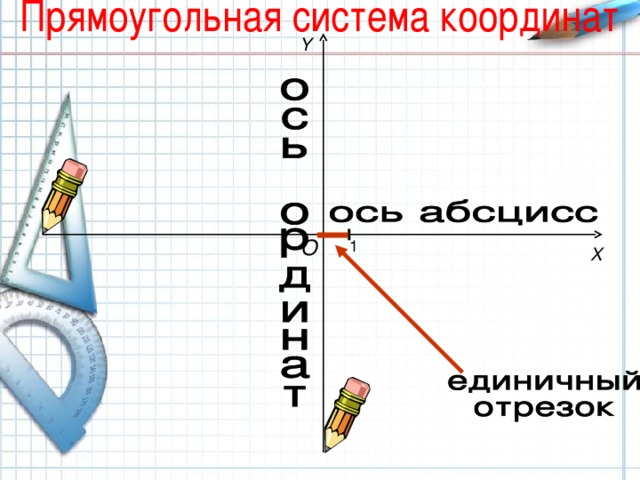
Координатная прямая или координатная ось (ось x ) -

- прямая на которой выбраны:

• начальная точка О ( начало отсчета ),
• масштаб ( единичный отрезок , т.е отрезок, длина которого считается равной 1)
• положительное направление.

х

1

0

Y

О

1

X

При изучении темы «Координатная прямая», вы научились находить по координате положение точки на прямой. А как указать положение точки на плоскости? Для этого нам понадобиться координатная плоскость . Рассмотрим ее составляющие:

          две перпендикулярные прямые - оси координат (часто называют  - прямоугольная система координат)

          вертикальная - ось абсцисса (х), горизонтальная -ось ордината(у), стрелки осей указывают положительные направления,

          начало координат -  точка пересечения прямых

9

Y

Каждая точка на координатной плоскости имеет свой точный адрес. Это пара чисел ( щелчок): первое число по оси OX , второе – по оси OY . Эти числа называются координатами точки.

Чтобы не путать порядок следования координат, вспомните, как устроены наши дома (щелчок): сначала (щелчок) мы заходим в нужный подъезд (по оси OX) , а затем поднимаемся на нужный этаж (по оси OY) .

О

X

9

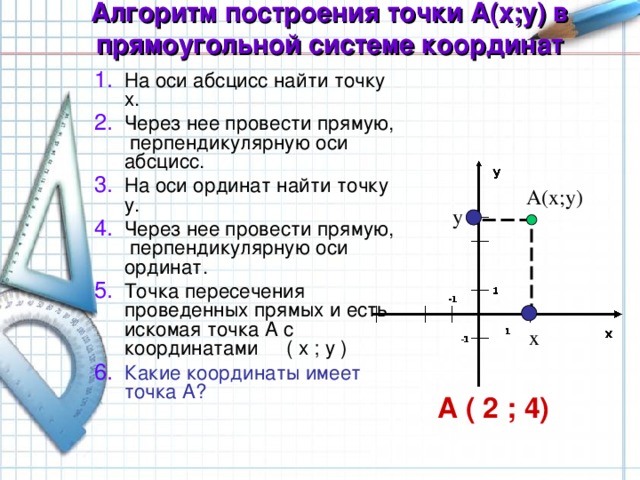
Алгоритм построения точки А(х;у) в прямоугольной системе координат

• На оси абсцисс найти точку х.
• Через нее провести прямую, перпендикулярную оси абсцисс.
• На оси ординат найти точку у.
• Через нее провести прямую, перпендикулярную оси ординат.
• Точка пересечения проведенных прямых и есть искомая точка A с координатами ( х ; у )
• Какие координаты имеет точка A ?

А( x;y )

y

x

А ( 2 ; 4 )

Индивидуальные задания

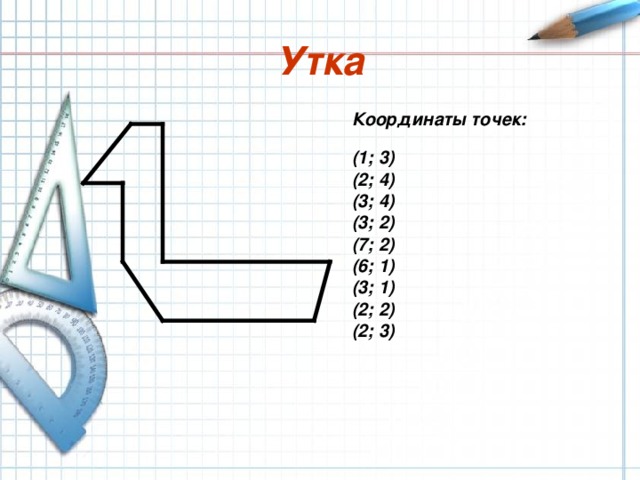
Утка

Координаты точек:

(1; 3)

(2; 4)

(3; 4)

(3; 2)

(7; 2)

(6; 1)

(3; 1)

(2; 2)

(2; 3)

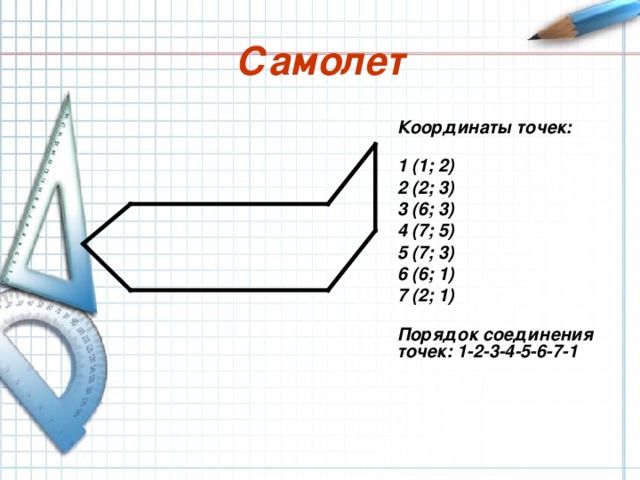
Самолет

Координаты точек:

1 (1; 2)

2 (2; 3)

3 (6; 3)

4 (7; 5)

5 (7; 3)

6 (6; 1)

7 (2; 1)

Порядок соединения точек: 1-2-3-4-5-6-7-1

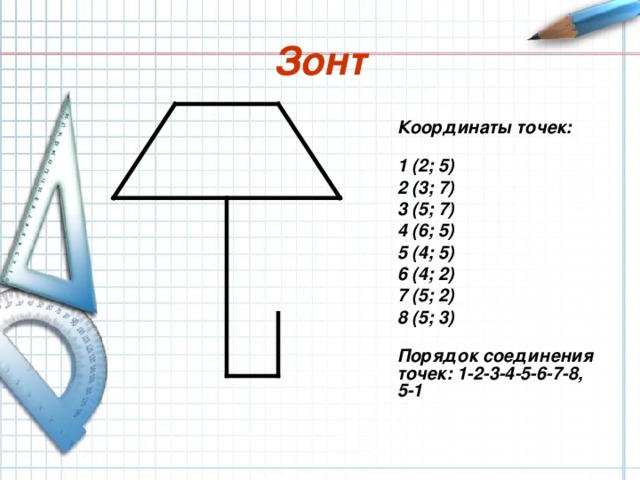
Зонт

Координаты точек:

1 (2; 5)

2 (3; 7)

3 (5; 7)

4 (6; 5)

5 (4; 5)

6 (4; 2)

7 (5; 2)

8 (5; 3)

Порядок соединения точек: 1-2-3-4-5-6-7-8, 5-1

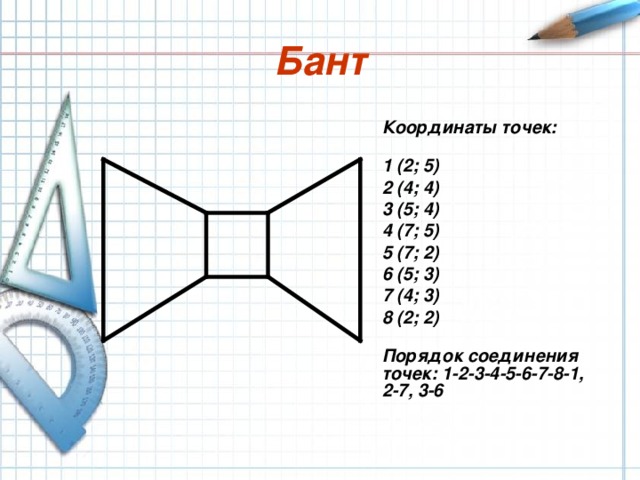
Бант

Координаты точек:

1 (2; 5)

2 (4; 4)

3 (5; 4)

4 (7; 5)

5 (7; 2)

6 (5; 3)

7 (4; 3)

8 (2; 2)

Порядок соединения точек: 1-2-3-4-5-6-7-8-1, 2-7, 3-6

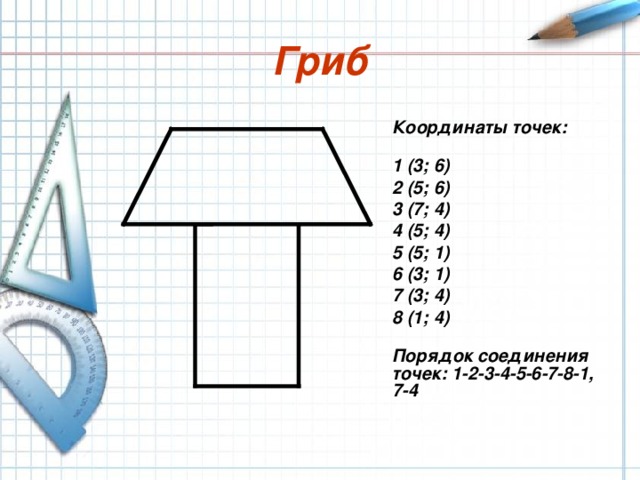
Гриб

Координаты точек:

1 (3; 6)

2 (5; 6)

3 (7; 4)

4 (5; 4)

5 (5; 1)

6 (3; 1)

7 (3; 4)

8 (1; 4)

Порядок соединения точек: 1-2-3-4-5-6-7-8-1, 7-4

Y

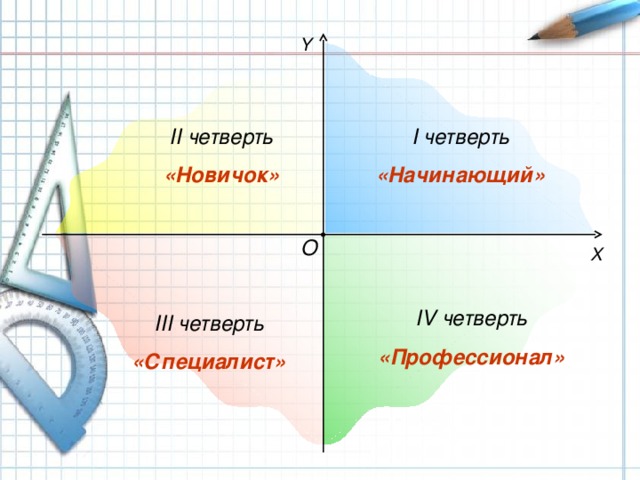
II четверть

I четверть

«Новичок»

«Начинающий»

О

X

IV четверть

«Профессионал»

Оси координат разбивают плоскость на четыре части, которые называются координатными четвертями

III четверть

«Специалист»

18

Цель: научить учащихся строить точки по заданным её координатам и определять координаты точки, отмеченной на координатной плоскости

Задачи:

• ознакомить учащихся с прямоугольной системой координат на плоскости;
• научить свободно ориентироваться на координатной плоскости;
• хорошо воспринимать на слух координаты;
• четко и аккуратно выполнять геометрические построения;
• развивать творческие способности;
• активизировать внимание учащихся с помощью применения мультимедийных средств;
• воспитывать интерес к предмету и ответственность за общий результат

Рене Декарт

Гиппарх

Птолемей

О

с

ь

о

р

д

и

н

а

т

У

Начало отсчета

4

3

2

Х

-1

5

4

-2

2

-5

-3

1

-4

3

1

0

Ось абсцисс

-1

-2

-3

-4

Система географических координат

широта – параллели, долгота -меридианы

А

1

нейн

2

Б

-е

Гла

В

3

Оди

Г

ние

4

шо

алу

едл

яцх

авне

5

оги.

нза

йца

яжа

6

ое ур

цаф

юут

яза

гон

Ли

адв

чше.

оро

вно

Восстанови текст (не забудь разделить текст на слова): В5, А1, Г3, А4, В1

Линейное уравнение

Ученикам предлагается создать свое звездное небо.

На приготовленной черной бумаге отмечена система координат. Желтые звездочки, приготовленные заранее, клеят на черную бумагу, по заданным координатам созвездий.

Созвездие “Персея”: (-5;-3), (-2;-2), (0;-1), (2;-2), (4;-1), (5;0), (6;2), (1;1), (1;3). Созвездие “Цефея”: (0;5), (-1;4), (-2;1), (1;-1), (6;-1), (3;2). Созвездие “Андромеды”: (-2;9), (0;7), (1;4), (2;-2), (-2;5), (-4;4). Созвездие “Кассиопеи”: (-5;0), (-3;2), (-1;0), (1;0), (3;-2) и другие созвездия.

Все полученные работы дети вешают на большое черное полотно, в результате получается звездное небо.

Это Аусеклис - или утренняя звезда . Один из самых популярных знаков в латышской орнаментике. Считалось, что аусеклис может уберечь от всего плохого , поэтому его чертили на земле, закладывая дом, рисовали на дверях хлева, старались иметь в одежде. Магическая сила аусеклиса защищала от наваждения, какие бы формы оно не принимало. Но все эти свойства аусеклиса проявлялись только тогда, когда он был нарисован правильно – одним движением, не отрывая карандаша от листа бумаги. Попробуйте сделать это дома

Расшифруйте слово, используя координатную плоскость с буквами

При астрономических наблюдениях координатная сетка накладывается на небесный свод с Землей в центре.

3 группа:

ваше задание

• подумайте и по готовому чертежу определить , что необходимо сделать, чтобы рисунок изменил направление .
• затем выпишите координаты только тех точек , которые изменили свое положение на координатной плоскости.

(7;7)

(11;4)

(7;1)

(7;7)

(11;4)

(7;1)

Y

Сегодня я узнал что …

Больше всего мне понравилось …

О

X

Мне было сложно …

Я могу описать урок одним словом …

32