Кому нужна теорема Пифагора?!

В работе на втором слайде должен присутствовать видеофрагмент из программы Ералаш.

Все остальные слайды раскрывают смысл практического применения теоремы Пифагора и позволяют обучающимся занятся вполне реальными самостоятельными проектами.

Кому нужна

теорема Пифагора?!

Вставляется фрагмент Ералаша

о теореме Пифагора

Мобильная связь

Какую наибольшую высоту должна иметь антенна мобильного оператора, чтобы передачу можно было принимать в радиусе

R=200 км?

Радиус Земли равен 6380 км.

Решение:

Пусть AB= x , BC=R=200 км , OC=r=6380км.

OB=OA+AB, OB=r + x.

Используя теорему Пифагора , получим

OB 2 =r 2 + BC 2 =40744400

OB =6382,3

АВ=6382,3 – 6380=2,3 км

Ответ: 2,3 км.

Молниеотвод

Известно, что молниеотвод защищает от молнии все предметы, расстояние которых от его основания не превышает его удвоенной высоты.

Необходимо определить оптимальное положение молниеотвода на двускатной крыше, обеспечивающее наименьшую его доступную высоту.

Решение:

По теореме Пифагора

h 2 ≥ a 2 +b 2 ,

значит h м ≥ ( V a 2 +b 2 ):2

Вид на дом сверху

Собор Парижской Богоматери

Архитектура

В зданиях готического и романского стиля верхние части окон расчленяются каменными ребрами, которые не только играют роль орнамента, но и способствуют прочности окон.

На рисунке представлен простой пример такого окна в готическом стиле. Способ построения его очень прост.

Из рисунка легко найти центры шести дуг окружностей, радиусы которых равны ширине окна (b) для наружных дуг, половине ширины (b/2) для внутренних дуг. Остается еще полная окружность, касающаяся четырех дуг. Ее радиус равен b/4. Тогда становится ясным и положение ее центра.

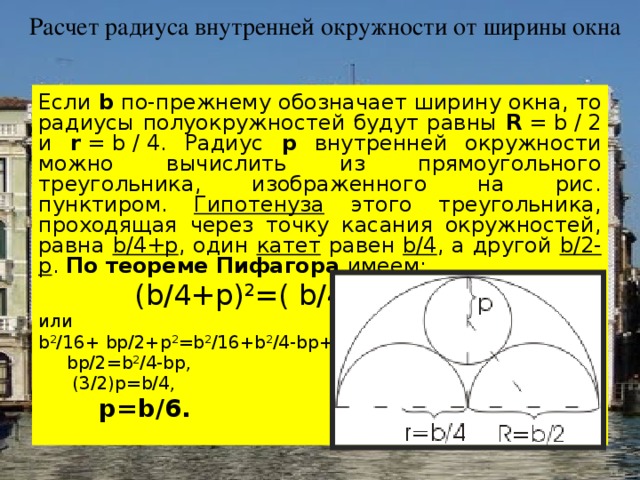
Расчет радиуса внутренней окружности от ширины окна

Если b по-прежнему обозначает ширину окна, то радиусы полуокружностей будут равны R  = b / 2 и r  = b / 4. Радиус p внутренней окружности можно вычислить из прямоугольного треугольника, изображенного на рис. пунктиром. Гипотенуза этого треугольника, проходящая через точку касания окружностей, равна b/4+p , один катет равен b/4 , а другой b/2-p . По теореме Пифагора имеем:

(b/4+p) 2 =( b/4) 2 +( b/2-p) 2

или

b 2 /16+ bp/2+p 2 =b 2 /16+b 2 /4-bp+p 2 ,

bp/2=b 2 /4-bp,

(3/2)p=b/4,

p=b/6.

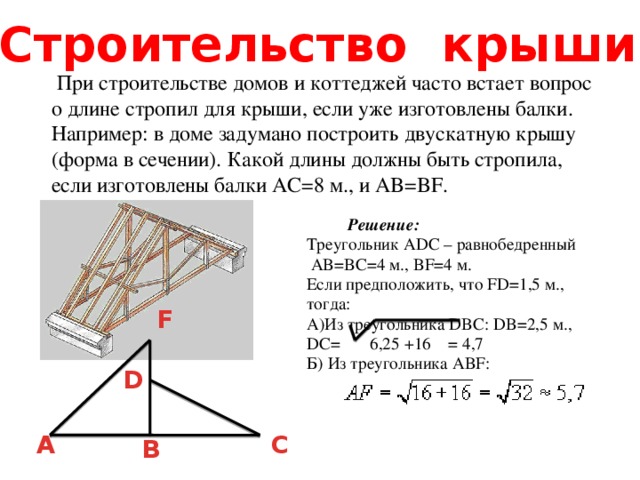
Строительство крыши

  При строительстве домов и коттеджей часто встает вопрос о длине стропил для крыши, если уже изготовлены балки. Например: в доме задумано построить двускатную крышу (форма в сечении). Какой длины должны быть стропила, если изготовлены балки AC=8 м., и AB=BF.

         Решение:

Треугольник ADC – равнобедренный

AB=BC=4 м., BF=4 м.

Если предположить, что FD=1,5 м.,

тогда:

А)Из треугольника DBC: DB=2,5 м.,

DС= 6,25 +16 = 4,7

Б) Из треугольника ABF:

F

При строительстве домов и коттеджей часто встает вопрос о длине стропил для крыши, если уже изготовлены балки.

D

А

C

B

7

Немного о марсианах

В конце девятнадцатого века высказывались разнообразные предположения о существовании обитателей Марса подобных человеку. В шутку, хотя и не совсем безосновательно, было решено передать обитателям Марса сигнал в виде теоремы Пифагора.

Неизвестно, как это сделать! Но для всех очевидно, что математический факт, выражаемый теоремой Пифагора, имеет место всюду и поэтому похожие на нас обитатели другого мира должны понять такой сигнал.

Пифагорова теорема

Не знаю, чем кончу поэму И как мне печаль избыть: Древнейшую теорему Никак я не в силах забыть.

Стоит треугольник как ментор, И угол прямой в нем есть, И всем его элементам Повсюду почет и честь.

Прелестная гипотенуза Взнеслась так смело в высь! И с нею в вечном союзе Два катета тоже взнелись.

Она царит на квадратах, И песню поет она; Та песня влечет куда-то Геометров древних волна.

И все на торжищах света, Как в огненном кольце, И все повторяют это: а 2 , b 2 , с!

И даже в холодной медузе Огонь эта песня зажгла, И все это гипотенузы И катетов двух дела!

Г. Вебер