Итоговая контрольная работа по геометрии 9 класс
Вариант 1
Часть 1
-
В треугольнике ABC BM – медиана и BH – высота. Известно, что AМ=36 и BC=BM. Найдите AH.
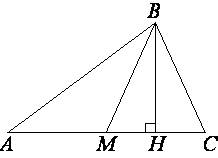
-
Боковая сторона трапеции равна 13, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 12 и 16.
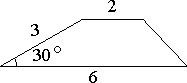
-
Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=103∘ и ∠OAB=24∘. Найдите угол BCO. Ответ дайте в градусах.
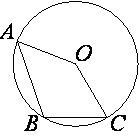
-
Прямые m и n параллельны. Найдите ∠3, если ∠1=440, ∠2=780. Ответ дайте в градусах.
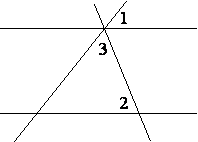
-
Около прямоугольника, стороны которого 7дм и 9дм, описана окружность. Найдите длину этой окружности.
-
Найдите меньший угол равнобедренной трапеции, если два ее угла относятся как 1:2. Ответ дайте в градусах.
-
Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 45°. Найдите площадь параллелограмма, делённую на
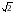
-
На рисунке изображен параллелограмм. Используя рисунок, найдите sinBDC.
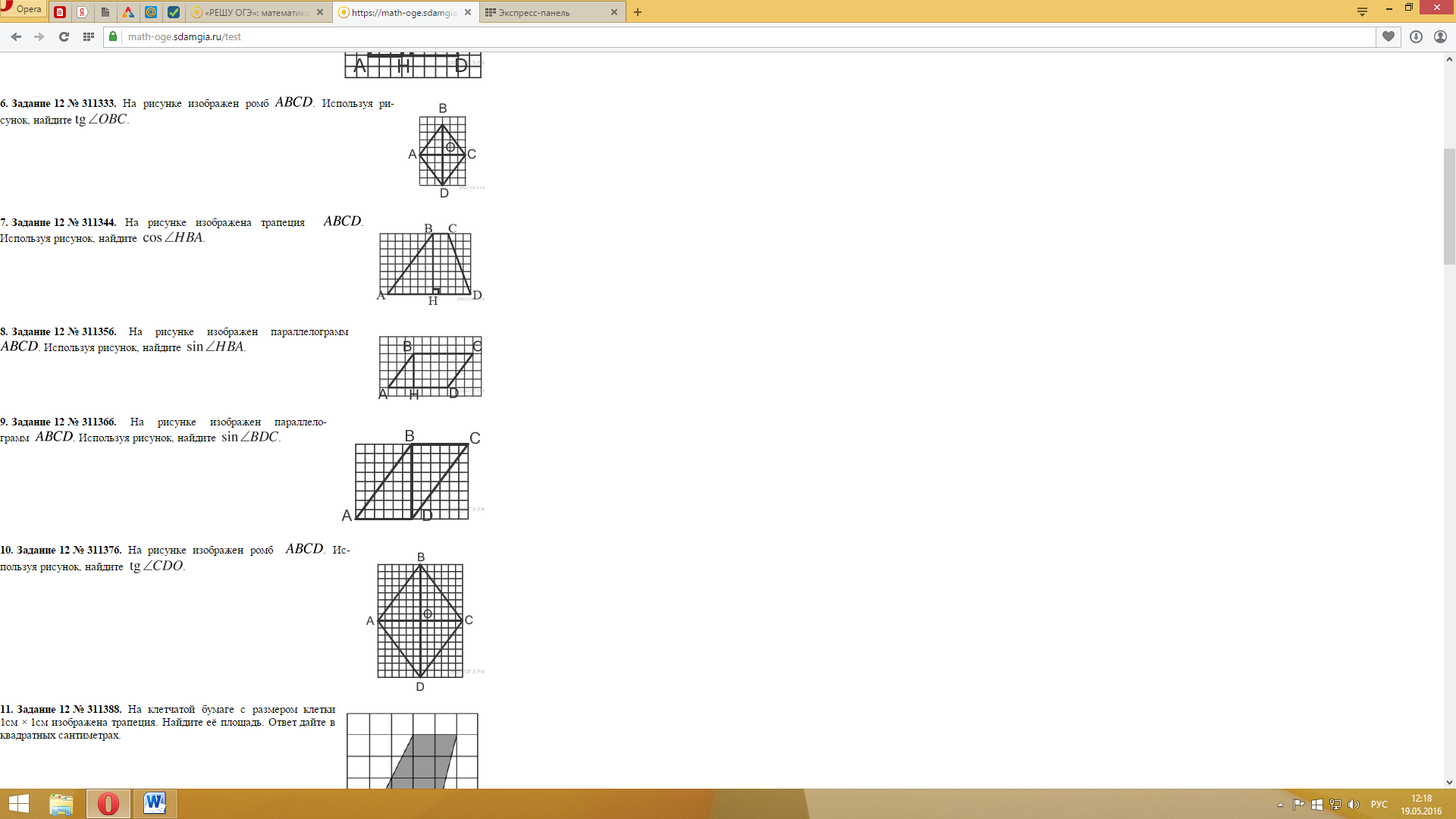
-
Выберите верные утверждения:
-
Биссектриса треугольника делит его сторону на отрезки, пропорциональные двум другим сторонам.
-
Отношение площадей подобных треугольников равно коэффициенту подобия.
-
Гипотенуза прямоугольного треугольника меньше катета.
-
Медианы треугольника пересекаются в одной точке вне треугольника.
-
Высота, проведённая из вершины прямого угла к гипотенузе, является средним пропорциональным между катетами прямоугольного треугольника.
-
Площадь трапеции равна произведению полусуммы оснований на высоту.
-
Из точки А проведены две касательные к окружности с центром в точке О. Радиус окружности равен 10 см, угол между касательными равен 60°. Найти расстояние от точки А до точки О.
Часть 2
-
На окружности с центром O отмечены точки A и B так, что ∠AOB = 66°. Длина меньшей дуги AB равна 99. Найдите длину большей дуги.
-
Биссектриса угла A параллелограмма ABCD пересекает сторону ВС в точке Е. Найдите периметр параллелограмма, если AD=12 см, а ВЕ=5 см.
-
Две стороны треугольника равны 5 см и 16 см, а угол между ними 1200. Найдите третью сторону треугольника и его площадь.
Итоговая контрольная работа по геометрии 9 класс
Вариант 2
Часть 1
-
В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=64 и BC=BM. Найдите AH.

-
В равнобедренной трапеции основания равны 2 и 8, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
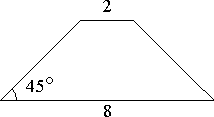
-
В окружности с центром в точке О проведены диаметры AD и BC, угол OAB равен 65°. Найдите величину угла OCD.
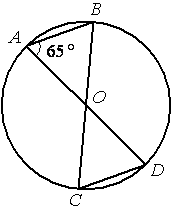
-
Прямые m и n параллельны. Найдите ∠3, если ∠1=480, ∠2=620. Ответ дайте в градусах.

-
Прямоугольник, стороны которого 3 м и 4 м, вписан в круг. Найдите площадь круга.
-
Найдите угол ABC равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной CD углы, равные 30° и 80° соответственно.
-
Периметр квадрата равен
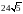 . Найдите площадь этого квадрата.
. Найдите площадь этого квадрата. -
Одна из сторон параллелограмма равна 12, другая равна 5, а синус одного из углов равен 1/3. Найдите площадь параллелограмма.
-
На рисунке изображен ромб. Используя рисунок, найдите tgCDO

-
Выберите верные утверждения:
-
Вокруг любого треугольника можно описать окружность.
-
Квадрат касательной равен произведению отрезков секущей, на которые её делит окружность.
-
Площади подобных треугольников относятся как коэффициент подобия.
-
Диагонали параллелограмма делят его на четыре равных треугольника.
-
Площадь ромба равна произведению его диагоналей.
-
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Часть 2
-
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 6.
-
Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите BC, если AB=36.
-
Две стороны треугольника равны 5 см и 24 см, а угол между ними 600. Найдите третью сторону треугольника и его площадь.
Промежуточная аттестация по математике (геометрия) 9 класс
Итоговый тест
Инструкция по выполнению работы
На выполнение теста дается 45 минут. Работа состоит из двух частей, включающих в себя 13 заданий.
Часть 1 содержит 10 заданий с кратким ответом базового уровня по материалу курса геометрии. Ответом является целое число или конечная десятичная дробь.
Часть 2 содержит 3 более сложных задания по материалу курса геометрии. При их выполнении надо записать полное обоснованное решение и ответ.
При выполнении работы разрешается использовать линейку, циркуль. Использование калькулятора не допускается.
Задания можно выполнять в любом порядке. Текст задания переписывать не надо, необходимо только указать его номер.
За каждое правильно выполненное задание части1 выставляется 1 балл. Задания части 2 расположены по нарастанию сложности и оцениваются в 2,3,4 балла.
Максимальное количество баллов: 19
Критерии оценивания: «5» - 15 -19 баллов
«4» - 11 -14 баллов
«3» - 5 -10 баллов
Желаем успеха!
| №/№ | Вариант 1 | Вариант 2 |
| | 27 | 48 |
| | 91 | 15 |
| | 79 | 65 |
| | 58 | 70 |
| |
| 6,25 |
| | 60 | 110 |
| | 2,5 | 4 |
| | 0,6 | 20 |
| | 156 | 0,75 |
| | 20 | 126 |
| | 441 | 3 |
| | 34 | 72 |
| | a=19 S= | a= S= |

 Получите свидетельство
Получите свидетельство Вход
Вход




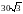









 Итоговая контрольная работа по геометрии 9 класс (314.45 KB)
Итоговая контрольная работа по геометрии 9 класс (314.45 KB)
 0
0 6136
6136 364
364 Нравится
0
Нравится
0


