Формы мышления.

Формы мышления. Алгебра высказываний. Логические выражения и таблицы истинности.

• Первые учения о формах и способах  рассуждений  возникли  в странах Древнего Востока (Китай, Индия), но в основе современной логики лежат учения, созданные в 4 веке до нашей эры  древне-греческими мыслителями.
• Основы формальной логики заложил Аристотель,  который впервые отделил логические формы речи от ее  содержания.  Он исследовал терминологию логики, подробно разобрал теорию умозаключений и доказательств, описал ряд логических операций, сформулировал основные законы мышления.
•       Логика  изучает  внутреннюю  структуру  процесса мышления, который реализуется в  таких  естественно  сложившихся формах как понятие, суждение, умозаключение и доказательство .

Формы мышления

Понятие

Понятие - это форма мышления, отражающая наиболее существенные свойства  предмета, отличающие его от других предметов.

В структуре каждого понятия нужно различать две стороны: содержание и объем.

Содержание понятия составляет совокупность существенных признаков предмета. Объем понятия определяется совокупностью предметов, на  которую оно распространяется.

Высказывание.  

• Высказывание (суждение) - это форма мышления, выраженная с помощью понятий, посредством которой что-либо утверждают или отрицают о предметах, их свойствах и отношениях между ними.
• Высказывание может быть  истинным  или  ложным . Истинным будет суждение, в котором связь понятий правильно отражает свойства  и отношения реальных вещей. Ложным суждение будет в том случае,  когда  связь  понятий искажает объективные отношения, не соответствует  реальной  действительности.
• В естественном языке высказывания  выражаются  повествовательными предложениями. Высказывание не может быть  выражено  повелительным  или  вопросительным предложением. Высказывания могут выражаться с помощью математических,  физических, химических и прочих знаков.
• Высказывание называется  простым , если никакая его часть сама не является высказыванием. Высказывание, состоящее из простых высказываний, называются  составным  (сложным).

Умозаключение.

•   Умозаключение - это форма мышления, посредством которой из одного или нескольких суждений, называемых посылками , по определенным правилам логического вывода получается новое знание о предметах реального  мира ( вывод ).
• Умозаключения  бывают дедуктивные, индуктивные и по аналогии .      В дедуктивных умозаключениях рассуждения ведутся от общего к частному. Например, из двух суждений: «Все металлы  электропроводны» и «Ртуть является металлом» путем умозаключения можно сделать вывод, что: «Ртуть электропроводна».
• В индуктивных умозаключениях рассуждения ведутся от частного к общему. Например, установив, что отдельные металлы -  железо, медь, цинк, алюминий и т.д. - обладают свойством  электропроводности, можно сделать вывод, что все металлы  электропроводны.
•   Умозаключение по аналогии представляет собой движение мысли от общности одних свойств и отношений у сравниваемых  предметов или процессов к общности других свойств и отношений. Например, химический состав Солнца и Земли сходен по  многим  показателям, поэтому, когда на Солнце обнаружили неизвестный еще на Земле химический элемент гелий, то по аналогии заключили: такой  элемент есть и на Земле.

Доказательство.

•   Доказательство есть мыслительный процесс,  направленный  на подтверждение или опровержение какого-либо положения посредством других несомненных, ранее обоснованных доводов.  
• Доказательство по своей логической форме  не отличается от умозаключения. Однако, если в умозаключении  заранее исходят из истинности посылок и следят только за правильностью логического вывода, в доказательстве подвергается логической проверке истинность самих посылок.

Алгебра высказываний

• Алгебра  в широком смысле этого слова  наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться над различными математическими объектами (алгебра переменных и функций, алгебра векторов, алгебра множеств и т.д.).
• Объектами алгебры логики являются высказывания.
• Алгебра логики отвлекается от смысловой содержательности высказываний.  Ее интересует только один факт — истинно или ложно данное высказывание, что дает возможность определять истинность или ложность составных высказываний алгебраическими методами.
• Простые высказывания  в алгебре логики обозначаются  заглавными  латинскими буквами:

А  = {Аристотель - основоположник логики}

В  = {На яблонях растут бананы}.

• Истинному высказыванию ставится в соответствие 1, ложному — 0. Таким образом,  А  = 1,  В  = 0.
• Составные высказывания на естественном языке образуются с помощью союзов, которые в алгебре высказываний заменяются на логические операции. Логические операции задаются таблицами истинности

Логическая операция КОНЪЮНКЦИЯ (логическое умножение) :

·  в естественном языке соответствует союзу  и ;

·  в алгебре высказываний обозначение  &,^ ;

·  в языках программирования обозначение  And .

• Конъюнкция - это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.

А

В

0

0

0

А^В

1

0

1

0

0

1

1

0

1

Логическая операция ДИЗЪЮНКЦИЯ (логическое сложение) :

·    в естественном языке соответствует союзу  или ;

·    обозначение V  ;

·    в языках программирования обозначение  Or .

• Дизъюнкция - это логическая операция, которая каждым двум простым высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны  и  истинным,  когда хотя бы одно из двух образующих его высказываний истинно.

А

В

0

АVВ

0

0

1

1

0

1

0

1

1

1

1

Логическая операция ИНВЕРСИЯ (отрицание) :

в естественном языке соответствует словам  неверно, что...  и частице  не ;

·  обозначение ¬,¯  ;

·  в языках программирования обозначение  Not ;

• Отрицание - это логическая операция, которая каждому простому высказыванию ставит в соответствие  составное  высказывание, заключающееся в том, что исходное высказывание отрицается.

А

¬А

0

1

1

0

Логическая операция ИМПЛИКАЦИЯ (логическое следование) :

·     в естественном языке соответствует обороту   если ..., то ... ;

·     обозначение   .

• Импликация - это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно.

А

А

В

В

0

0

0

0

0

0

А   В

1

1

1

1

1

1

1

0

1

1

0

1

1

1

0

0

1

1

·       в естественном языке соответствует оборотам речи  тогда и только тогда;   в том и только в том случае ;

·       обозначения   ,  ~  .

• Эквивалентность – это логическая операция,  ставящая  в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны. 

Логическая операция ЭКВИВАЛЕНТНОСТЬ (равнозначность) :

А

А

В

В

0

0

0

0

0

0

АВ

1

1

1

1

1

1

0

0

1

1

0

0

1

1

0

0

1

1

Логические выражения и таблицы истинности

• Таблицу, показывающую,  какие значения принимает составное высказывание при  всех сочетаниях (наборах)  значений  входящих в него простых высказываний,  называют  таблицей истинности  составного высказывания.
• Составные высказывания в алгебре логики записываются с помощью логических выражений. Для любого логического выражения достаточно просто построить таблицу истинности.

Логические выражения и таблицы истинности

• Алгоритм построения  таблицы  истинности:
• 1)       подсчитать количество переменных  n  в логическом выражении;
• 2)       определить число строк в таблице, которое равно  m =  2 n ;
• 3)       подсчитать количество логических операций в логическом выражении и определить количество столбцов в таблице, которое равно  количеству переменных  плюс  количество операций;
• 4)       ввести названия столбцов таблицы в соответствии с последовательностью выполнения логических операций с учетом скобок и приоритетов;
• 5)       заполнить стобцы входных переменных наборами значений;
• 6)       провести заполнение таблицы истинности по столбцам,  выполняя логические операции в соответствии с установленной  в  п.4  последовательностью.

Логические выражения и таблицы истинности

• Наборы входных переменных, во избежание ошибок, рекомендуют перечислять следующим образом:
• а)       разделить колонку значений первой переменной пополам и заполнить верхнюю часть колонки нулями, а нижнюю единицами;
• б)       разделить колонку  значений  второй переменной на четыре части и заполнить каждую четверть чередующимися группами нулей и единиц , начиная с группы нулей;
• в)       продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами нулей или единиц до тех пор, пока группы нулей и единиц не будут состоять из одного символа.

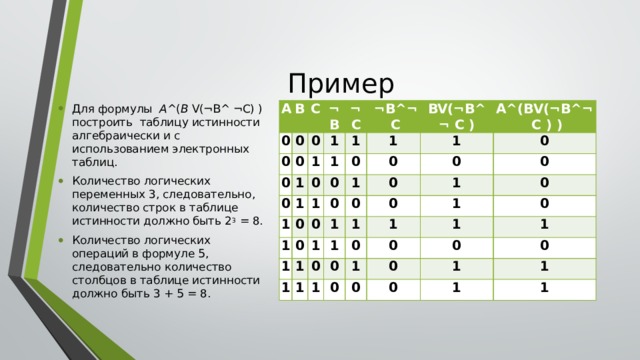
Пример

• Для формулы   A ^( B  V(¬B^ ¬C) ) построить  таблицу истинности алгебраически и с использованием электронных таблиц.
• Количество логических переменных 3, следовательно, количество строк в таблице истинности должно быть 2 3  = 8.
• Количество логических операций в формуле 5, следовательно количество столбцов в таблице истинности должно быть 3 + 5 = 8.

A

0

B

0

C

0

¬B

0

0

0

1

1

¬C

1

0

0

1

1

1

1

  ¬B^¬ C

0

1

0

0

BV(¬B^¬ C )

1

1

0

0

1

0

A^(BV(¬B^¬ C ) )

0

1

1

0

1

1

0

0

1

1

0

0

1

1

0

1

0

1

0

0

1

1

0

1

0

1

1

0

0

1

0

0

0

0

1

0

1

1

1

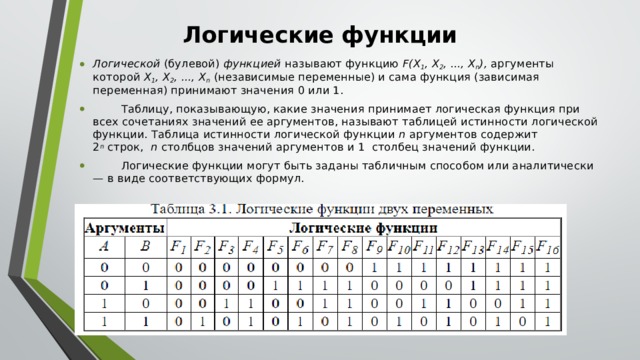
Логические функции

• Логической  (булевой)  функцией  называют функцию  F(Х 1 , Х 2 , ..., Х n ),  аргументы которой  Х 1 , Х 2 , ..., Х n  (независимые переменные) и сама функция (зависимая переменная) принимают значения 0 или 1.
•         Таблицу, показывающую, какие значения принимает логическая функция при всех сочетаниях значений ее аргументов, называют таблицей истинности логической функции. Таблица истинности логической функции  n  аргументов содержит 2 n  строк,   n  столбцов значений аргументов и 1  столбец значений функции.
•         Логические функции могут быть заданы табличным способом или аналитически — в виде соответствующих формул.

Логические законы и правила преобразования логических выражений

1. Закон двойного отрицания:

А =¬¬A.

Двойное отрицание исключает отрицание.

2.  Переместительный (коммутативный) закон :

— для логического сложения:

АVB = BVA ;

— для логического умножения:

A ^ B  =  B ^ A .

Логические законы и правила преобразования логических выражений

3.  Сочетательный (ассоциативный)  закон:

— для логического сложения:

( A  V B ) V C  =  A  V ( B  V C );

— для логического умножения:

( A ^ B )^ C  =  A ^( B ^ C ).

При одинаковых знаках скобки можно ставить произвольно или вообще опускать.

4.  Распределительный (дистрибутивный) закон :

— для логического сложения:

(AV B)^C  = (A^C) V(B^C);

— для логического умножения:

( A ^ B ) V C  = ( A V  C )^( B V  C ).

Определяет правило выноса общего высказывания за скобку.

Логические законы и правила преобразования логических выражений

5. Закон общей инверсии (законы де Моргана):

— для логического сложения

¬(AVB)=¬A^¬B;

— для логического умножения:

¬(A^B)=¬AV¬B

Логические законы и правила преобразования логических выражений

6. Закон идемпотентности ( от латинских слов idem — тот же самый и potens —сильный; дословно — равносильный):

— для логического сложения:

A V A = A ;

— для логического умножения:

A ^ A = A .

Закон означает отсутствие показателей степени.

7. Законы исключения констант:

— для логического сложения:

AV 1 = 1, A V0 = A ;

— для логического умножения:

A ^1 = A , A ^0 = 0.

Логические законы и правила преобразования логических выражений

8. Закон противоречия:

A^¬A = 0.

Невозможно, чтобы противоречащие высказывания были одновременно истинными.

9. Закон исключения третьего :

A Ú¬A= 1.

Из двух противоречащих высказываний об одном и том же предмете одно всегда истинно, а второе — ложно, третьего не дано.

Логические законы и правила преобразования логических выражений

10. Закон поглощения :

— для логического сложения:

A V( A ^ B ) = A ;

— для логического умножения:

A ^( A V B ) = A .

11.  Закон исключения (склеивания ):

— для логического сложения:

( A ^ B )V(¬A^ B ) = B ;

— для логического умножения:

( A V B )^(¬AV B ) = B .

Контрольные вопросы и задания

• Назовите основные формы мышления. Дайте им определения и приведите примеры
• Что изучает алгебра высказываний?
• Дайте определения для конъюнкции, дизъюнкции, инверсии.
• Дайте определения для эквивалентности и импликации.
• Сформулируйте основные логические законы
• Сформулируйте алгоритм построения таблицы истинности