Элементы теории игр

Элементы теории игр

• «симметричная» стратегия
• игра НИМ
• игра ЦЗЯНЬШИЦЗЫ

Теория игр — раздел математики, предметом которого является анализ принятия оптимальных решений в условиях конфликта.

Возникнув из задач классической теории вероятностей, теория игр превратилась в самостоятельный раздел

в 1945-1955.

Таким образом, теория игр — один из новейших разделов математики.

Под игрой понимается процесс, в котором участвуют две и более сторон, ведущих борьбу за реализацию своих интересов. Каждая из сторон имеет свою цель и использует собственную стратегию, разработанную с учетом представлений этой стороны о других участниках, их ресурсах и их возможных стратегиях.

В математических играх существуют понятия выигрышной стратегии , то есть набора правил (можно сказать, инструкции или алгоритма) следуя которым, один из игроков обязательно выиграет (не зависимо от того, как играет его соперник) и ничейной стратегии , следуя которой один из игроков обязательно добьётся либо выигрыша, либо ничьей.

В любой математической игре существует либо выигрышная стратегия для одного из игроков, либо ничейные стратегии для обоих (если игра допускает ничью). В зависимости от этого игра называется выигрышной для первого или второго игрока,

или ничейной.

Например крестики–нолики (на доске 3×3) являются ничейной игрой. К какому из перечисленных случаев относятся шахматы и шашки неизвестно. Хотя стратегия (либо выигрышная, либо ничейная) в этих играх существует, она не найдена, поэтому соревнования по этим играм пока представляют интерес.

Задача 1: В двух кучках лежат предметы, по 100 предметов в каждой. За ход разрешается взять произвольное количество предметов, но только из одной кучки. Проигрывает тот, кто не может сделать очередной ход. Найдите выигрышную стратегию для второго игрока

Второму игроку достаточно повторять ходы первого, но только в другой кучке. Таким образом, только после ходов второго в количество предметов в кучках становится равным, следовательно, ситуация, когда в обеих кучках не останется ни одного предмета, также может наступить только после хода второго, а, значит, он не проиграет. Поскольку с каждым ходом количество предметов в кучках уменьшается, игра закончится, и так как второй не проиграет – он выиграет.

Задача 2: В трёх кучках лежат предметы, по 100 предметов в каждой. За ход разрешается взять произвольное количество предметов, но только из одной кучки. Проигрывает тот, кто не может сделать очередной ход. Найдите выигрышную стратегию для первого игрока.

Забирая все предметы из одной кучки, первый сводит игру к игре «две кучки по 100», в которой он играет уже вторым.

Задача 3: Два миллионера по очереди кладут пятаки на круглый стол, так, чтобы они не накладывались друг на друга. Проигрывает тот, кто не может сделать хода. Как надо играть миллионеру, который кладёт первый пятак, чтобы наверняка выиграть?

Выигрывает первый . Первый ход – положить пятак в центр стола, и дальше симметрия.

Задача 4: Двое по очереди разламывают шоколадку. За один ход разрешается сделать прямолинейный разлом любого из имеющихся кусков вдоль углубления. Проигрывает тот, кто первым отломит дольку 1 × 1. Кто выигрывает при правильной игре, если шоколадка имеет размеры а) 10 × 10; б) 10 × 13. в) шоколадка 10 × 13, но первый получивший дольку 1 × 1 выигрывает.

Всюду выигрывает второй , разделив шоколадку на две, и далее действуя симметрично. В пункте в)  надо играть симметрично до предпоследнего момента

Задача 5: Двое по очереди ставят шахматных слонов в клетки доски 8 × 8 так, чтобы слоны не били друг друга. Проигрывает тот, кто не может сделать ход. Кто выигрывает при правильной игре, и как ему при этом нужно играть?

Выигрывает второй . Симметрия относительно вертикальной оси или относительно центра.

Задача 6: У ромашки а) 12 лепестков; б) 11 лепестков. За ход разрешается оторвать либо один лепесток, либо два рядом растущих лепестка. Проигрывает тот, кто не может сделать хода.

В обоих случаях выигрывает второй . Своим первым ходом он разбивает лепестки на две одинаковых группы, а дальше действовать симметрично. В а) проходит и тривиальная центрально-симметричная стратегия.

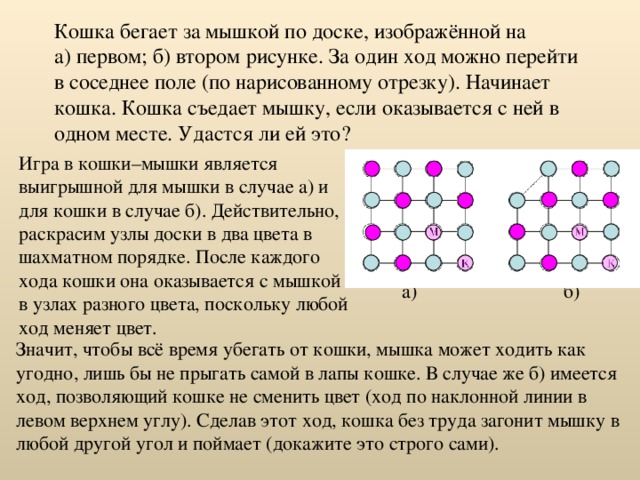
Кошка бегает за мышкой по доске, изображённой на а) первом; б) втором рисунке. За один ход можно перейти в соседнее поле (по нарисованному отрезку). Начинает кошка. Кошка съедает мышку, если оказывается с ней в одном месте. Удастся ли ей это?

Игра в кошки–мышки является выигрышной для мышки в случае а) и для кошки в случае б). Действительно, раскрасим узлы доски в два цвета в шахматном порядке. После каждого хода кошки она оказывается с мышкой в узлах разного цвета, поскольку любой ход меняет цвет.

б)

а)

Значит, чтобы всё время убегать от кошки, мышка может ходить как угодно, лишь бы не прыгать самой в лапы кошке. В случае же б) имеется ход, позволяющий кошке не сменить цвет (ход по наклонной линии в левом верхнем углу). Сделав этот ход, кошка без труда загонит мышку в любой другой угол и поймает (докажите это строго сами).

=2 ) выигрышны для начинающего " width="640"

Игра НИМ . На столе лежит 3 кучки спичек. Двое играющих поочередно берут спички из этих кучек, причем за один ход играющий может взять любое число спичек из одной кучки. Выигравшим считается тот, кто возьмет последнюю спичку.

Обозначим количество спичек в кучках а , b и c соответственно. а b c - положение (позиция) на данный момент.

Позиция 0,1,1 проигрышная для начинающего.

Своим ходом он обязан взять одну спичку, тогда соперник забирает вторую и выигрывает.

Задача : определить, при каких начальных положениях начинающий может выиграть, а при каких нет, и указать метод правильной (беспроигрышной) игры.

Все остальные положения 0, 1, С (где с =2 ) выигрышны для начинающего

=2 ) выигрышны для начинающего Своим первым ходом он берет с-1 спичку из третьей кучки, оставляя противнику заведомо проигрышную позицию 0,1,1 Следующее проигрышное положение для начинающего игру 0, 2, 2 Все остальные положения 0, 2, С (где с = 3) выигрышны для начинающего Своим первым ходом он берет с-2 спички, оставляя противнику заведомо проигрышную позицию 0, 2, 2 " width="640"

Все остальные положения 0, 1, С (где с =2 ) выигрышны для начинающего

Своим первым ходом он берет с-1 спичку из третьей кучки, оставляя противнику заведомо проигрышную позицию 0,1,1

Следующее проигрышное положение для начинающего игру 0, 2, 2

Все остальные положения 0, 2, С (где с = 3) выигрышны для начинающего

Своим первым ходом он берет с-2 спички, оставляя противнику заведомо проигрышную позицию 0, 2, 2

Следующие проигрышные положения для начинающего игру 1, 2, 3 и 0, 3, 3

Здесь после каждого хода начинающего противник либо сразу выигрывает, либо сводит игру к позициям 0, 1, 1 или 0, 2, 2

0, 0, 0

0, 1, 1

1, 1, 1

0, 0, 1

0, 0, 2

2, 2, 2

0, 2, 2

1, 1, 2

1, 2, 2

0, 1, 2

0, 1, 3

0, 3, 3

0, 2, 3

1, 2, 3

0, 0, 3

1, 1, 3

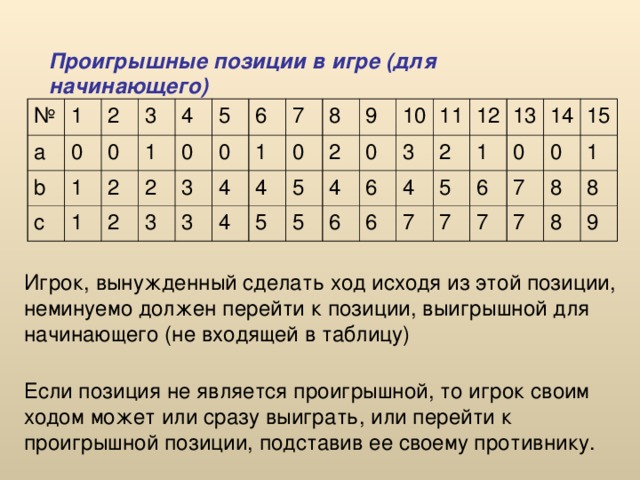
Проигрышные позиции в игре (для начинающего)

№

а

1

2

b

0

c

0

1

3

1

2

1

4

2

5

0

2

3

6

3

0

4

7

1

3

4

0

8

4

5

9

5

2

0

4

5

10

6

6

11

3

6

4

12

2

1

13

7

5

0

6

14

7

7

15

0

7

1

8

7

8

8

9

Игрок, вынужденный сделать ход исходя из этой позиции, неминуемо должен перейти к позиции, выигрышной для начинающего (не входящей в таблицу)

Если позиция не является проигрышной, то игрок своим ходом может или сразу выиграть, или перейти к проигрышной позиции, подставив ее своему противнику.

Игра ЦЗЯНЬШИЦЗЫ . На столе лежит 2 кучки спичек. Двое играющих поочередно берут спички из этих кучек, причем за один ход играющий может взять любое число спичек из одной кучки или поровну спичек из обеих куч. Выигравшим считается тот, кто возьмет последнюю спичку.

Задача : определить, при каких начальных положениях начинающий может выиграть, а при каких нет, и указать метод правильной (беспроигрышной) игры.

Пусть в наших 2-х кучках лежат соответственно а и b спичек, причем a

Положение, проигрышное для начинающего: 1, 2.

Возможные ходы: 1 спичка из 1-й кучки; 1 спичка из 2-й кучки; 2 спички из 2-й кучки; по 1-й спичке из каждой кучки. В любом случае противник следующим ходом заканчивает игру – выигрывает.

Все остальные положения, где одно из чисел равно 1 или 2 , или a – b = 1 , выигрышны для начинающего. Игру можно свести к положению 1, 2 – оно проигрышное, для противника.

Следующая проигрышная позиция 3, 5 : после каждого хода начинающего противник или сразу выигрывает, или сводит игру к позиции 1, 2. Все остальные позиции, где одно из чисел равно 3 или 5 , или a – b = 2 выигрышны для начинающего. Следующая проигрышная позиция 4, 7…

Проигрышная для начинающего в ЦЗЯНЬШИЦЗЫ

№

а

1

2

b

1

3

2

3

4

4

5

5

6

7

10

6

8

7

13

9

8

15

11

12

9

18

20

10

14

11

23

16

12

17

26

28

19

13

14

31

21

15

34

22

24

35

39

№

1

а

b

2

0

01

3

c

0

01

4

01

10

5

10

10

0

6

0

11

11

01

7

100

11

100

100

8

0

9

101

101

10

10

101

0

100

11

11

110

110

10

12

100

110

101

13

111

01

111

14

0

110

15

111

0

111

1000

111

01

1000

1000

1001

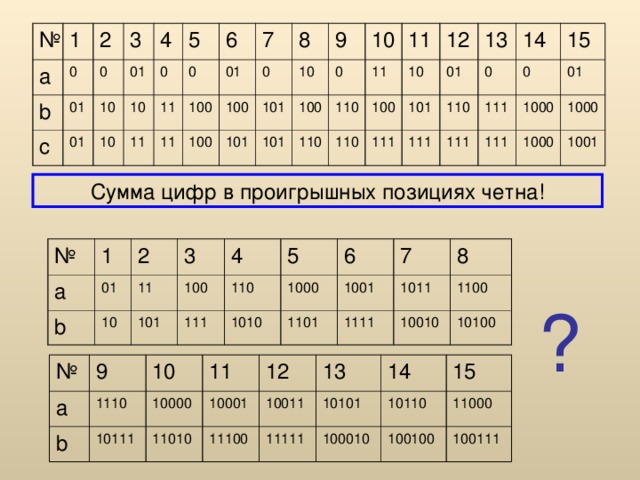
Сумма цифр в проигрышных позициях четна!

№

а

1

b

01

2

11

3

10

4

101

100

111

110

5

1010

6

1000

1001

7

1101

1011

8

1111

1100

10010

10100

?

№

а

9

b

10

1110

11

10000

10111

12

10001

11010

13

10011

11100

11111

14

10101

15

100010

10110

100100

11000

100111

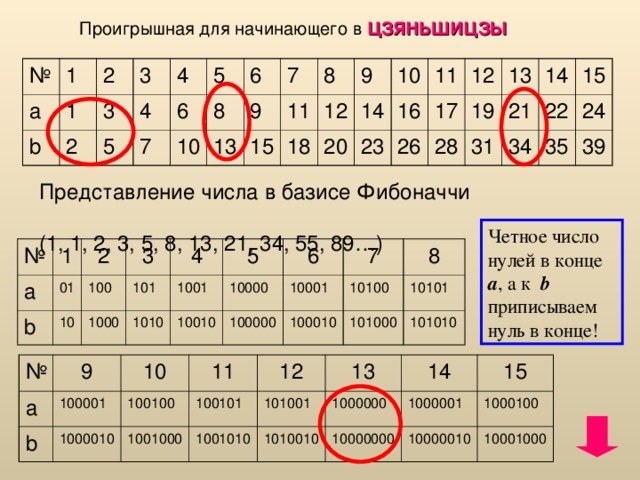
Проигрышная для начинающего в ЦЗЯНЬШИЦЗЫ

№

1

а

b

1

2

2

3

3

5

4

4

7

5

6

8

10

6

13

9

7

15

8

11

9

12

18

14

20

10

23

16

11

26

17

12

28

13

19

31

21

14

22

34

15

24

35

39

Представление числа в базисе Фибоначчи (1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…)

Четное число нулей в конце a , а к b приписываем нуль в конце!

№

а

1

b

2

01

10

100

3

4

1000

101

1010

1001

5

10010

10000

6

100000

10001

7

8

100010

10100

101000

10101

101010

№

а

9

b

10

100001

11

1000010

100100

12

1001000

100101

101001

1001010

13

14

1010010

1000000

15

1000001

10000000

1000100

10000010

10001000

К нетрадиционным системам счисления относится фибоначчиева система счисления . Базисом фибоначчиевой системы счисления является последовательность 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ..., т.е. подряд идущие числа Фибоначчи . В качестве цифр в этой системе счисления используются только цифры 0 и 1 .

Примеры :

37 10 = 34 + 3 = 1*34 + 21*0 + 13*0 + 8*0 + 5*0 + 3*1 +2*0 + 1*0 =100000100 Ф          

25 10 =21+3+1=1000101 Ф    

34 10 =34 =10000000 Ф   (7 цифр отсутствуют)

k 2 … kr 0. Здесь i j означает, что i = j +2. Целое неотрицательное число можно записать в виде последовательности нулей и единиц: N =( b m b m -1 … b 2 ) F , где b i = 1, если F i входит в преставление, иначе 0. Например, 1000000 = 832040 + 121393 + 46368 + 144 + 55 = F 30 + F 26 + F 24 + F 12 + F 10 или (1000000) 10 =(10001010000000000010100000000) F . Эта система счисления напоминает двоичное представление, за исключением того, что в ней никогда не встречаются две 1 подряд. " width="640"

Фибоначчиева система счисления (ФСС) основана на теореме Цеккендорфа , утверждающей, что любое целое положительное число имеет единственное представление вида N = F k 1 + F k 2 +…+ F kr ,

где F ki – число Фибоначчи, а k 1 k 2 … kr 0.

Здесь i j означает, что i = j +2. Целое неотрицательное число можно записать в виде последовательности нулей и единиц:

N =( b m b m -1 … b 2 ) F , где b i = 1, если F i входит в преставление, иначе 0.

Например, 1000000 = 832040 + 121393 + 46368 + 144 + 55 = F 30 + F 26 + F 24 + F 12 + F 10 или (1000000) 10 =(10001010000000000010100000000) F . Эта система счисления напоминает двоичное представление, за исключением того, что в ней никогда не встречаются две 1 подряд.

Теорема 1.

Проигрышными в игре НИМ являются те и только те позиции, для которых суммы всех цифр, отвечающих одному разряду в записи чисел a, b, c в двоичной системе счисления, для всех разрядов четны.

Теорема 2.

Проигрышными в игре ЦЗЯНЬШИЦЗЫ являются те и только те позиции ( a и b) , для которых число a , будучи записанным в фибоначчиевой системе счисления, кончается четным числом нулей, а число b получается приписыванием еще одного нуля в конце

Упражнения .

• Докажите, что если позиция ( a, b, c ) в игре НИМ не является проигрышной, т.е. не удовлетворяет указанным в формулировке теоремы 1 условиям, то играющий своим ходом может сделать ее проигрышной.
• Докажите, что если позиция ( a, b, c ) в игре НИМ является проигрышной, то после любого хода игрока она перестает быть таковой.
• Опишите проигрышные позиции ( a, b, c ) в игре НИМ, записывая числа не в двоичной, а в четверичной системе счисления.
• Докажите, что если позиция ( a, b ) в игре ( a, b, c ) в игре ЦЗЯНЬШИЦЗЫ не удовлетворяет условиям теоремы 2, то играющий может своим ходом либо сразу выиграть, либо свести позицию к проигрышной.