План урока № 53
Дисциплина: Геометрия
Тема: Пирамида, объем тела
Класс: 9 б
Дата проведения:_________
Цель урока: Формирование начальных сведений по теме «Пирамида»
-закрепить понятие пирамиды, ее элементов в ходе решения задач;
-рассмотреть применение пирамид на практике;
-обобщить и систематизировать знания учащихся по наиболее важным вопросам, связанным с решением геометрических задач; актуализация опорных знаний в условиях сдачи ОГЭ;
-развитие умений применять полученные знания на практике;
-формировать у учащихся творческий интерес при решении задач;
- развитие пространственного воображения, логического мышления.
Тип урока: комбинированный
Оборудование: ПК, проектор, учебник, раздаточный материал
План урока:
Организационный момент
Актуализация учебной деятельности учащихся
Применение полученных знаний в новых практических ситуациях
Подведение итогов урока
Домашнее задание
Ход урока
Организационный момент
а) сформулировать цели урока
Актуализация учебной деятельности учащихся
1) фронтальный опрос учащихся:
- объясните, что такое параллелепипед? Какие многоугольники являются гранями?
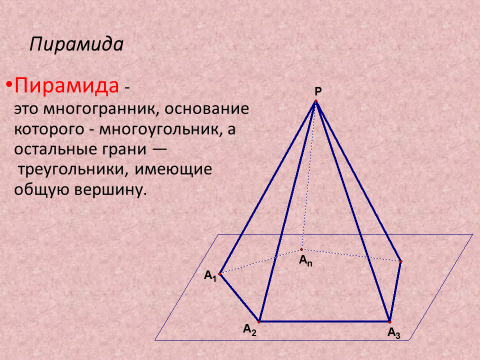
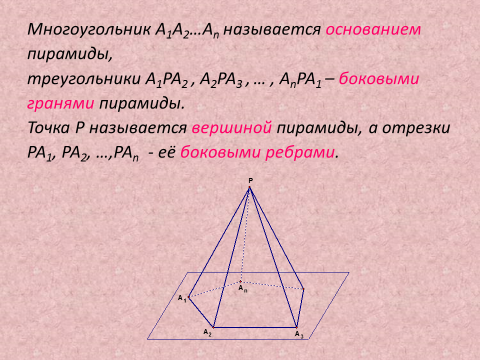
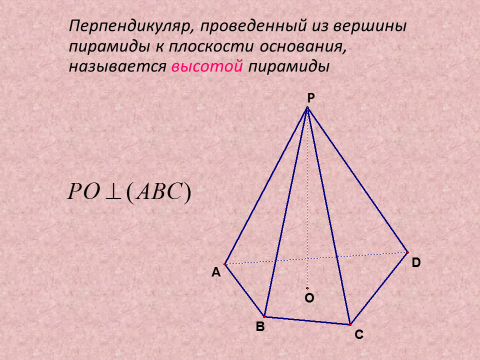
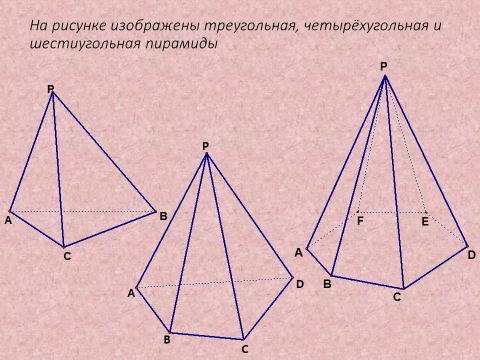
2) Рассмотреть Пирамида
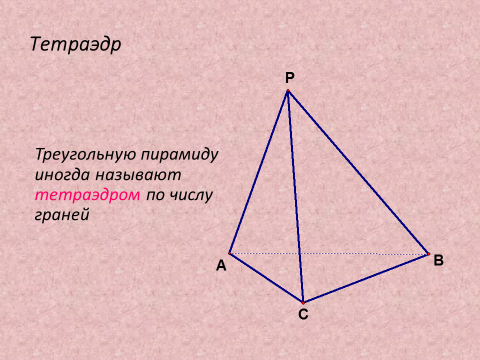
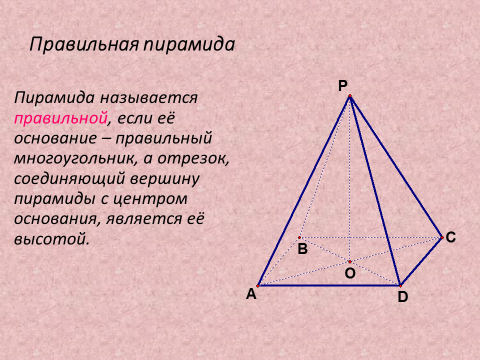
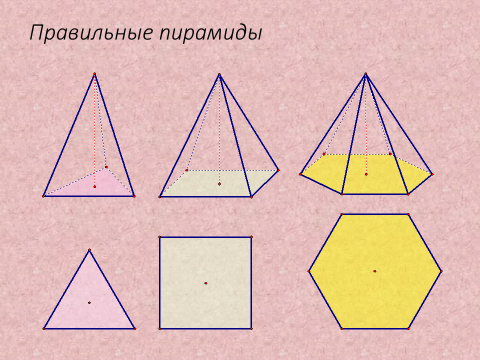
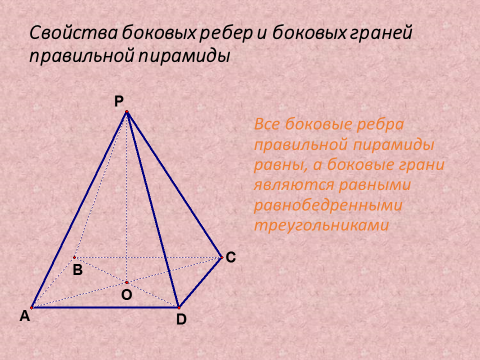
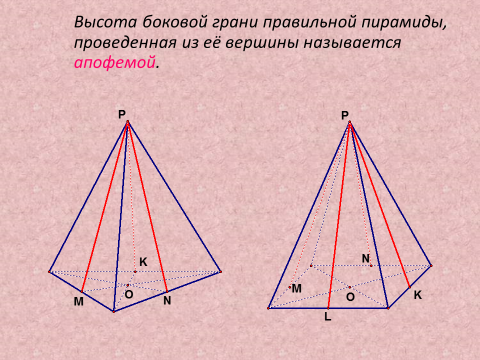

Применение полученных знаний в новых практических ситуациях
Решить задачу №1106
Докажем, что
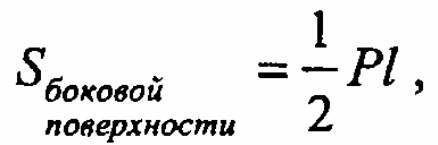

![]()
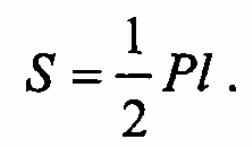

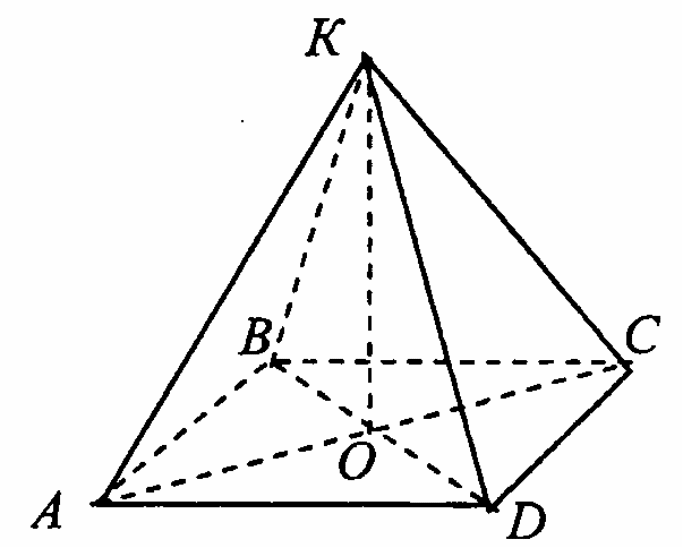

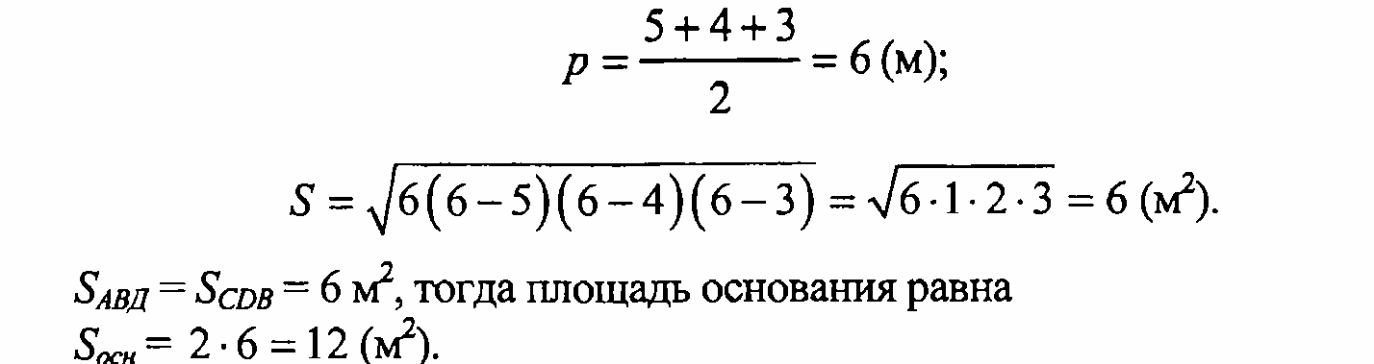
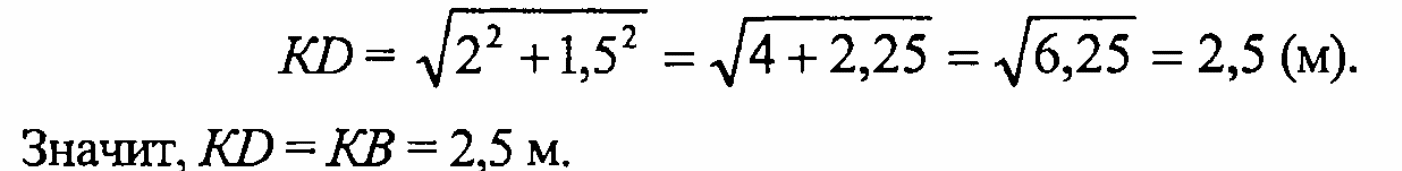

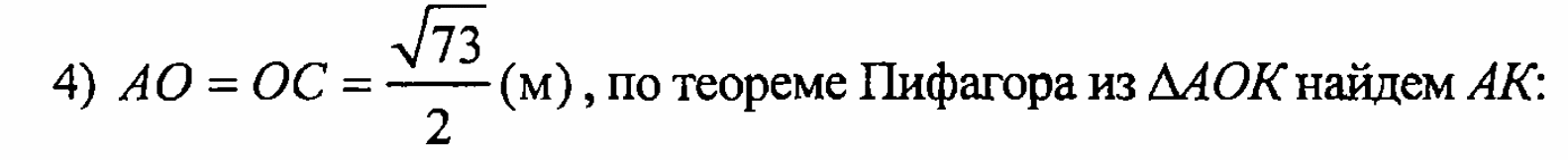
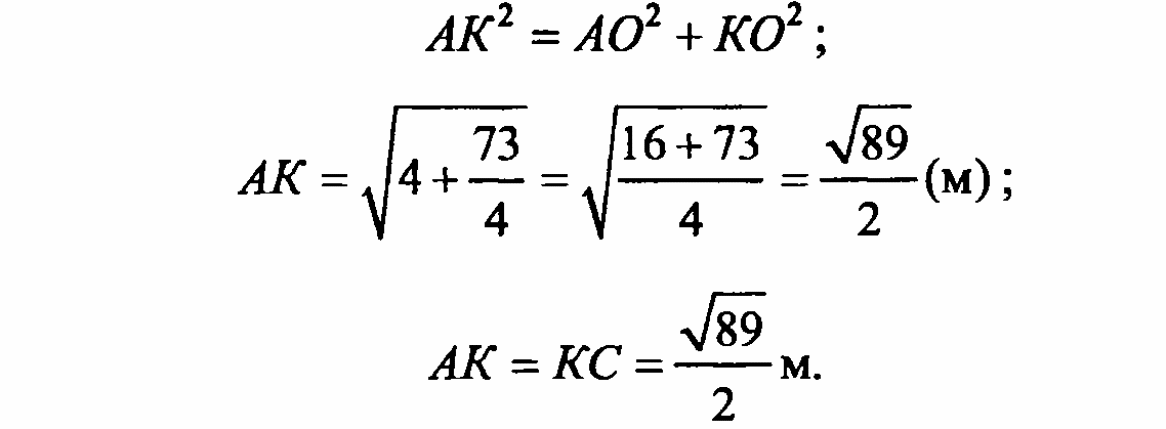
5)

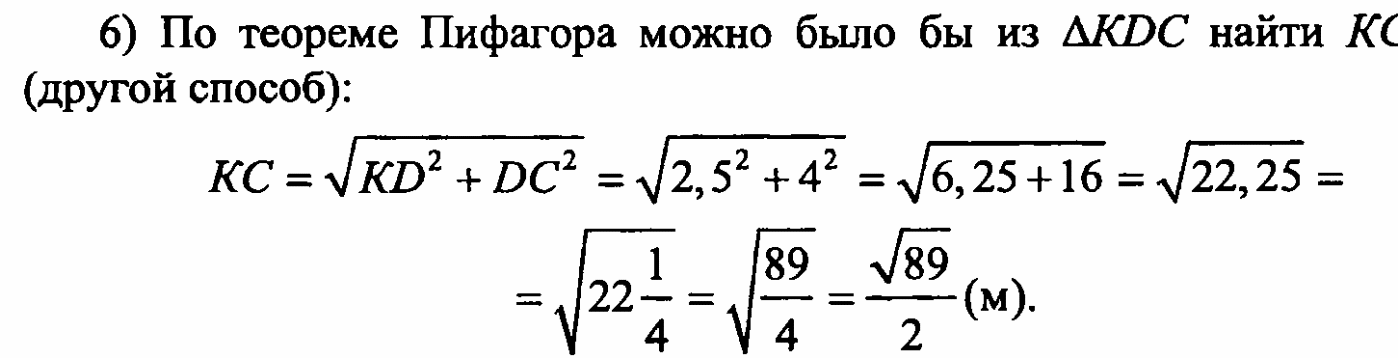
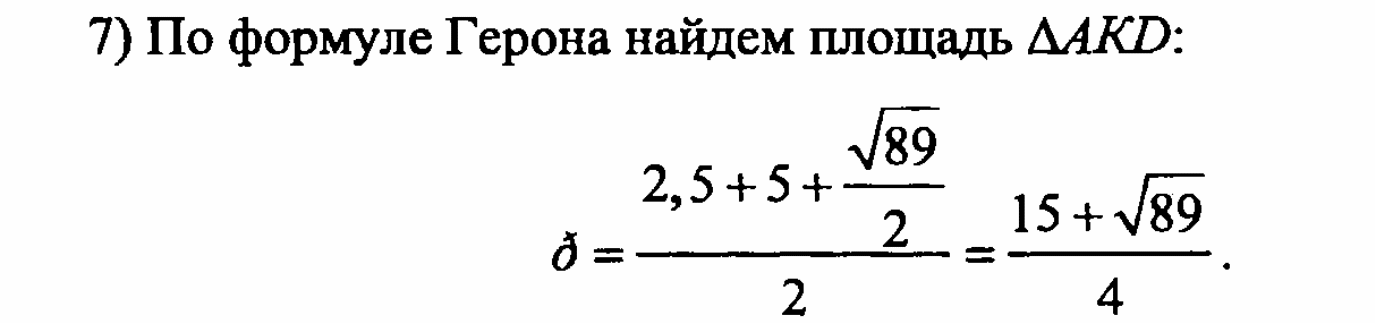
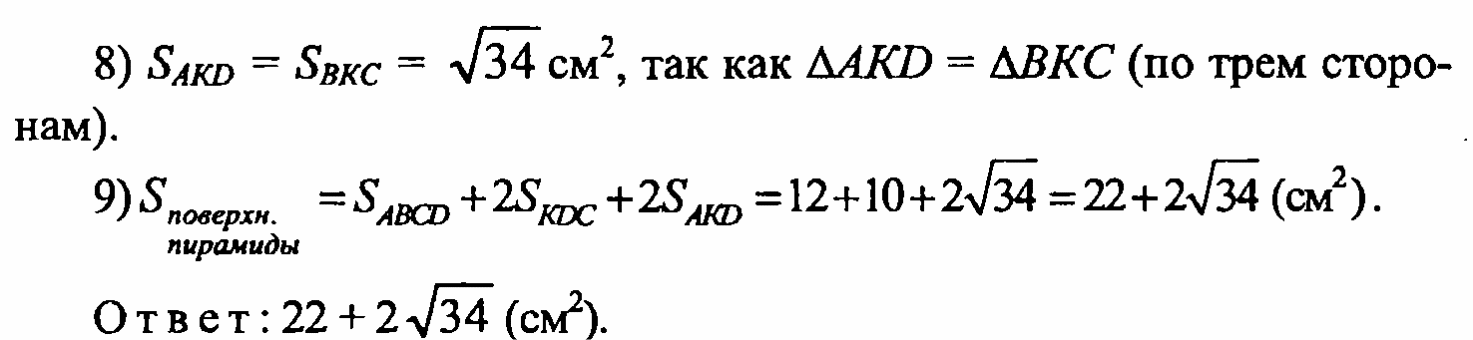
Задача №1242

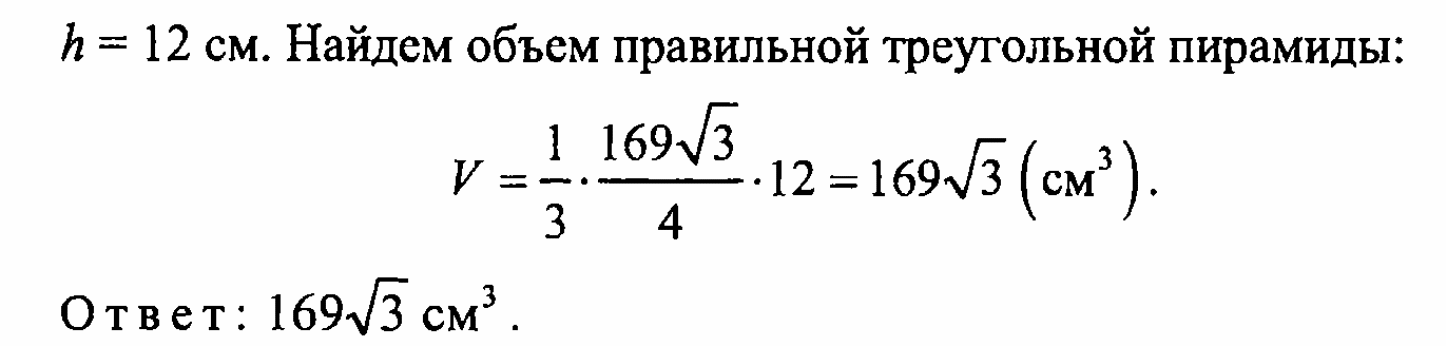
Подготовка к ОГЭ: решение задач модуля «Геометрия»
Подведение итогов урока
Домашнее задание
§1, п.118-121, №1203,1242, 1234 – задача на построение
Подготовка к ОГЭ – модуль «Геометрия»
16. Задание 16 № 351187
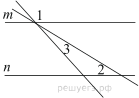
Прямые m и n параллельны. Найдите ∠3, если ∠1 = 129°, ∠2 = 1°. Ответ дайте в градусах.
Решение.
Введём обозначение как показано на рисунке. Углы 1 и 4 соответственные, поэтому ∠4 = ∠1 = 129°. Углы 2, 3 и 4 — это углы одного треугольника, сумма углов треугольника равна 180°, откуда ∠3 = 180° − 129° − 1° = 50°.
Ответ: 50.
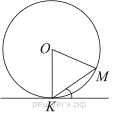
Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 32°. Найдите величину угла OMK. Ответ дайте в градусах.
Решение.
Угол, образованный хордой и касательной равен половине дуги, которую он заключает, поэтому величина дуги MK равна 2 · 32° = 64°. Угол MOK — центральный, поэтому он равен величине дуги, на которую опирается. Значит, угол MOK равен 64°. В треугольнике OMK стороны OK и OM равны как радиусы окружности, поэтому треугольник OMK — равнобедренный, следовательно, углы при основании равны. Сумма углов треугольника равна 180°, поэтому ∠OKM = ∠OMK = (180° − ∠KOM)/2 = (180° − 64°)/2 = 58°.
Ответ: 58.
18. Задание 18 № 340408
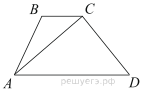
В трапеции ABCD AD = 3, BC = 1, а её площадь равна 12. Найдите площадь треугольника ABC.
Решение.
Пусть длина высоты трапеции равна ![]() Площадь трапеции можно найти как произведение полусуммы оснований на высоту:
Площадь трапеции можно найти как произведение полусуммы оснований на высоту:
![]()
Высота трапеции также является высотой треугольника ![]() Найдём площадь треугольника
Найдём площадь треугольника ![]() как полупроизведение основания на высоту:
как полупроизведение основания на высоту:
![]()
Ответ: 3.
19. Задание 19 № 350608
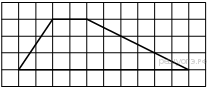 На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.
Решение.
Длина средней линии трапеции равна полусумме её оснований, т.е. ![]()
Ответ: 6.
20. Задание 20 № 314884
Какие из данных утверждений верны? Запишите их номера.
1) Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности.
2) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны, то эти прямые параллельны.
3) У равнобедренного треугольника есть центр симметрии.
Ответ: 2.
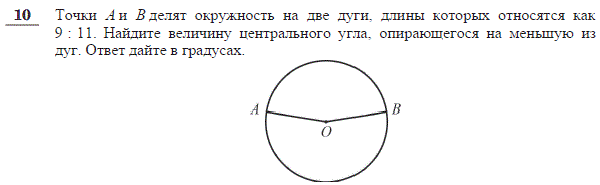
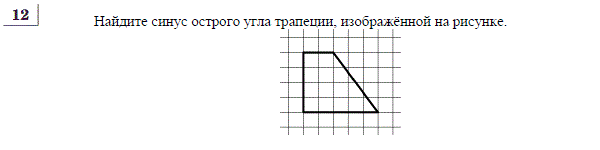
Вариант - 1

Вариант -2

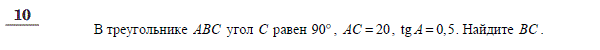


 Получите свидетельство
Получите свидетельство Вход
Вход











 Длина окружности и площадь круга. (2.28 MB)
Длина окружности и площадь круга. (2.28 MB)
 0
0 261
261 1
1 Нравится
0
Нравится
0


