Длина окружности

Представим. Что мы разрезаем окружность и «распрямляем» ее в нить.

Длина получившегося в этом случае отрезка и есть длина окружности.

Длина окружности обозначается буквой C.

Число π, обозначающее отношение длины окружности к её диаметру, заинтересовало людей ещё в древние времена. Уже в Египте времён фараонов и в Индии VI века до н.э. это отношение оценивалось как 3,16. Более точное значение числа π и алгоритм его вычисления предложил в III в до н.э. Архимед.

В первой половине XV в. обсерватории Улугбека, возле Самарканда, астроном и математик ал-Каши вычислил "пи" с 16 десятичными знаками. Он сделал 27 удвоений числа сторон многоугольников и дошёл до многоугольника, имеющего 3*228 углов. Ал-Каши произвёл уникальные расчёты, которые были нужны для составления таблицы синусов с шагом в 1'. Эти таблицы сыграли важную роль в астрономии.

Только через 250 лет после ал-Каши его результат был превзойдён.

МБОУ Видновская СОШ №9 Учитель математики Кудимова Антонина Васильевна 2013г

Длина окружности

Вдохновение

нужно в геометрии,

как и в поэзии…

А.С. Пушкин

Окружность вокруг нас

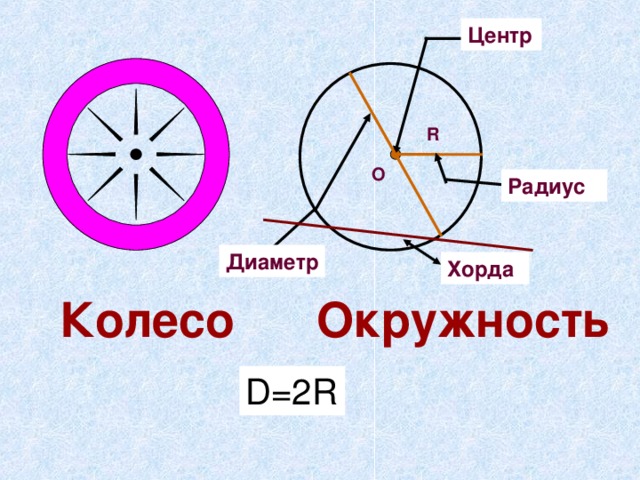
Центр

R

О

Радиус

Диаметр

Хорда

Окружность

Колесо

D=2R

Представим. Что мы разрезаем окружность и «распрямляем» ее в нить.

Длина получившегося в этом случае отрезка и есть длина окружности.

Представим. Что мы разрезаем окружность и «распрямляем» ее в нить.

Длина получившегося в этом случае отрезка и есть длина окружности.

Длина окружности обозначается буквой C .

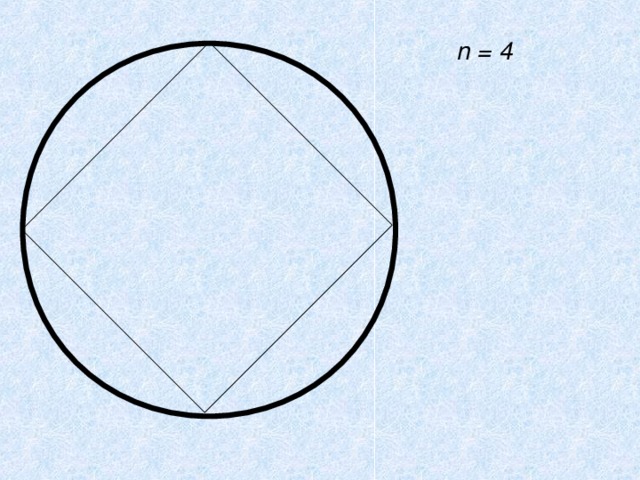
n = 4

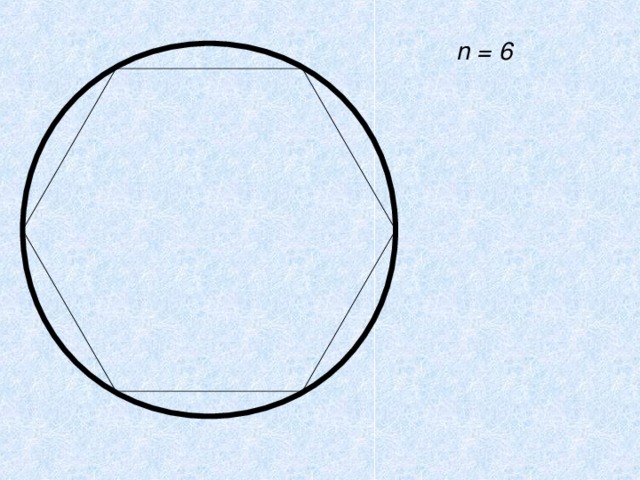
n = 6

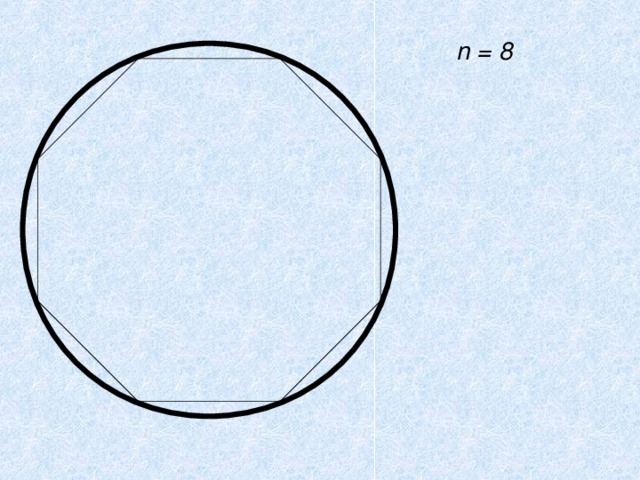
n = 8

С= 2 R или С= D

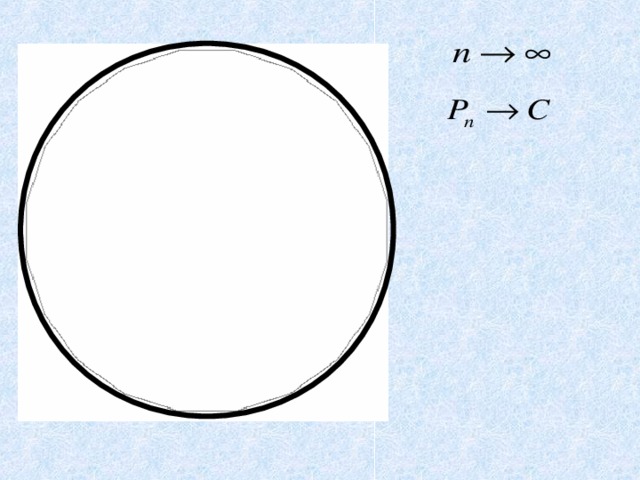
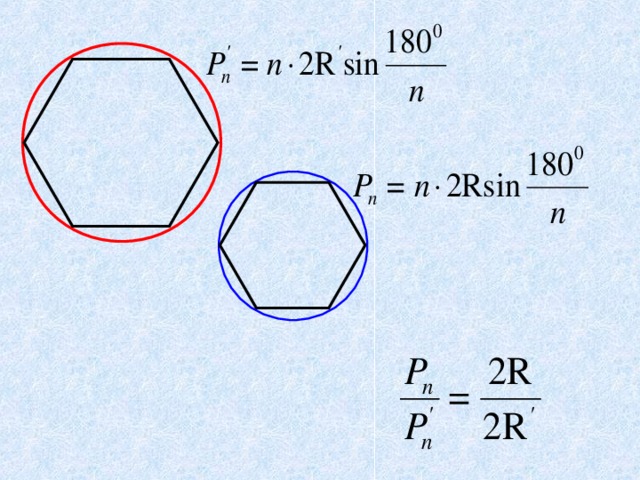
• С= 2 R или С= D

Число (пи) ‏

• Число π, обозначающее отношение длины окружности к её диаметру, заинтересовало людей ещё в древние времена. Уже в Египте времён фараонов и в Индии VI века до н.э. это отношение оценивалось как 3,16. Более точное значение числа π и алгоритм его вычисления предложил в III в до н.э. Архимед

В первой половине XV в. обсерватории Улугбека , возле Самарканда , астроном и математик ал-Каши вычислил "пи" с 16 десятичными знаками. Он сделал 27 удвоений числа сторон многоугольников и дошёл до многоугольника, имеющего 3*2 28 углов. Ал-Каши произвёл уникальные расчёты, которые были нужны для составления таблицы синусов с шагом в 1' . Эти таблицы сыграли важную роль в астрономии.

Только через 250 лет после ал-Каши его результат был превзойдён.

Первым ввёл обозначение отношения длины окружности к диаметру современным символом

английский математик У.Джонсон в 1706 г. В качестве символа он взял первую букву греческого слова "periferia" , что в переводе означает "окружность" .

Гордый Рим трубил победу Над твердыней Сиракуз; Но трудами Архимеда Много больше я горжусь. Надо нынче нам заняться, Оказать старинке честь, Чтобы нам не ошибаться, Чтоб окружность верно счесть, Надо только постараться И запомнить все как есть Три — четырнадцать — пятнадцать — девяносто два и шесть!..

Точное значение неизвестно и сейчас

• Число встречается во множестве формул геометрии, математического анализа, теории чисел, динамики, физики, теории вероятности и математической статистики. В IT-индустрии, вычисления числа используются при тестировании суперкомпьютеров. В Токийском университете в 2002 году число было определено до 1,241,100,000,000-го знака на 64-х ядерном Hitachi с терабайтом оперативной памяти и производительностью 2 триллиона операций в секунду.

= 3, 1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989…

Какое бы сочетание цифр мы бы ни выдумали — оно непременно встретится в знаках числа , то есть можно ожидать появление любой наперед заданной последовательности цифр

= 3, 1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989…

Есть гипотезы, предполагающие, что в числе пи скрыта любая информация, которая когда-либо была или будет доступна людям.

Интересные факты

Отношение длины основания Великой Пирамиды к ее высоте, разделенное пополам, дает знаменитое число "пи" .

Возможно, оно намеренно зашифровано в размерах Пирамиды Хеопса, причем с более точным значением, чем его знал великий Архимед, живший позже на 2000 лет!

Интересные факты

Лидером по тупым законам по праву может считаться Американский штат Индиана. Там на ряду с законами запрещающими носить усы людям часто прибегающим к поцелуям, продавать молоко в винных магазинах и перекрашивать в другой цвет птиц и животных, действует закон о том, что на территории штата число  . следует считать равным 4

где - градусная мера угла

где - радианная мера угла

R=2,5 см

R=2 см

Задача № 1:

Определите длины внутренней и внешней окружностей колеса, если изображение сделано в масштабе 1:20

( )

Решение

Задача № 2:

Радиус закругления железнодорожного полотна равен 5 км, а длина дуги закругления — 400 м. Какова градусная мера дуги закругления?

Тест

Вариант I

D - ?

1. C = 0,785 м

a) 0,25; б) 2,5; в) 25

2. С = 54,95 см

а) 175; б) 0,175; в) 17,5

Вариант II

D - ?

1. C = 0,2669 cм

а) 8,5; б) 0,85; в) 0,085

2. С = 4,71 м

а) 15; б) 1,5; в) 0,15

• Вариант II D - ? 1. C = 0,2669 cм а) 8,5; б) 0,85; в) 0,085 2. С = 4,71 м а) 15; б) 1,5; в) 0,15

Тест

Вариант I

D - ?

1. C = 0,785 м

a) 0,25; б) 2,5; в) 25

2. С = 54,95 см

а) 175; б) 0,175; в) 17,5

1. а) ‏

2. в) ‏

Вариант II

D - ?

1. C = 0,2669 cм

а) 8,5; б) 0,85; в) 0,085

2. С = 4,71 м

а) 15; б) 1,5; в) 0,15

1. в) ‏

2. б) ‏

• Вариант II D - ? 1. C = 0,2669 cм а) 8,5; б) 0,85; в) 0,085 2. С = 4,71 м а) 15; б) 1,5; в) 0,15 1. в) ‏ 2. б) ‏

Итоги урока

1. Какая формула используется для вычисления длины окружности?

2. Что означает число и чему равно его приближенное значение?

3. По какой формуле вычисляется длина дуги окружности?

Домашнее задание

§ 2, п.110, ответить на вопросы 8-10, стр. 290, № 1112.

Решить задачу: Диаметр основания Царь-колокола, находящегося в Московском кремле, равен 6,6 м. Найдите длину основания колокола.

По желанию: Вычислить длину экватора Земли, если радиус Земли равен 6370 км.