Начнём с примера.
Под действием воздушных масс воздушный шар сначала двигался из точки А в точку B, а затем из точки B переместился в точку C.
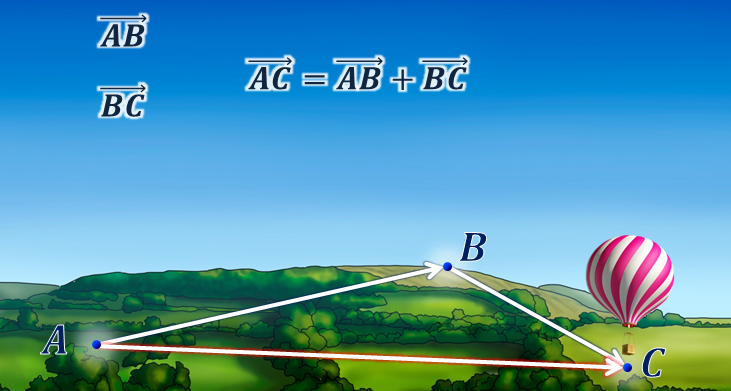
Каждое
из этих двух перемещений можно представить в виде вектора 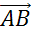 и
и 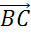 .
.
Но
можно ведь сказать, что в результате воздушный шар из точки А попал в точку C.
И это перемещение задает вектор 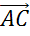 .
.
Так
как перемещение из точки А в C
складывается из перемещений из точки А в B
и из B в C,
то можно записать, что вектор 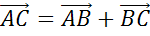 .
.
Этот пример подводит нас к понятию суммы двух векторов.
Рассмотрим
два ненулевых вектора: 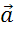 и
и
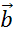 .
.
Отметим
произвольную точку А и отложим от неё вектор 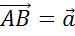 . Далее от точки B
отложим вектор
. Далее от точки B
отложим вектор 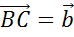 .
.
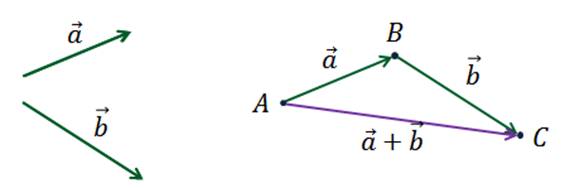
Можем
изобразить вектор 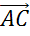 ,
который называется суммой векторов
,
который называется суммой векторов 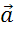 и
и 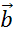 . Сумму векторов
обозначают так
. Сумму векторов
обозначают так 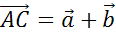 .
.
Данное правило сложения векторов будем называть правилом треугольника.
Вы могли усомниться, что точку А, действительно, можно выбирать произвольно.
Докажем это.
Найдём
сумму векторов 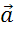 и
и
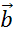 , но начнём откладывать
их от некоторой точки А1.
, но начнём откладывать
их от некоторой точки А1.
Нам необходимо доказать,
что полученный вектор 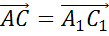 .
.
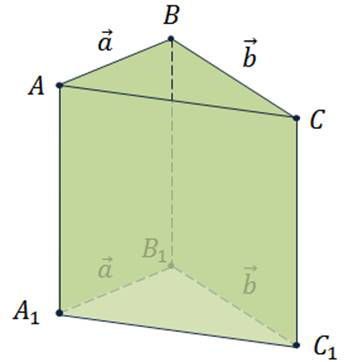
Из построений очевидно,
что векторы 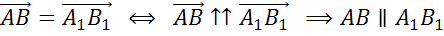
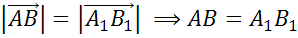 ,
, 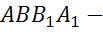 параллелограмм
параллелограмм
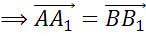
Аналогично, из равенства
векторов 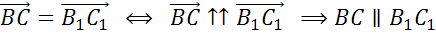
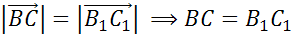 ,
, 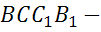 параллелограмм
параллелограмм
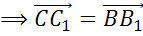
Из полученных равенств
получаем, что равны 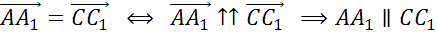 ,
,
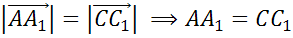
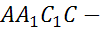 параллелограмм
параллелограмм
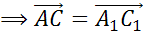 .
.
Что и требовалось доказать.
Изобразить вектор суммы двух векторов:

Решение.

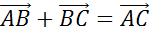 ,
, 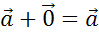
А также, опираясь на
пункты 1 и 2, правило треугольника можно сформулировать так. Сумма векторов 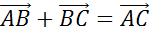 . Где А, B
и C — произвольные точки.
. Где А, B
и C — произвольные точки.
Для троек произвольных точек продолжим равенства.
Для
точек К, L и М сумма векторов 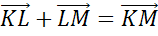 .
.
Для
точек X, Y
и Z сумма векторов 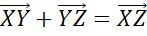 .
.
Для
последней тройки точек R,
S и Т сумма векторов 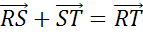 .
.
Выполним несколько заданий.
Задача.
Начертить
попарно неколлинеарные векторы 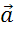 ,
, 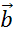 и
и 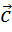 .
.
Построить:
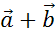 ,
, 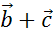 ,
, 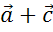 .
.

Решение.

Задача. Для каждого равенства, задающего сумму векторов,
указать соответствующий рисунок.
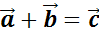 ,
, 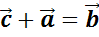 ,
, 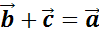
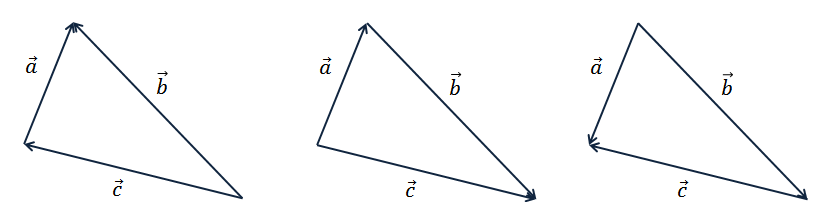
Решение.
Посмотрим на первый рисунок. Найдём вектор, начало которого совпадает с началом некоторого вектора, а конец — с концом некоторого вектора.
Таким
вектором является вектор 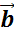 .
Значит, он будет являться суммой, а векторы
.
Значит, он будет являться суммой, а векторы 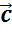 и
и 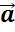 — соответственно
первым и вторым слагаемыми.
— соответственно
первым и вторым слагаемыми.
Посмотрим
на следующий рисунок. Рассуждая так же как в предыдущем пункте, делаем вывод,
что вектор 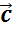 является
суммой, а векторы
является
суммой, а векторы 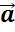 и
и
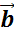 — соответственно
первым и вторым слагаемыми.
— соответственно
первым и вторым слагаемыми.
На
последнем рисунке вектора 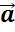 является
суммой, а векторы
является
суммой, а векторы 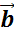 и
и
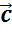 —
соответственно первым и вторым слагаемыми.
—
соответственно первым и вторым слагаемыми.
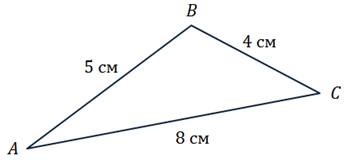
Задача.
Стороны 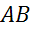 ,
,
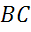 и
и 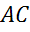 треугольника
соответственно равны
треугольника
соответственно равны 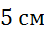 ,
,
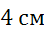 и
и 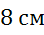 .Найти длины векторов:
.Найти длины векторов: 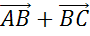 ,
, 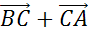 ,
, 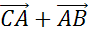 .
.
Решение.
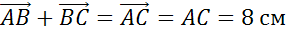
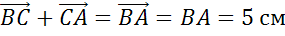
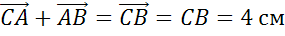
Ответ:
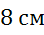 ,
, 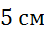 ,
, 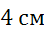 .
.
Подведём итоги нашего урока.
Сегодня мы познакомились с правилом треугольника сложения векторов.
Для
того, чтобы изобразить вектор суммы двух векторов 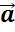 и
и 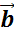 , от некоторой точки А
откладывают вектор
, от некоторой точки А
откладывают вектор 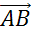 ,
равный вектору
,
равный вектору 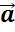 .
Далее от точки B откладывают
вектор
.
Далее от точки B откладывают
вектор 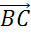 ,
равный вектору
,
равный вектору 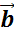 .
Тогда вектор
.
Тогда вектор 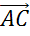 является
вектором суммы двух векторов
является
вектором суммы двух векторов 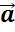 и
и
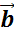 .
.
Исходя
из данных построений, правило треугольника можно записать в виде такой
формулы 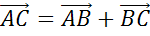 ,
где А, B и C
— произвольные точки.
,
где А, B и C
— произвольные точки.
Складывая
по правилу треугольника произвольный вектор 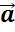 с нулевым вектором,
получаем, что их сумма равна вектору
с нулевым вектором,
получаем, что их сумма равна вектору 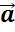 .
.

 Получите свидетельство
Получите свидетельство Вход
Вход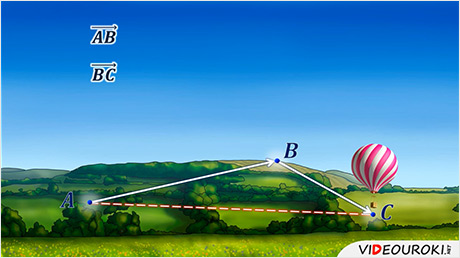



 0
0 8467
8467

