С прошлых уроков вам уже известно, что векторы можно складывать и делать это вы уже умеете с помощью правила треугольника.
Для
того, чтобы изобразить вектор суммы двух векторов 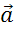 и
и
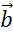 ,
от некоторой точки А откладывают вектор
,
от некоторой точки А откладывают вектор 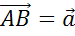 .
Далее от точки B откладывают
вектор
.
Далее от точки B откладывают
вектор 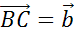 .
Тогда вектор
.
Тогда вектор 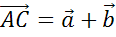 .
.
Для дальнейшей работы с векторами нам понадобится знание следующих законов сложения векторов.
Сумма
векторов 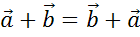 .
Этот закон называют переместительным законом: от перемены мест
слагаемых сумма не меняется.
.
Этот закон называют переместительным законом: от перемены мест
слагаемых сумма не меняется.
И
ещё один закон. 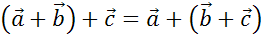 .
Этот закон называют сочетательным законом.
.
Этот закон называют сочетательным законом.
По очереди докажем каждый из них.
Рассмотрим
переместительный закон для неколлинеарных векторов 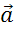 и
и
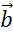 .
.
Доказательство.
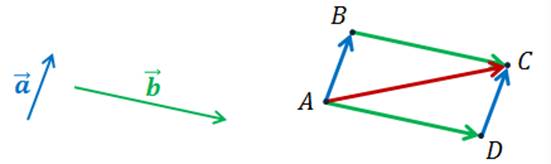
Итак,
от произвольной точки А отложим вектор 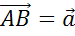 ,
и вектор
,
и вектор 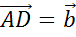 .
.
На этих векторах построим параллелограмм ABCD.
А
теперь, пользуясь правилом треугольника сложения двух векторов, заметим, что 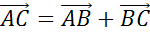 ,
то есть равен сумме векторов
,
то есть равен сумме векторов 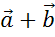 .
.
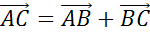 ,
,
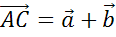
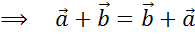
С
дугой стороны, 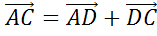 ,
,
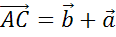
Отсюда
можем сделать вывод, что сумма векторов 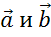 равна
сумме векторов
равна
сумме векторов 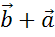 .
.
Что и требовалось доказать.
Теперь
перейдём к доказательству сочетательного закона для трёх неколлинеарных
векторов 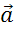 ,
,
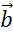 ,
,
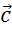 .
.
От
произвольной точки А отложим Вектор 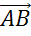 ,
равный вектору
,
равный вектору 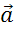 .
От точки B отложим вектор
.
От точки B отложим вектор 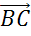 ,
равный вектору
,
равный вектору 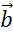 .
А от точки C отложим вектор
.
А от точки C отложим вектор 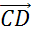 ,
равный вектору
,
равный вектору 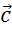 .
.
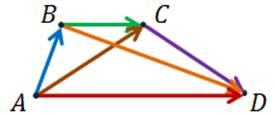
Рассмотрим
левую часть равенства, выражающего сочетательный закон. Запишем вектора 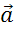 ,
,
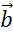 ,
,
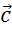 как
как
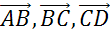 .
.
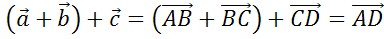
В
скобках записана сумма векторов 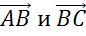 .
Пользуясь правилом треугольника, можем записать, что эта сумма равна вектору
.
Пользуясь правилом треугольника, можем записать, что эта сумма равна вектору 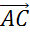 .
.
А
сумма вектора 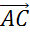 и
и
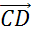 ,
в свою очередь, по правилу треугольника равна вектору
,
в свою очередь, по правилу треугольника равна вектору 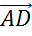 .
.
Теперь аналогично поступим с правой частью равенства, задающего сочетательный закон.
По
правилу треугольника 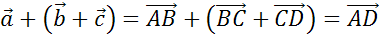 .
.
Отсюда
делаем вывод, 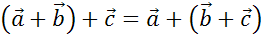 .
.
Что и требовалось доказать.
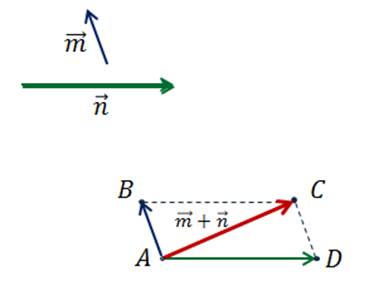
Вернёмся к рисунку из доказательства переместительного закона.
Обратите
внимание, если векторы 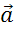 ,
,
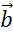 отложить
от одной точки и построить на них параллелограмм, то диагональ этого
параллелограмма задаёт вектор суммы векторов
отложить
от одной точки и построить на них параллелограмм, то диагональ этого
параллелограмма задаёт вектор суммы векторов 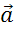 и
и
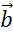 .
.
Такое правило сложения векторов называют правилом параллелограмма.
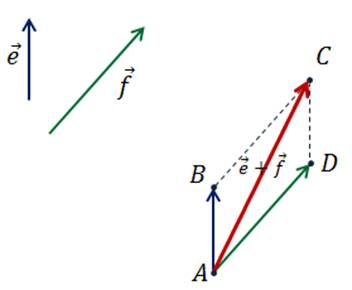
Изобразим вектор суммы для каждой пары векторов, пользуясь правилом параллелограмма.
Первым
изобразим вектор суммы векторов 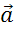 и
и
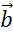 .
.
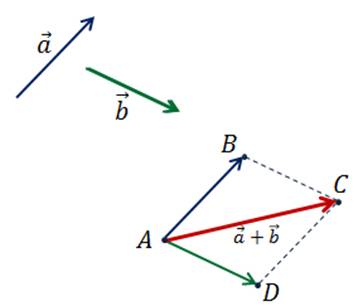
Отложим
от произвольной точки А вектор 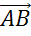 ,
равный вектору
,
равный вектору 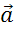 .
.
Далее
от точки А отложим вектор 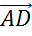 ,
равный вектору
,
равный вектору 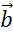 .
.
Теперь
на этих векторах построим параллелограмм ABCD.
Вектор 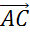 является
вектором суммы векторов
является
вектором суммы векторов 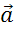 и
и
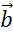 .
.
Далее
изобразим вектор суммы векторов 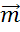 и
и
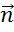 .
.
Обратите внимание, что каждый раз вектор суммы берёт своё начала из точки начала обоих векторов-слагаемых.
Последним изобразим
вектор суммы векторов 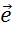 и
и
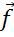 .
.
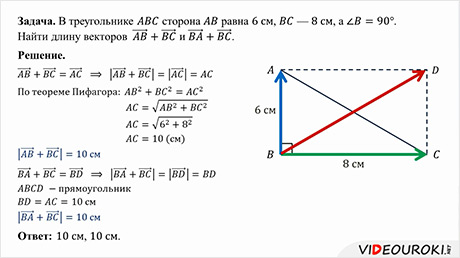
Задача.
В треугольнике 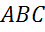 сторона
сторона
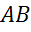 равна
равна
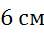 ,
,
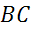 —
—
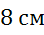 ,
а
,
а 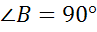 .
.
Найти
длину векторов 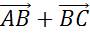 и
и
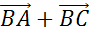 .
.
Решение.
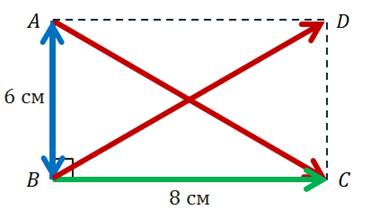
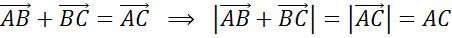
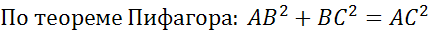
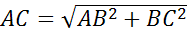
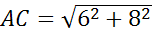
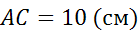
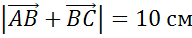
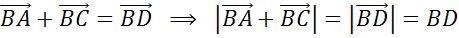
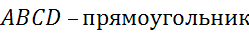
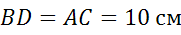
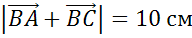
Ответ:
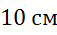 ,
,
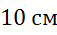 .
.
Давайте подведём итоги нашего урока.
Сегодня вы познакомились с законами сложения векторов. А именно с переместительным и сочетательным законами сложения векторов. А так же освоили правило параллелограмма для сложения двух векторов.
Оно заключается в следующем: чтобы сложить
неколлинеарные векторы 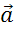 и
и
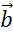 ,
нужно отложить от произвольной точки А векторы
,
нужно отложить от произвольной точки А векторы 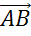 и
и
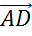 равные
векторам
равные
векторам 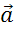 и
и
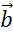 соответственно,
и построить на них параллелограмм ABCD.
Тогда вектор
соответственно,
и построить на них параллелограмм ABCD.
Тогда вектор
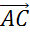 равен
сумме векторов
равен
сумме векторов 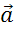 и
и
 .
.

 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 27448
27448

