Вам уже известны правила сложения двух векторов.
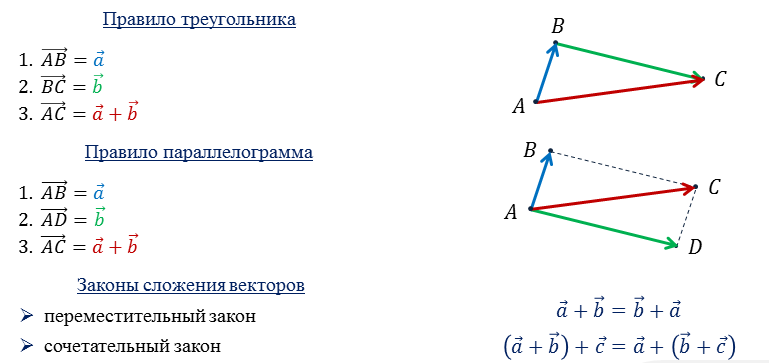
Cегодня мы будем учиться складывать несколько векторов.
Построим
вектор суммы векторов 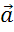 ,
, 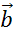 ,
, 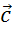 .
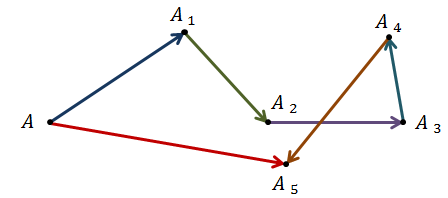
От некоторой точки А отложим вектор
.
От некоторой точки А отложим вектор
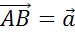 . Далее от точки B
отложим вектор
. Далее от точки B
отложим вектор 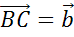 .
А от точки C отложим вектор
.
А от точки C отложим вектор
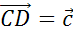 .
.
Будем последовательно складывать наши векторы, пользуясь правилом треугольника.
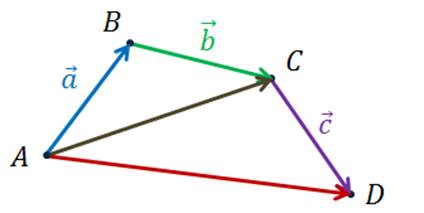
Сумма
векторов 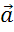 ,
, 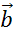 равна вектору
равна вектору 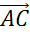 .
.
Теперь
к вектору 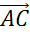 добавим
вектор
добавим
вектор 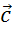 . В результате мы
получаем вектор
. В результате мы
получаем вектор 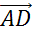 .
.
Тогда
можем сказать, что сумма 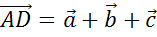 .
.
Так, последовательно складывая первый вектор со вторым, затем их сумму с третьим и так далее, можно найти суммы четырёх, пяти и большего числа векторов.
Такое правило построения суммы векторов называют правилом многоугольника.
Сформулируем его в общем виде.
Если А1, А2,
…, An — произвольные точки
плоскости, то сумма векторов 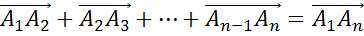
.
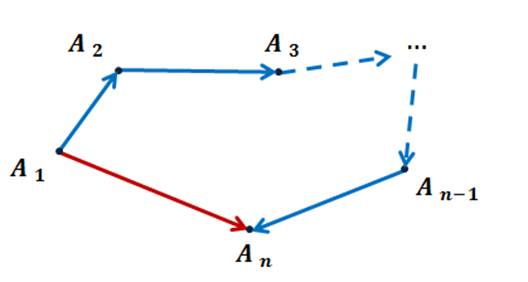
Это равенство справедливо для любых точек А1, А2, …, An. И, в частности, для случая, когда некоторые из них совпадают.
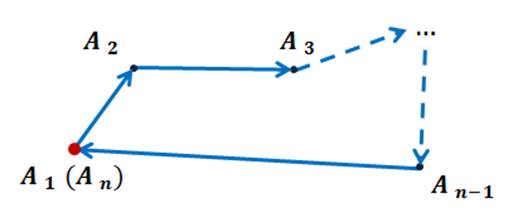
Например, если начало первого вектора совпадает с концом последнего, то сумма данных векторов равна нулевому вектору.
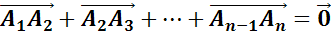
Задача.
Построить
вектор суммы попарно неколлинеарных векторов 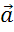 ,
, 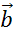 ,
, 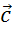 ,
, 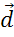 и
и 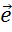 .
.
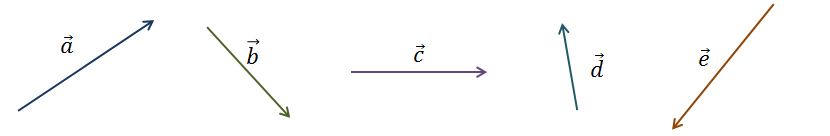
Построение
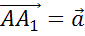
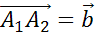
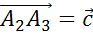
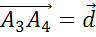
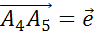
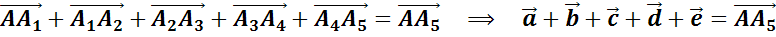 .
.
Задача. В соответствии с правилом многоугольника составить равенство,выражающее сумму нескольких векторов.
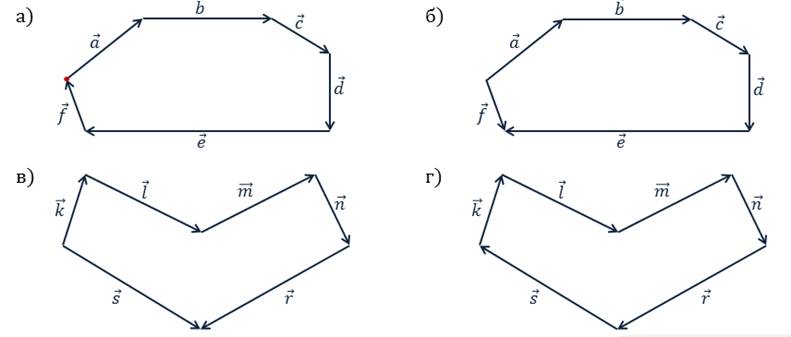
Посмотрим на первый рисунок. Мы
видим, что последовательно складывают векторы 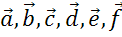 . Но, так как
начало вектора
. Но, так как
начало вектора 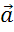 совпадает
с концом вектора
совпадает
с концом вектора 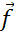 ,
то сумма данных векторов равна нулевому вектору
,
то сумма данных векторов равна нулевому вектору 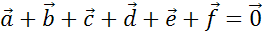 .
.
Перейдём к следующему случаю.
Видим, что сумма состоит
из векторов 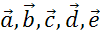 .
А вот вектор
.
А вот вектор 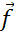 ,
как раз таки, и равен ей.
,
как раз таки, и равен ей.
На рисунке в
последовательно, друг за другом, отложены векторы 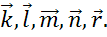 Ну, а вектор
Ну, а вектор
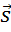 равен их
сумме.
равен их
сумме.
На последнем рисунке
последовательно, друг за другом, отложены векторы 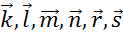 . При этом Начало
вектора К совпадает с концом вектора С. Поэтому сумма данных векторов равна
нулевому вектору
. При этом Начало
вектора К совпадает с концом вектора С. Поэтому сумма данных векторов равна
нулевому вектору 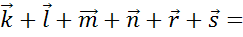
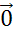 .
.
Задача. 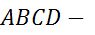 равнобокая
трапеция.
равнобокая
трапеция.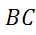 и
и
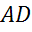 — её
основания, боковая сторона равна
— её
основания, боковая сторона равна 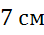 . Построить вектор
. Построить вектор
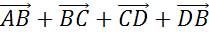 и найти его
длину.
и найти его
длину.
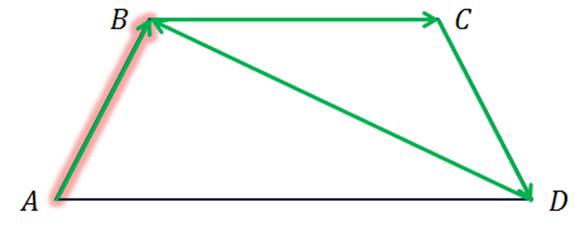
Построение
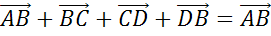
Решение.
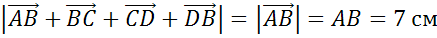
Ответ:
А теперь подведём итоги нашего урока.
Сегодня мы познакомились с правилом многоугольника, которое позволяет строить вектор суммы нескольких векторов.
Его суть заключается в том, что векторы-слагаемые последовательно откладывают друг от друга, суммой является вектор, начало которого совпадает с началом первого вектора-слагаемого, а конец совпадает с концом последнего вектора-слагаемого.
Если эти точки совпадают, то сумма данных векторов равна нулевому вектору.

 Получите свидетельство
Получите свидетельство Вход
Вход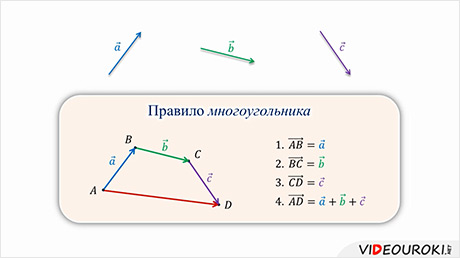



 0
0 18393
18393

