Вам уже знакомы правила сложения векторов.
Чтобы сложить
неколлинеарные векторы  и
и
 по правилу
треугольника, нужно от некоторой точки А отложить вектор
по правилу
треугольника, нужно от некоторой точки А отложить вектор 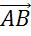 , равный вектору
, равный вектору  . Далее от точки B
отложить вектор
. Далее от точки B
отложить вектор 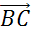 ,
равный вектору
,
равный вектору  .
Вектор
.
Вектор 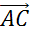 является
вектором суммы двух векторов
является
вектором суммы двух векторов  и
и
 .
.
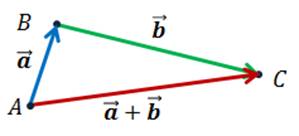
Для
сложения этих же векторов можно использовать правило параллелограмма. При этом
нужно отложить от произвольной точки А векторы 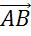 и
и 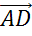 , равные векторам
, равные векторам  и
и
 соответственно, и
построить на них параллелограмм ABCD.
Тогда вектор
соответственно, и
построить на них параллелограмм ABCD.
Тогда вектор 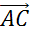 равен
сумме векторов
равен
сумме векторов  и
и
 .
.
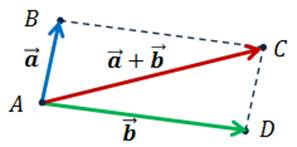
Для сложения нескольких векторов применяют правило многоугольника. При этом от некоторой точки последовательно откладывают векторы друг за другом, и вектором их суммы является вектор, проведённый от начала первого вектора к концу последнего.
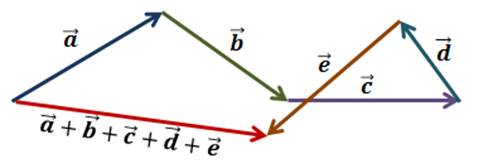
Так же вам известны законы сложения векторов: переместительный и сочетательный.
На
этом уроке поговорим о разности двух векторов. Её обозначают так 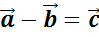 .
.
Разностью
векторов 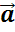 и
и
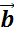 называют
такой вектор
называют
такой вектор 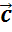 ,
сумма которого с вектором
,
сумма которого с вектором  равна
вектору
равна
вектору  .
.
Чтобы получить представление о разности двух векторов, решим задачу.
Задача.
По
данным векторам  и
и
 построить вектор
построить вектор 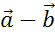 .
.
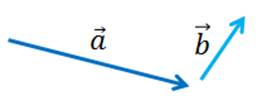
Построение
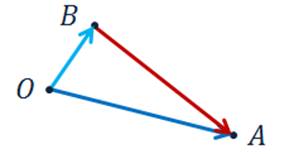
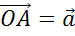
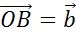
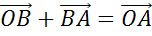
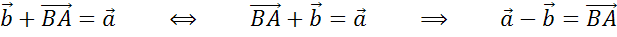 .
.
Вектор
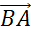 — искомый.
— искомый.
Эту задачу можно решить другим способом.
Но перед тем как его привести введём понятие вектора, противоположного данному.
Для
произвольного ненулевого вектора 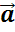 вектор
вектор
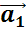 будет
противоположным, если:
будет
противоположным, если:
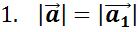
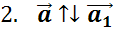
Вектор,
противоположный вектору 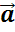 ,
обозначается так
,
обозначается так 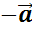 .
И говорят «вектор минус a».
.
И говорят «вектор минус a».
Очевидно, что сумма
вектора 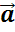 с
противоположным ему равна нулевому вектору
с
противоположным ему равна нулевому вектору 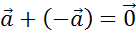 .
.
Запишем теорему о разности двух векторов.
Для
любых векторов  и
и
 справедливо
равенство
справедливо
равенство 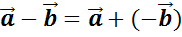 .
.
Докажем данную теорему.
Доказательство.
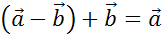
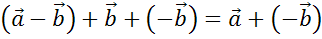
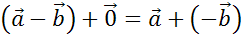
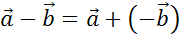
Что и требовалось доказать.
Опираясь
на эту теорему, приведём ещё одно решение задачи на построение разности
векторов 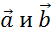 .
.
Способ
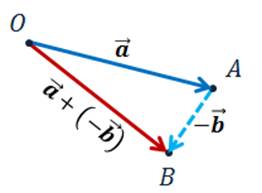
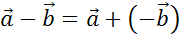
Отметим
произвольную точку О и от неё отложим вектор 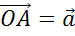 . Далее отложим от точки
А вектор
. Далее отложим от точки
А вектор 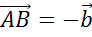 .
.
По
правилу треугольника сумма 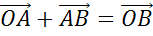 .
.
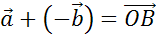
А
значит, пользуясь теоремой о разности двух векторов, можем сделать вывод о том,
что разность векторов 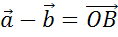 .
И вектор
.
И вектор 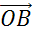 —
искомый.
—
искомый.
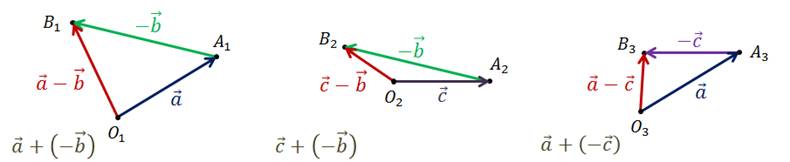
Итак, можем сделать вывод, что вектор разности двух векторов можно строить двумя способами.
Можно
от некоторой точки О отложить векторы 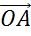 и
и 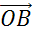 , равные векторам
, равные векторам 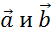 . При этом вектором их
разности будет вектор
. При этом вектором их
разности будет вектор 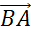 ,
направленный от конца вектора-вычитаемого к концу вектора-уменьшаемого.
,
направленный от конца вектора-вычитаемого к концу вектора-уменьшаемого.
Так
же, пользуясь теоремой о разности двух векторов, разность векторов 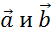 можно представить в
виде суммы вектора
можно представить в
виде суммы вектора 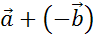 .
.
Тогда,
отложив от некоторой точки О вектор 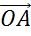 , равные вектору
, равные вектору  , а от точки А — вектор
, а от точки А — вектор 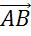 , равный вектору
, равный вектору 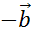 , по правилу треугольника
получим вектор
, по правилу треугольника
получим вектор 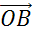 .
.
Он
является вектором суммы вектора 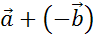 . И, соответственно,
вектором разности векторов
. И, соответственно,
вектором разности векторов 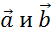 .
.
Задача.
Начертить попарно неколлинеарные векторы  ,
,  и
и 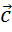 . Построить на них
векторы:
. Построить на них
векторы: 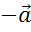 ,
,
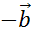 ,
, 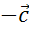 ,
, 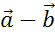 ,
, 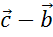 и
и 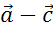 .
.
Построение.
Для начала построим векторы, противоположные данным.
Векторы являются противоположными, если их длины равны и они противоположно направлены.
Выберем точки А, B и C, от которых будем откладывать противоположные векторы.
Далее
через каждую из этих точек проведём прямые параллельные векторам  ,
,  и
и 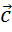 соответственно.
соответственно.
От
отмеченных точек на проведённых прямых можно изобразить векторы, равные данным,
и, противоположные данным. Нам нужны те, которые противоположны векторам  ,
,  и
и 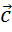 соответственно.
соответственно.
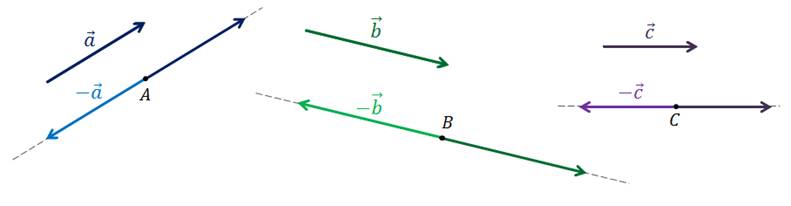
Так
мы построили векторы 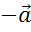 ,
,
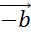 и
и 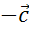 .
.
Задача.
Сторона квадрата 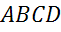 равна
равна
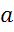 . Найти
. Найти 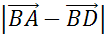 и
и 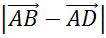 .
.
Построение.
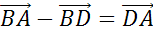
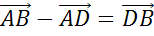
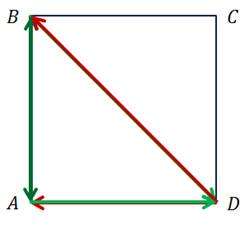
Решение.
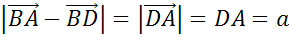
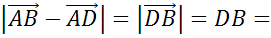
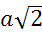
По
теореме Пифагора: 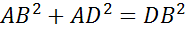
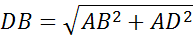
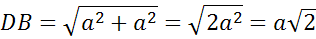
Ответ:
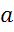 ;
; 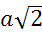 .
.
Подведём итоги нашего урока.
Сегодня вы познакомились с понятием противоположного вектора. Противоположные векторы имеют равные длины и противоположно направлены.
Мы
ввели понятие разности двух векторов. Разностью векторов  ,
,  называют такой
вектор
называют такой
вектор 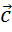 ,
сумма которого с вектором
,
сумма которого с вектором  равна вектору
равна вектору
 .
.
Для построения вектора разности мы выделили два способа.
Можно
от некоторой точки О отложить векторы 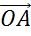 и
и 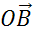 , равные векторам
, равные векторам  и
и  . При этом вектором их
разности будет вектор
. При этом вектором их
разности будет вектор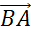 ,
направленный от конца вектора-вычитаемого к концу вектора-уменьшаемого.
,
направленный от конца вектора-вычитаемого к концу вектора-уменьшаемого.
Так
же, пользуясь теоремой о разности двух векторов, разность векторов  и
и  можно представить в
виде суммы вектора
можно представить в
виде суммы вектора  и
вектора, противоположного вектору
и
вектора, противоположного вектору  .
.
Тогда,
отложив от некоторой точки О вектор 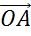 , равный вектору
, равный вектору  , а от точки А — вектор
, а от точки А — вектор 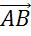 , равный вектору
, равный вектору 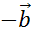 , по правилу треугольника
получим вектор
, по правилу треугольника
получим вектор 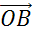 .
.
Он
является вектором суммы вектора  и вектора,
противоположного вектору
и вектора,
противоположного вектору  .
И, соответственно, вектором разности векторов
.
И, соответственно, вектором разности векторов  и
и  .
.
Теперь вы владеете не только правилами сложения, а ещё и правилом вычитания векторов.

 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 12167
12167



