Вам уже знакомы правило треугольника, правило параллелограмма и правило многоугольника сложения векторов.
Чтобы сложить
неколлинеарные векторы 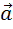 и
и
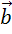 по
правилу треугольника, нужно от некоторой точки А отложить вектор
по
правилу треугольника, нужно от некоторой точки А отложить вектор 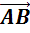 ,
равный вектору
,
равный вектору 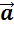 .
Далее от точки B отложить вектор
.
Далее от точки B отложить вектор 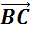 ,
равный вектору
,
равный вектору 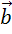 .
Вектор
.
Вектор 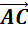 является
вектором суммы двух векторов
является
вектором суммы двух векторов 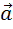 и
и
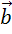 .
.
Для
сложения этих же векторов можно использовать правило параллелограмма. При этом
нужно отложить от произвольной точки А векторы 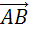 и
и
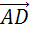 ,
равные векторам А
,
равные векторам А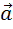 и
и
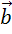 соответственно,
и построить на них параллелограмм ABCD.
Тогда вектор AC равен сумме векторов
соответственно,
и построить на них параллелограмм ABCD.
Тогда вектор AC равен сумме векторов 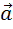 и
и
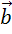 .
.
Для сложения нескольких векторов применяют правило многоугольника. При этом от некоторой точки последовательно откладывают векторы друг за другом, и вектором их суммы является вектор, проведённый от начала первого вектора к концу последнего.
Также вы владеете двумя способами построения вектора разности.
Можно
от некоторой точки О отложить векторы 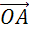 и
и
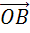 ,
равные векторам
,
равные векторам 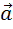 и
и
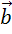 .
При этом вектором их разности будет вектор
.
При этом вектором их разности будет вектор 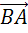 ,
направленный от конца вектора-вычитаемого к концу вектора-уменьшаемого.
,
направленный от конца вектора-вычитаемого к концу вектора-уменьшаемого.
Так
же, пользуясь теоремой о разности двух векторов, разность векторов 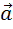 и
и
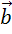 можно
представить в виде суммы вектора
можно
представить в виде суммы вектора 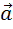 и
вектора, противоположного вектору
и
вектора, противоположного вектору 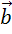 .
.
Тогда,
отложив от некоторой точки О вектор 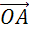 =
=
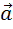 ,
а от точки А — вектор
,
а от точки А — вектор 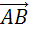 =
-
=
-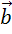 ,
по правилу треугольника получим вектор
,
по правилу треугольника получим вектор 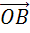 .
.
Он
является вектором суммы вектора 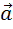 и
вектора, противоположного вектору
и
вектора, противоположного вектору 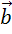 .
И, соответственно, вектором разности векторов
.
И, соответственно, вектором разности векторов 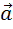 и
и
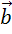 .
.
Сегодня мы познакомимся с ещё одним действием над векторами — умножением вектора на число.
Но, для начала, рассмотрим пример.
Парусник дрейфует прямолинейно с одной и той же скоростью, а один из лайнеров движется в попутном направлении со скоростью в пять раз большей. Второй лайнер движется им на встречу, то есть в противоположном направлении, с той же скоростью, что и первый лайнер.
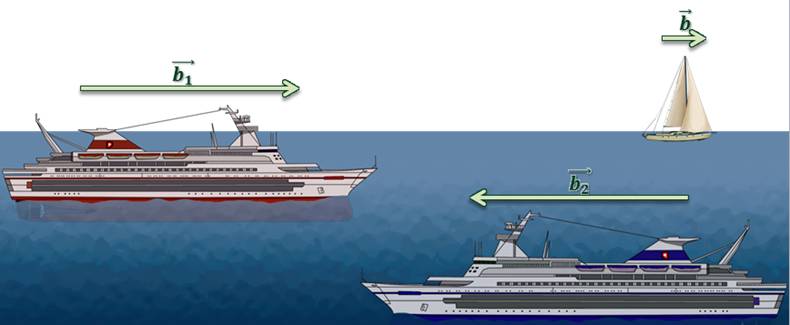
Если
изобразить скорость парусника вектором 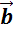 ,
то скорость первого лайнера, движущегося в попутном направлении, нужно
изобразить в виде сонаправленного вектора, длина которого в пять раз больше. И
выразить эту скорость можно через скорость b
умножением на 5.
,
то скорость первого лайнера, движущегося в попутном направлении, нужно
изобразить в виде сонаправленного вектора, длина которого в пять раз больше. И
выразить эту скорость можно через скорость b
умножением на 5.
Вектор
скорости второго лайнера должен иметь такую же длину, как и вектор скорости
первого лайнера, но он должен быть ему противоположно направленным. Значит, его
можно выразить через вектор 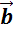 умножением
на -5.
умножением
на -5.
Этот пример поможет нам ввести понятие произведения вектора на число.
Определение.
Произведением
ненулевого вектора 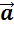 на
число
на
число 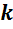 называется
такой вектор
называется
такой вектор 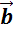 ,
длина которого равна
,
длина которого равна 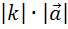 .
Причем
.
Причем 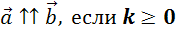 ,
,
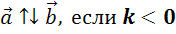 .
.
Произведение
числа 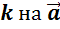 обозначают
так
обозначают
так 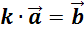 .
.
Следствия.
1.
Произведение
вектора 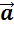 на
ноль, равно нулевому вектору
на
ноль, равно нулевому вектору 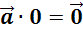 .
.
2.
Ненулевой вектор 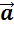 коллинеарен вектору, заданному произведением данного вектора
коллинеарен вектору, заданному произведением данного вектора
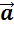 на число k
на число k 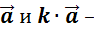 коллинеарны.
коллинеарны.
Ведь, если 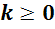 , то полученный вектор сонаправлен вектору
, то полученный вектор сонаправлен вектору 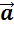 , а если
, а если 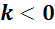 , то он противоположно направлен ему. Но в каждом из этих случаев
они будут коллинеарны.
, то он противоположно направлен ему. Но в каждом из этих случаев
они будут коллинеарны.
По
данному вектору 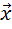 построить
векторы:
построить
векторы: 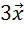 ;
;
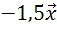 ;
;
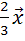 ;
;
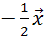 .
.
Длина вектора 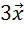 должна
быть в три раза больше длины вектора
должна
быть в три раза больше длины вектора 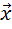 .
И этот вектор будет сонаправлен вектору
.
И этот вектор будет сонаправлен вектору 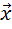 ,
ведь k в данном случае равно
трём, а это больше нуля.
,
ведь k в данном случае равно
трём, а это больше нуля.
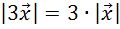 ;
;
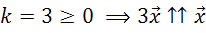 .
.

Далее изобразим вектор 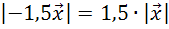 ,
,
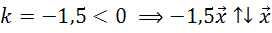 .
.

Длина вектора 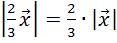 ,
,
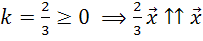 .
.

Последним
построим вектор 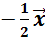 .
.
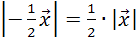 ,
,
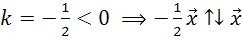 .
.

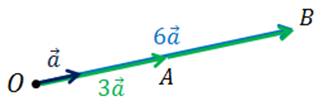
Чтобы умножить вектор 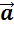 на произведение чисел k и l, можно вектор
на произведение чисел k и l, можно вектор 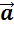 сначала умножить на число l, а затем на число k:
сначала умножить на число l, а затем на число k: 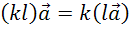 . Этот закон называют сочетательным, и его можно проиллюстрировать
так.
. Этот закон называют сочетательным, и его можно проиллюстрировать
так.
Рассмотрим случай, когда 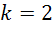 ,
, 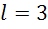 :
: 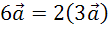 .
.
Вторым
свойством запишем, что 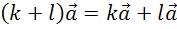 .
Это первый распределительный закон.
.
Это первый распределительный закон.
Проиллюстрируем его.
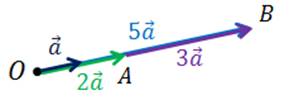
Также рассмотрим случай,
когда 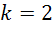 ,
, 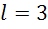 :
: 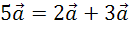 .
.
Запишем
второй распределительный закон 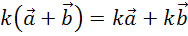 .
.
Например,
если рассмотреть подобные треугольники 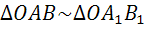 с
коэффициентом подобия k,
то можно записать, что вектор
с
коэффициентом подобия k,
то можно записать, что вектор 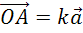 ,
вектор
,
вектор 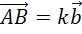 ,
а вектор
,
а вектор 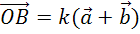 .
.
С
другой стороны вектор 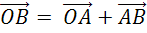 .
Отсюда получаем, что произведение
.
Отсюда получаем, что произведение 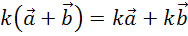 .
.
Данные свойства произведения вектора на число позволяют выполнять преобразования в выражениях, содержащих суммы, разности векторов и произведения векторов на числа, так же как и в числовых выражениях.
Преобразуем выражения с векторами с помощью известных свойств.
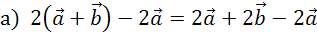
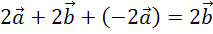
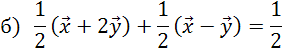
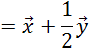
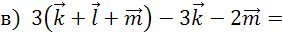
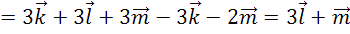
Можно сделать вывод, что над выражениями с векторами можно выполнять все те же преобразования, что и над алгебраическими выражениями.
Задача. Начертить
попарно неколлинеарные векторы 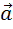 ,
,
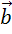 и
и
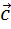 .
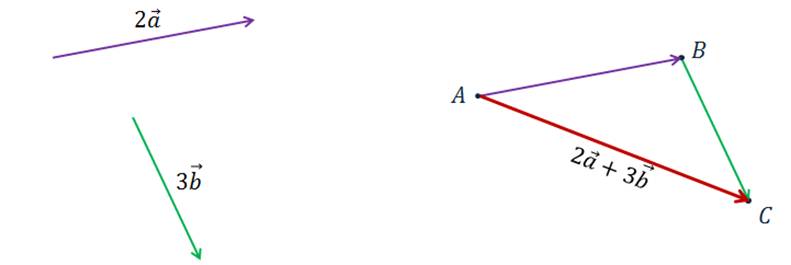
Построить векторы
.
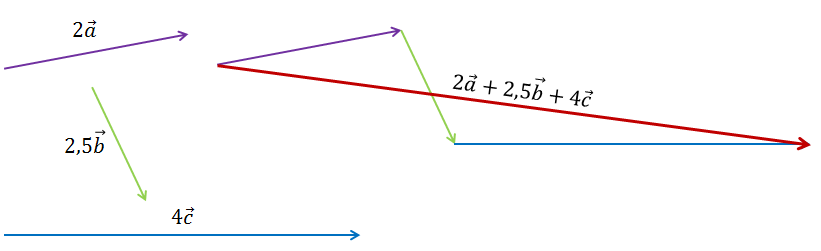
Построить векторы 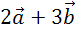 ,
,
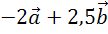 и
и
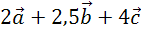 .
.
Построение.

Подведём итоги нашего урока.
Сегодня вы познакомились с новым действием над векторами: умножением вектора на число.
Произведением
ненулевого вектора 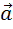 на
число k называется такой вектор
на
число k называется такой вектор 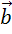 ,
длина которого равна произведению модуля числа k
и длины данного вектора
,
длина которого равна произведению модуля числа k
и длины данного вектора 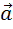 .
Причем векторы
.
Причем векторы 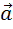 и
и
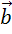 сонаправлены,
если k больше
либо равно 0, и противоположно направлены, если k
меньше
0.
сонаправлены,
если k больше
либо равно 0, и противоположно направлены, если k
меньше
0.
Также записали два следствия из определения:
произведение
вектора 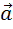 на
ноль, равно
на
ноль, равно 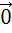 ;
;
ненулевой вектор 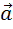 коллинеарен вектору, заданному произведением данного вектора
коллинеарен вектору, заданному произведением данного вектора
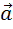 на число k.
на число k.
Исходя из того, что произведение вектора на число обладает тремя свойствами, мы получили сочетательный закон, а также первый и второй распределительные законы.
Они позволяют выполнять преобразования в выражениях, содержащих суммы, разности векторов и произведения векторов на числа, так же как и в числовых выражениях.

 Получите свидетельство
Получите свидетельство Вход
Вход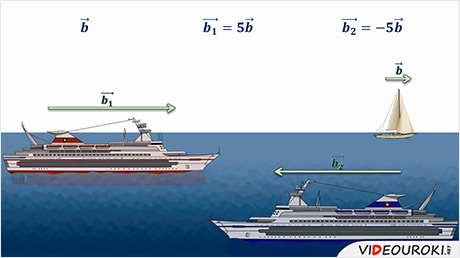



 0
0 10446
10446

