Импульс. Закон сохранения импульса

Уже достаточно длительное время мы с вами рассматриваем три закона Ньютона, с помощью которых можно решить большой спектр задач, связанных с нахождением кинематических величин движущегося тела по известным действующим силам. Как сказал выдающийся физик Ричард Фейнман: «Вся классическая механика содержится в этих законах».

Давайте рассмотрим простой пример. Пусть под действием постоянной силы в течение некоторого промежутка времени скорость тела изменяется от υ₁ до υ₂.

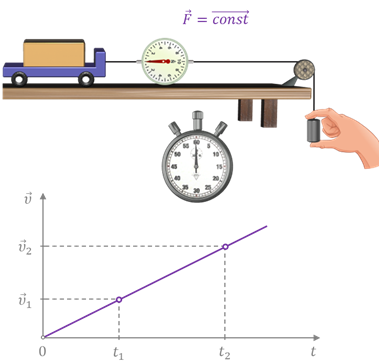
Согласно второму закону Ньютона, единственным результатом действия этой силы будет сообщение телу ускорения, которое, как известно, равно отношению изменения скорости тела к промежутку времени, в течение которого это изменение произошло:

Умножим это равенство на промежуток времени, в течение которого действовала сила, и раскроем скобки:

Вы уже знаете, что величину, равную произведению массы тела на его скорость, называют импульсом тела или количеством движения.

Импульс — это векторная величина. А так как масса тела — величина скалярная и всегда больше нуля, то из формулы следует, что направление вектора импульса тела совпадает с направлением вектора его скорости.

Единицей измерения импульса в СИ:

Понятие импульса (а точнее, количества движения) было введено в первой половине XVII века Рене Декартом. Но так как физического понятия массы в то время ещё не было, то он определял импульс как «произведение величины тела на скорость его движения». Причём под скоростью понимался лишь её модуль, в то время как её направление не учитывалось. В 1668 году английский математик Джон Уоллис предложил считать количество движения не скалярной, а направленной величиной, учитывая направления с помощью знаков «плюс» и минус».

А в 1686 году в «Математических началах натуральной философии» Ньютон уточнил понятие импульса: количество движения есть мера токового, устанавливаемая пропорционально скорости и массе.

Давайте перепишем основное уравнение динамики с учетом определения импульса тела

Произведение силы на время ее действия называется импульсом силы. А полученная нами формула выражает второй закон Ньютона в более общей формулировке: изменение импульса тела (а точнее, материальной точки) равно импульсу равнодействующей сил, действующих на него.

Теперь давайте с вами посмотрим, как изменяется импульс нескольких взаимодействующих тел. Сразу же напомним, что в механике всякая группа тел или совокупность частей одного и того же тела, взаимодействующих между собой, называется механической системой.

Рассмотрим упрощённую модель колыбели Ньютона, состоящую только из двух шаров одинаковой массы.

Будем считать, что сопротивление воздуха отсутствует. Тогда если отклонить один из них на небольшой угол и отпустить, то, вернувшись в своё начальное положение, он ударит по второму шару и остановится. А вот второй шар придёт в движение и, что самое интересное, отклонится от своего начального положения на такой же угол, на который мы отклонили первый шар. В дальнейшем такое движение шаров будет повторяться бесконечно долго. При этом очевидно, что в результате взаимодействия импульс шаров постоянно менялся. Но на сколько уменьшался импульс одного шара, на столько же увеличивался импульс другого.

В нашем примере между взаимодействующими телами действовали только силы, входящие в данную систему. Напомним, что такие силы принято называть внутренними, а механическую систему — замкнутой.

Если же на систему тел действуют ещё и сторонние силы, называемые внешними, то механическая система считается незамкнутой.

Примером почти замкнутой системы является наша Солнечная система. В ней движения планет происходят за счёт силы притяжения Солнца и сил притяжения друг к другу. Но вот система, состоящая, например, только из Солнца, Земли и Луны, является незамкнутой. Подумайте, почему?

А теперь давайте с вами рассмотрим незамкнутую систему, состоящую из трёх тел, на которые действуют внешние силы.

Запишем для каждого из тел уравнение движения в импульсной форме:

И просуммируем их.

Второе слагаемое, стоящее в правой части полученного уравнения, равно нулю, так как согласно третьему закону Ньютона силы взаимодействия между телами равны по модулю и противоположны по направлению:

В скобках левой части уравнения у нас стоит векторная сумма импульсов тел, входящих в систему. Она называется импульсом системы. То есть импульс системы тел равен векторной сумме импульсов тел, входящих в данную систему.

Отсюда следует, что изменение импульса механической системы тел равно импульсу результирующей внешних сил. Иными словами, только внешние силы могут изменить импульс механической системы.

Внутренние же силы способны изменить только импульс отдельных тел, входящих в систему. Но изменить суммарный импульс системы они не могут. Поэтому в случае замкнутой системы изменение её импульса равно нулю. Отсюда вытекает один из фундаментальных законов природы — закон сохранения импульса: геометрическая сумма импульсов всех тел, входящих в замкнутую систему, остается неизменной при любых движениях и взаимодействиях тел системы.

Конечно же реальные системы никогда не бывают за́мкнутыми. Так на любое тело, находящееся у поверхности Земли, действует сила её притяжения. А на Землю действуют силы притяжения Солнца и других планет нашей Солнечной системы. В свою очередь, на неё действуют миллиарды звёзд Млечного Пути. Но и галактики не являются замкнутыми системами, так как они тоже взаимодействуют между собой силами всемирного тяготения.

Однако закон сохранения импульса применим и для незамкнутых систем, если результирующая внешних сил, действующих на систему, равна нулю. Применять его можно и тогда, когда внутренние силы гораздо больших внешних. Например, это может быть соударение тел, разрыв снарядов и тому подобное.

И наконец, закон сохранения импульса можно применять в том случае, когда сумма проекций внешних сил на любое направление равна нулю, даже если геометрическая сумма внешних сил отлична от нуля.

Большое значение закон сохранения импульса имеет для исследования реактивного движения. Давайте вспомним, что реактивным называется движение тела, возникающее при отделении некоторой его части с определённой скоростью относительного него.

Примером реактивного движения является движение ракеты. Так как вследствие истечения струи ракета движется с ускорением, то можно считать, что на ракету действует сила, которую принято называть реактивной силой. Её главная особенность заключается в том, что она возникает в результате взаимодействия частей системы без какого-либо взаимодействия с внешними телами.

Эта особенность очень важна для космических полётов, так как в космосе нет среды, от которой можно «отталкиваться» и получать ускорение.  Поэтому единственная возможность достичь космических скоростей и управлять движением космических аппаратов — это использование реактивных двигателей. Их теория была разработана в начале ХХ века выдающимся русским учёным Константином Эдуардовичем Циолковским.

А воплощены в жизнь — 4 октября 1957 года советскими инженерами и конструкторами под управлением Сергея Павловича Королёва. Именно в этот день состоялся запуск первого в мире искусственного спутника Земли.

А уже 12 апреля 1961 года состоялся исторический запуск космического корабля «Восток-1» с первым человеком на борту. Его имя хорошо известно во всех странах мира — это Юрий Алексеевич Гагарин.