Мы с вами уже знаем, что Квадратным
уравнением называется уравнение вида  ,
где
,
где  –
переменная,
–
переменная,  ,
,
 и
и
 –
некоторые числа, причем
–
некоторые числа, причем  .
.
В алгебре, геометрии, физике и др. науках очень часто решение задачи сводится к нахождению корней квадратных уравнений. Поэтому очень важно научиться решать квадратные уравнения.
Решить уравнение:

Мы с вами решили это уравнение методом выделения полного квадрата, т.е. применили формулу квадрата разности.
Решить уравнение:
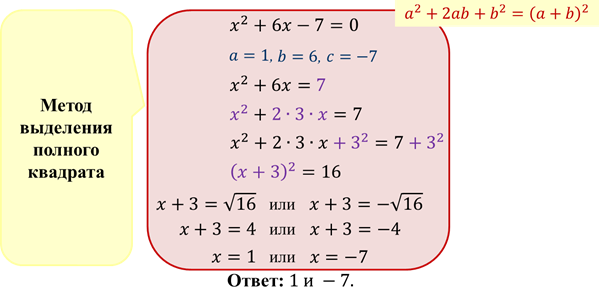
Мы снова нашли корни уравнения методом выделения полного квадрата. Но этот метод частенько приводит к громоздким преобразованиям. Поэтому древние математики вывели формулу корней квадратного уравнения, которую можно применять при решении любого квадратного уравнения.
Можно получить эти формулы, решая квадратное уравнение в общем виде методом выделения полного квадрата.
Итак, рассмотрим
квадратное уравнение общего вида  , где
, где  .
.

Мы с вами определили, что знак дроби, записанной в правой части уравнения зависит от знака дискриминанта. Поэтому при решении этого уравнения возможны три случая.
Первый случай:

Вывод: уравнение  , при
, при  , имеет два различных корня. Которые находят по формулам:
, имеет два различных корня. Которые находят по формулам:

Обычно эти формулы объединяют в одну, записывая её следующим образом:

Второй случай:

Вывод: уравнение  , при
, при  ,имеет единственный корень. Который вычисляется по формуле:
,имеет единственный корень. Который вычисляется по формуле:

Третий случай:
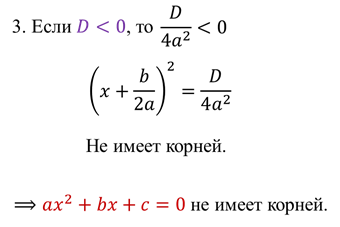
Вывод: уравнение
 , при
, при  ,не имеет корней.
,не имеет корней.
Таким образом: в зависимости от значения дискриминанта квадратное уравнение  , может иметь:
, может иметь:
1.
Два различных корня: 
 . При
. При  .
.
2.
Один корень:  . При
. При  .
.
3.
Не имеет корней. При  .
.
Запишем алгоритм решения квадратных уравнений.

Задание: решить уравнения.

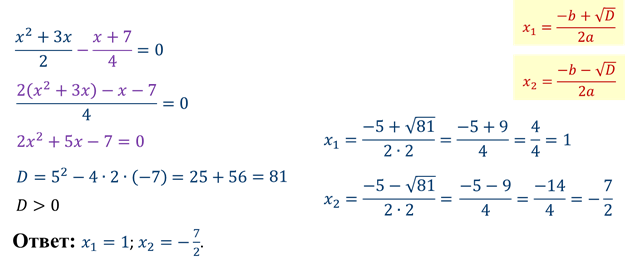
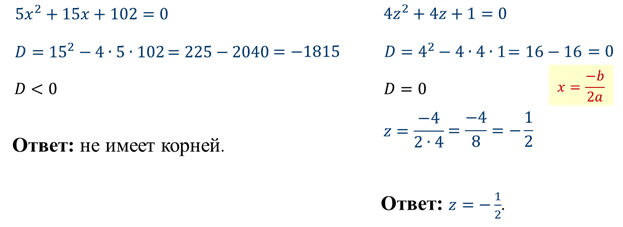
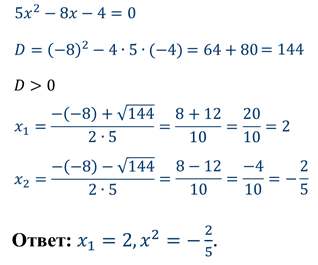
Обратите внимание, второй коэффициент в начальном уравнении чётный. Есть формула корней квадратного уравнения с чётным вторым коэффициентом. С помощью неё удобнее вычислять корни. Давайте выведем её.
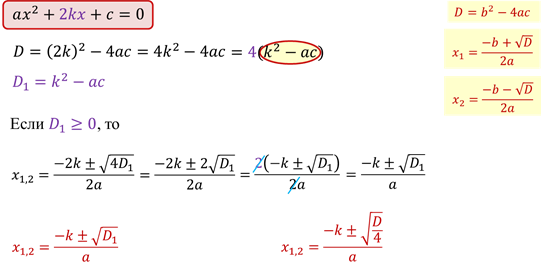
Давайте найдём корни последнего уравнения по новой формуле.
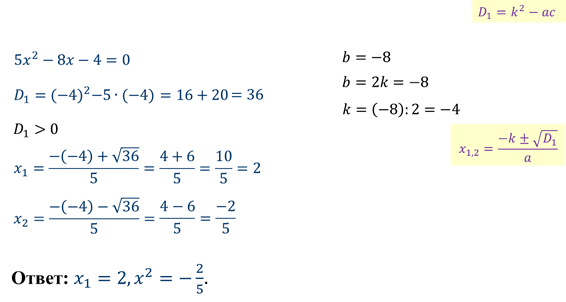
Итоги:
Выражение  называется
дискриминантом квадратного уравнения.
называется
дискриминантом квадратного уравнения.
При решении квадратного уравнения возможны три случая в зависимости от знака дискриминанта:
1)
Если  ,
то уравнение имеет два различных корня, которые вычисляются по формуле:
,
то уравнение имеет два различных корня, которые вычисляются по формуле:  .
.
2)
Если  ,
то уравнение имеет единственный корень, который вычисляется по формуле
,
то уравнение имеет единственный корень, который вычисляется по формуле  .
.
3)
Если  ,
то уравнение не имеет корней.
,
то уравнение не имеет корней.

 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 12979
12979

