Решение задач с помощью квадратных уравнений

В алгебре, геометрии, физике и др. науках очень часто решение задач сводится к нахождению корней квадратных уравнений. Решение квадратных уравнений особых трудностей не вызывает, если знать основные формулы.

Поэтому очень важно при решении задач научиться составлять квадратные уравнения, т.е. переводить условия задач на математический язык.

Решение несколько задач, которые сводятся к решению квадратных уравнений.

Задача 1. В зрительном зале рядов в 2 раза больше, чем мест в каждом ряду. Если при перепланировке зала число рядов увеличить на 1, а число мест в каждом ряду увеличить на 8, то в зале будет 500 мест. Сколько мест в зале?

Решение:

Обозначим за  – число мест в ряду. Тогда  – число рядов. Число мест после перепланировки будет , а число рядов . Так как по условию задачи после перепланировки число мест в зале будет равно , то можем составить уравнение:

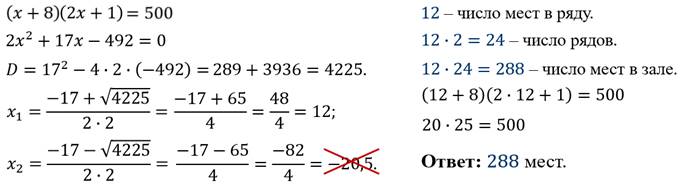
Задача 2. Гипотенуза прямоугольного треугольника равна 10 см. Найдите его катеты, если их сумма равна 14 см.

Решение:

По теореме Пифагора , где  и  – катеты,  – гипотенуза. Пусть  (см) – длина одного из катетов. Тогда  см – длина второго катета. По условию задачи известно что гипотенуза прямоугольного треугольника равна  см. Составим уравнение:

Задача 3. Мяч брошен вертикально вверх с начальной скоростью 30 м/с. Считая ускорение земного притяжения равным 10 м/с в квадрате и не учитывая сопротивление воздуха, найдите, через сколько секунд мяч будет на высоте 25 м.

Решение.

Итоги:

Итак, мы решили несколько разных текстовых задач. Обратите внимание, что оформлять решения задач можно и значительно короче. Только необходимо показать, какое неизвестное обозначается буквой. Записать уравнение. Решить его. И сделать вывод о том, удовлетворяют ли найденные корни условию задачи. Ну и, конечно же, не забыть ответить на вопрос задачи.