Теорема Виета

Решим уравнение: .

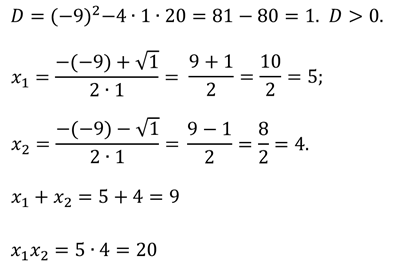
Если внимательно посмотреть на коэффициенты этого квадратного уравнения, то можно увидеть, что сумма корней, которую  нашли, равна второму коэффициенту. Правда, только взятому с противоположным знаком. А произведение этих корней равно свободному члену. Так вот таким свойством обладает любое приведенное квадратное уравнение.

Теорема: сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

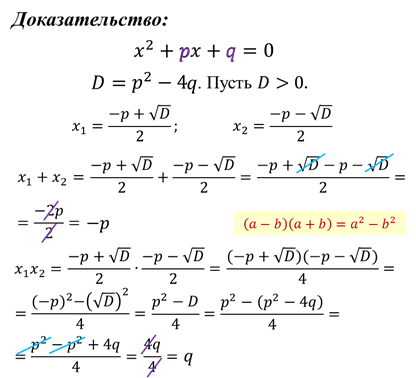
Т.е. мы с вами показали, что сумма корней равна второму коэффициенту, взятому с противоположным знаком, а произведение этих же корней равно свободному члену уравнения. Значит, теорема доказана.

При дискриминанте равном нулю квадратное уравнение имеет один корень. Но если считать, что когда дискриминант равен нулю, уравнение имеет два равных корня, то теорема будет верна и в этом случае. Это следует из того, что при дискриминанте равном нулю корни уравнения также можно найти по формуле:

Теорему, которую  доказали, называют теоремой Виета. Соотношения корней впервые обнаружил французский математик Франсуа Виет.

Франсуа Виет внёс большой вклад в развитие математики. По существу он создал новую алгебру. Виет ввёл в неё буквенную символику и показал, как, оперируя символами, можно получить результат, который применим к любым соответствующим величинам, т.е. решить задачу в общем виде. Это положило начало коренному перелому в развитии алгебры: стало возможным буквенное исчисление. Так, в частности, он предложил использовать буквы для обозначения коэффициентов. Самым важным своим открытием Виет считал установление связи между координатами и коэффициентами уравнений.

Пусть квадратное уравнение  имеет корни  и . Равносильное ему приведенное квадратное уравнение имеет вид:

И, следовательно, имеет те же корни.

С помощью теоремы Виета можно решать многие квадратные уравнения устно, не пользуясь громоздкими формулами корней.

Задание 1: не решая уравнения, найти сумму и произведение корней, если они существуют.

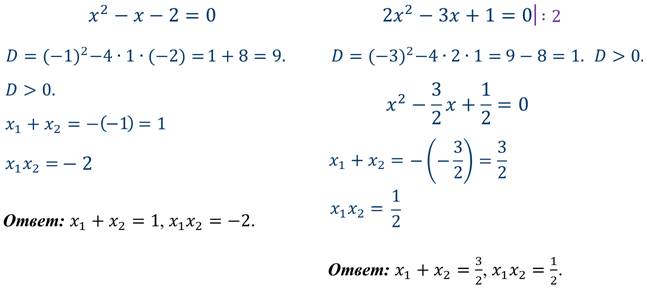
Задание 2: найти подбором корни уравнения.

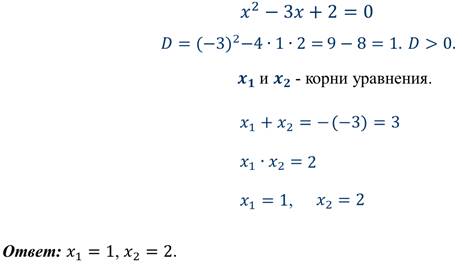
Итоги:

На этом уроке познакомились с теоремой Виета, которая имеет следующую формулировку: сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.