Обратная теорема Виета

Мы с вами уже знаем теорему Виета. Вспомним её формулировку: сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

Справедлива также теорема обратная теореме Виета. Запишем её формулировку. Если числа  и  таковы, что их , а , то эти числа являются корнями квадратного уравнения .

С помощью обратной теоремы Виета удобно проверять, правильно ли найдены корни квадратного уравнения, а также по указанным корням составлять уравнения.

Задание: найдите корни уравнения и выполните проверку по теореме, обратной теореме Виета.

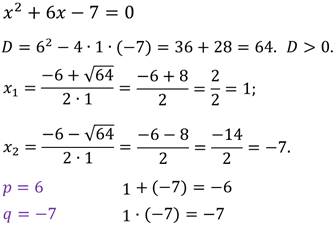
И выполним обратное задание: составьте квадратное уравнение по его корням.

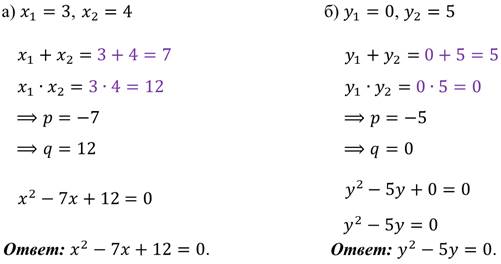
Задание: один из корней уравнения  равен четырем. Найдите другой корень и коэффициент .

Решение:

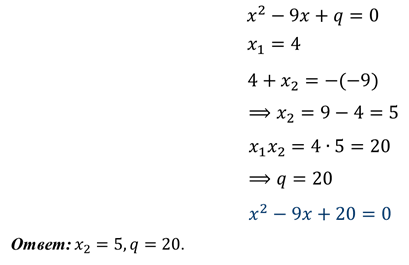
Задание: один из корней уравнения  равен минус пяти. Найдите другой корень и коэффициент .

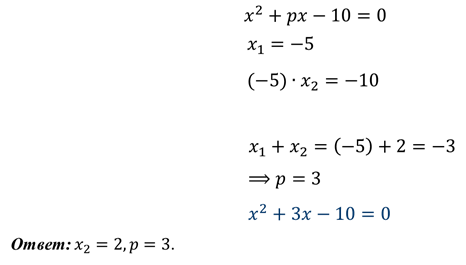
Итоги:

Сегодня на уроке мы познакомились с обратной теоремой Виета, которая имеет следующую формулировку: если числа  и  таковы, что их сумма равна , а произведение равно , то эти числа являются корнями квадратного уравнения .