В жизни мы часто сталкиваемся с людьми, которые говорят только правду и с людьми, которые любят пошутить.

Чтобы узнать правдивость тех или иных высказываний можно использовать разные способы.
Сегодня на уроке мы с вами научимся выяснять правду на примере некоторых задач с помощью таблицы истинности, логических операций и законов алгебры логики.
Итак, давайте рассмотрим первую задачу.
Ученики писали контрольную работу по физике. На контрольной работе из-за болезни не было трёх ребят: Пети, Жени и Саши.



Им пришлось писать контрольную работу отдельно от всего класса. Петя сказал, что он не написал на 5 и Женя не написал на 5. Женя сказал, что Петя не написал на 5, а Саша написал на 5. Саша сказал, что он не написал на 5, а Петя написал на 5. После проверки работ стало известно, что только один из учащихся написал контрольную работу на 5. Оказалось, что один из учеников был прав, второй нет, а третий в одном утверждении прав, а во-втором – нет. Давайте узнаем кто был прав, и кто написал контрольную на пять?
Перейдём к решению. Обозначим каждого из мальчиков первыми буквами их имён.



Так как у нас сказано, что только один из мальчиков написал на пять, то предположим следующее:
П = «Петя написал на 5».
Ж = «Женя написал на 5».
С = «Саша написал на 5».
Давайте для решения этой задачи составим таблицу истинности. Она будет состоять из 9 столбцов, которые будут содержать имена трёх мальчиков и их высказываний.

Высказываний у нас 6:
П1 = «Петя не написал на 5».
П2 = «Женя не написал на 5».
Ж1 = «Петя не написал на 5».
Ж2 = «Саша написал на 5».
С1 = «Саша не написал на 5».
С2 = «Петя написал на 5».
Для удобства над каждым высказыванием подпишем, кто это говорил. Если какое-то высказывание является отрицательным, то его будем обозначать знаком инверсии.

Далее нужно определиться с количеством строк. Так как 5 получил только один из трёх учащихся, то для того, чтобы узнать, кто это был, достаточно фрагмента таблицы. В нём будут содержаться следующие наборы входных значений:
0 0 1
0 1 0
1 0 0
Введём их в нашу таблицу.

Если внимательно посмотреть на первых три столбца, то мы можем увидеть, что предполагается, что один из учащихся написал контрольную на 5, в то время, как два других не написали на 5.
Идём дальше. Петя уверен, что он не написал на 5. Применяем инверсию к первому столбцу и запишем данные в четвёртый.

Дальше Петя сказал, что Женя не написал на 5. В этом случае будем применять инверсию к данным из второго столбца.

Шестой столбец заполним исходя из высказывания Жени, что Петя не написал на 5 и применим инверсию к первому столбцу.

Далее Женя уверен, что Саша написал на 5. Перепишем данные из третьего столбца в седьмой.

Аналогично заполним два оставшихся столбца.

Так как у нас известно, что один из учащихся был прав, второй – нет, а третий лишь на половину, то нам нужно искать строку, в которой в любом порядке содержатся комбинации значений 00, 11, 01 или 10. Это третья строка нашей таблицы.

Исходя из этой строки можно сделать вывод, что Петя получил 5 за контрольную по физике, а прав был в своих утверждениях Саша.
Решим ещё одну задачу с помощью логических операций и законов алгебры логики.
Три учителя решили выяснить, кто бегал по корриду на перемене и разбил вазон с цветком. Ирина Николаевна утверждает, что это был восьмиклассник в красной рубашке.

Анна Семёновна сказала, что это был шестиклассник в синей рубашке.

А Алексей Александрович видел, что это был учащийся седьмого класса, но точно не в красной рубашке.

Когда виновника нашли, выяснилось, что каждый из учителей описал верно только один признак, по которому можно было узнать, кто это был, а со вторым – ошибся. Из какого класса был ученик, и во что он был одет?
Перейдём к решению. Для начала запишем каждое высказывание и обозначим его при помощи переменных. Получим следующее:
А = «Ученик был в красной рубашке».
B = «Это был учащийся восьмого класса».
С = «Учащийся был одет в синюю рубашку».
D = «Это был учащийся шестого класса».
Е = «Это был учащийся седьмого класса».
Со слов Ирины Николаевны следует, что A V B истинно, то есть A V B = 1. Со слов Анны Семёновны следует, что C V D истинно, то есть C V D = 1. А со слов Алексея Александровича следует, что Ā V E также истинно, то есть Ā V E = 1.
Следовательно, будет истинна конъюнкция всех трёх выражений:
(A V B) & (C V D) & (Ā V E) = 1.
Раскроем первых две скобки, используя распределительный (дистрибутивный) закон, заменим конъюнкцию знаком умножения, а дизъюнкцию – знаком сложения. Получим следующее:
(A · C + A · D + B · C + B · D) · (Ā + E) = 1.
Раскроем оставшиеся скобки:
A · C · Ā + A · D · Ā + B · C · Ā + B · D · Ā + A · C · E + A · D · E + B · C · E + B · D · E = 1.
Мы получили 8 слагаемых, сумма которых равных 1. Давайте рассмотри каждое из них. Первое: A · C · Ā. Исходя из пятого закона исключённого третьего, первое слагаемое будет ложным, так как A и Ā дают сами по себе ложный результат. Соответственно всё это выражение становится ложным:
A · C · Ā = 0.
Аналогично и со вторым выражением:
A · D · Ā = 0.
Оно также ложно.
Следующее выражение: B · C · Ā. В – говорит о том, что учащийся был восьмого класса. С – учащийся был одет в синюю рубашку. Ā – ученик был не в красной рубашке. Это говорит о том, что третье выражение является истинным, так как ничто и ничему не противоречит. Обведём его.
Далее B · D · Ā. В – говорит о том, что учащийся был восьмого класса. D – учащийся был из шестого класса. Ученик не может одновременно учиться и в восьмом и в шестом классе. Значит наше выражение ложно:
B · D · Ā= 0.
A · C · E также ложно: A · C · E = 0. Учащийся не может быть одновременно в синей и красной рубашках.
Выражение A · D · E = 0, то есть ложно. Ученик не может учится и в шестом и в седьмом классах.
Остальные выражения также ложны:
B · C · E = 0.
B · D · E = 0.
У нас получилось одно единственное истинное высказывание: B · C · Ā = 1.
Из последнего равенства можно сказать, что:
В = 1;
С = 1;
Ā = 1.
Это говорит о том, что истинными будут выражения: «Это был учащийся восьмого класса»; «Учащийся был одет в синюю рубашку»; «Ученик был не в красной рубашке».
Ответ на задачу будет такой: это был ученик восьмого класса в синей рубашке.
Для закрепления давайте решим ещё две задачи.
Задача три: одиннадцатиклассники Лёша, Руслан и Андрей руководили математическим кружком учащихся третьих классов.

На одном из занятий они предложили ребятам решить логическую задачу, которую составил один из них. На вопрос, кто же составил задачу, каждый дал свой ответ.
Андрей: «Я не составлял. Руслан не составлял».

Руслан: «Андрей не составлял. Задачу составил Лёша».

Лёша: «Я не составлял. Задачу составил Андрей».

Известно, что один из них оба раза говорил правду (назовём его правдивым), второй оба раза сказал неправду (назовём его шутником), третий – один раз сказал правду, а второй раз – неправду (назовём его хитрецом). Необходимо назвать имена правдивого, шутника и хитреца. А также того, кто составил задачу.
Перейдём к решению. И снова составим таблицу истинности. Она будет состоять из 9 столбцов, которые будут содержать первые буквы имён трёх мальчиков и их высказываний.

Высказываний у нас 6:
Л1 = «Лёша не составлял».
Л2 = «Задачу составил Андрей».
Р1 = «Андрей не составлял».
Р2 = «Задачу составил Лёша».
А1 = «Андрей не составлял».
А2 = «Руслан не составлял».
Для удобства над каждым высказыванием подпишем, кто это говорил. Если какое-то высказывание является отрицательным, то будем обозначать знаком инверсии.

Количество строк в таблице будет равно 3, так как задачу составлял только один из трёх учащихся. То есть для того, чтобы узнать, кто это был, достаточно фрагмента таблицы.

В нём будут содержатся следующие наборы входных значений:
0 0 1
0 1 0
1 0 0
Введём их в нашу таблицу.

Так как задачу составил один из учащихся, то у каждого учащегося в столбце будет стоять одна единица и два нуля. Если посмотреть по строкам или столбцам, то единица встречается один раз, а ноль – два.
Идём дальше. Лёша сказал, что не он составлял задачу. Применяем инверсию к первому столбцу и запишем данные в четвёртый.

Дальше Лёша сказал, что Андрей составлял задачу. Перепишем данные из третьего столбца в пятый.

Аналогично заполняем всю таблицу.

Так как у нас известно, что один из учащихся был прав, второй – нет, а третий лишь на половину, то нам нужно искать строку, в которой в любом порядке содержатся комбинации значений 00, 11, 01 или 10. Это первая строка нашей таблицы.

Исходя из этой строки можно сделать вывод, что Андрей составил задачу. Имя правдивого – Лёша, шутника – Руслан, а хитреца – Андрей.
Мы с вами решили задачу с использованием таблицы истинности.
Задача 4. Витя, Рома и Артём ходили на рыбалку.

Они поймали одну рыбу. Придя домой каждый из них сказал бабушке следующее:
Витя: «Это карась длиной 7 сантиметров».

Рома: «Это щука длиной 10 сантиметров».

Артём: «Это не карась длиной 5 сантиметров».

После того, как бабушка посмотрела в ведро с рыбой, она сказала, что каждый из них сказал правду только один раз. Второе же предположение было ложно. Какую рыбу поймали мальчики и какой длины?
Переходим к решению. Обозначим каждое высказывание при помощи переменных. Получим следующее:
А = «Карась».
B = «Семь сантиметров».
C = «Щука».
D = «Десять сантиметров».
Е = «Пять сантиметров».
Со слов Вити выходит, что A V B истинно, то есть A V B = 1. Со слов Ромы – C V D истинно, то есть C V D = 1. Со слов Артёма – Ā V E истинно, то есть Ā V E = 1.
Из этого можно прийти к выводу, что будет истинна конъюнкция всех трёх выражений, и она будет равна единице:
(A V B) & (C V D) & (Ā V E) = 1.
Теперь давайте упростим наше выражение и раскроем первые две скобки, используя распределительный (дистрибутивный) закон, а также заменим конъюнкцию знаком умножения, а дизъюнкцию – знаком сложения. Получим следующее:
(A · C + A · D + B · C + B · D) · (Ā + E) = 1.
А теперь раскроем все скобки:
A · C · Ā + A · D · Ā + B · C · Ā + B · D · Ā + A · C · E + A · D · E + B · C · E + B · D · E = 1.
У нас получилось 8 выражений. Давайте каждое из них рассмотрим в отдельности.
A · C · Ā будет ложным, так как рыба не может одновременно быть карасём и не быть им.
Далее A · D · Ā также будет ложным.
B · C · Ā будет истинным, так как исходя из этого выражения следует, что мальчики словили щуку, 7 сантиметров и это не карась.
B · D · Ā будет ложно. Так как рыба не может быть равна 7 и 10 сантиметров одновременно.
При рассмотрении оставшихся выражений мы можем увидеть, что все они ложны:
A · C · E = 0.
A · D · E = 0.
B · C · E = 0.
B · D · E = 0.
Мы с вами получили выражение B · C · Ā = 1. Это говорит о том, что истинными будут выражения: «7 сантиметров»; «Щука»; «Не карась».
Ответ на задачу следующий: это была щука длиной 7 сантиметров.
Пришла пора подвести итоги урока. Сегодня мы научились решать логические задачи с помощью таблиц истинности, а также логических операций и законов алгебры логики.

 Получите свидетельство
Получите свидетельство Вход
Вход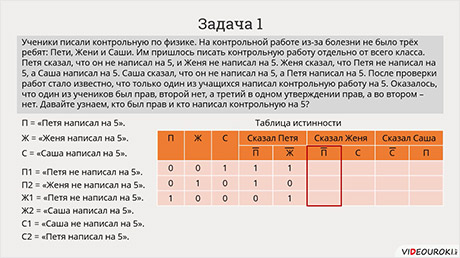




 31403
31403

