Мы с вами знаем следующие логические операции: конъюнкция (логическое умножение), дизъюнкция (логическое сложение) и инверсия (отрицание). Все эти операции используются в алгебре логики.
Сегодня на уроке мы с вами узнаем, что такое логический элемент, познакомимся с такими логическими элементами, как конъюнктор, дизъюнктор и инвертор. А также научимся находить выходные данные исходя из предоставленной электронной схемы.
Алгебра логики является незаменимым элементом в конструировании автоматических устройств, разработке аппаратных и программных средств информационных и коммуникационных технологий.
Мы с вами уже знаем, что любую информацию можно представить в дискретной форме. Дискретная форма – это форма представления, при которой информация преподнесена в виде фиксированного набора отдельных значений. То есть, например, последовательностью нулей и единиц. В свою очередь, дискретные устройства – это устройства, которые обрабатывают дискретные значения (сигналы).
В свою очередь, логический элемент – это дискретный преобразователь, который выдаёт после обработки двоичных сигналов значение одной из логических операций.
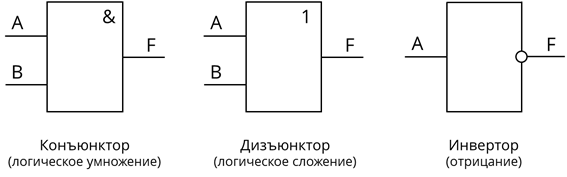
Перед вами представлены условные обозначения (схемы) логических элементов, с помощью которых реализуется логическое умножение, логическое сложение и отрицание. Давайте разберёмся с каждой схемой отдельно.
Итак, первый логический элемент И (конъюнктор). С его помощью реализуется операция логического умножения. Рассмотрим его.
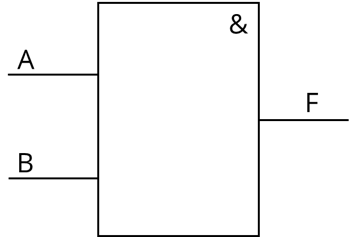
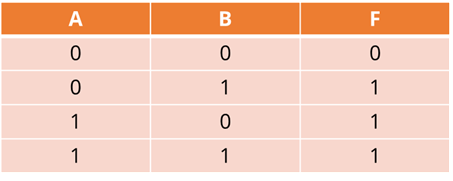
А – это входные данные первого элемента, B – второго, F – выходные данные. Вспомним таблицу истинности для конъюнкции.
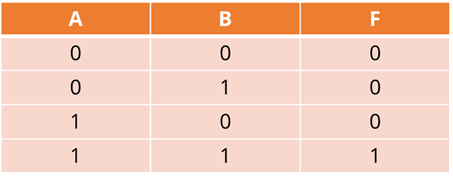
Всевозможные входные данные А и B нам даны в первых двух столбцах. В третьем нам дан результат при выполнении конъюнкции – выходные данные. То есть значение F. Таким образом, можно сказать, что единица на выходе получится тогда и только тогда, когда на всех входах будут единицы. Или же, другими словами, в результате мы можем получить для F единицу тогда и только тогда, когда А и B равны единице.
Следующий логический элемент – ИЛИ (дизъюнктор).
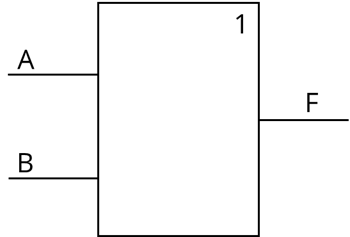
Как вы уже, наверное, догадались, с его помощью реализуется операция логического сложения. И снова обратимся к таблице истинности для дизъюнкции.
В первых двух столбцах даны всевозможные входные данные для А и B. В третьем выходные данные, которые будут равны F. Исходя из этой таблицы можно сказать, что на выходе мы получим единицу тогда, когда хотя бы на одном входе будет единица. То есть, если А или B будет равно единице, то F также будет равно единице.
И последний логический элемент – НЕ (инвертор).
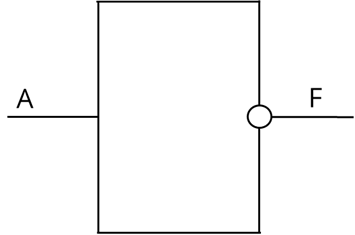
С его помощью реализуется операция отрицания.

Здесь всё просто. Снова нам понадобится таблица истинности для инверсии. Если на входе у нас элемент ноль, то на выходе будет единица, и наоборот. То есть, если А = 0, то F будет равно 1. И, если А = 1, то F = 0.
Также необходимо знать, что все компьютерные устройства, которые производят операции над двоичными числами, и ячейки, в которых хранятся данные, представляют собой электронные схемы. Они же в свою очередь состоят из отдельных логических операций.
А сейчас давайте попробуем проанализировать несколько электронных схем и узнать, какой сигнал получится на выходе.
Смотрим на первую схему.
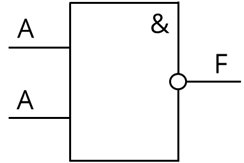
В ней используется только один элемент А. Снова будем использовать таблицу истинности. В первый столбец внесём входные данные ноль и один. Во второй столбец будем вносить данные, которые получаются при конъюнкции, в третьей – при инверсии. Он же будет являться столбцом, который будет обозначать выходные данные.

Мы видим, что от А идут две прямые. Это говорит о том, что одни и те же данные будут идти в двух направлениях. Первая операция – конъюнкция. При конъюнкции получим те же данные, что и в самом начале.
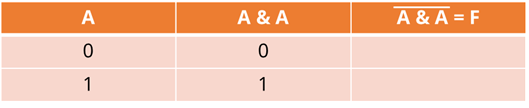
Далее идёт операция отрицания. При исходных данных, равных нулю получаем единицу, и наоборот, при исходных данных, равных единице получаем ноль.

Таким образом в итоге мы получили Ā. То есть можно сказать, что F = Ā.
Рассмотрим ещё одну схему.
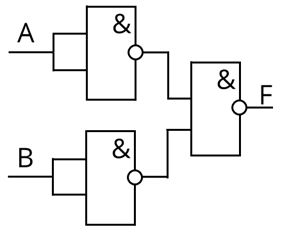
Она немного сложнее
первой. Снова будем использовать таблицу истинности. Она будет состоять из 8
столбцов. В первых двух будут находится входные данные А и B.
В третьем конъюнкция А, в четвёртом – конъюнкция B.
В пятые и шестые столбцы запишем отрицания конъюнкций А и B
соответственно. Для упрощения отрицания конъюнкций А и B
запишем как Ā и ![]() .
В седьмом будет находится конъюнкция Ā и
.
В седьмом будет находится конъюнкция Ā и ![]() .
И в последнем отрицание конъюнкции Ā и
.
И в последнем отрицание конъюнкции Ā и ![]() .
.

Таким образом мы с вами переписали все операции со схемы в таблицу истинности. Нам осталось только заполнить таблицу соответствующими данными. Итак, при конъюнкции двух А мы получим такие же данные как и в первом столбце. Перепишем их.

Аналогично поступим и с конъюнкцией двух B. Только данные будем брать со второго столбца.

Пятый столбец – Ā. Преобразуем данные, находящиеся в третьем столбце. Необходимо помнить, что при исходных данных, равных нулю, мы получим единицу. А при исходных данных, равных единице, получим ноль.

Аналогично и с шестым столбцом, а данные будем брать с четвёртого.
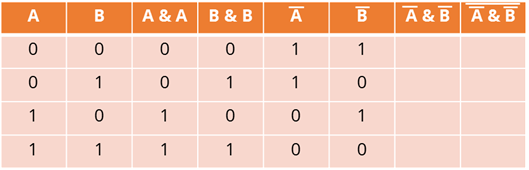
Седьмой столбец – это
конъюнкция Ā и ![]() .
Данные будем брать из пятого и шестого столбцов. Мы с вами помним, что на выходе
получим единицу тогда и только тогда, когда на всех входах будут единицы.
Заполним таблицу.
.
Данные будем брать из пятого и шестого столбцов. Мы с вами помним, что на выходе
получим единицу тогда и только тогда, когда на всех входах будут единицы.
Заполним таблицу.
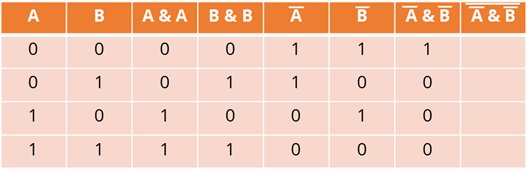
И последняя операция –
отрицание конъюнкции Ā и ![]() .
Исходные данные будем брать из седьмого столбца. И снова нужно знать, что если
исходные данные равны нулю, то на выходе мы получим один, и наоборот, если
исходные данные равны единице, то на выходе получим ноль.
.
Исходные данные будем брать из седьмого столбца. И снова нужно знать, что если
исходные данные равны нулю, то на выходе мы получим один, и наоборот, если
исходные данные равны единице, то на выходе получим ноль.
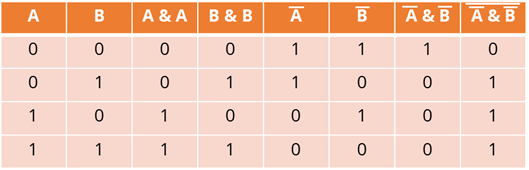
Таким образом мы с вами узнали, какие получатся выходные данные в нашей схеме. То есть данные из восьмого и есть наша F.
Если мы построим выражение исходя из таблицы истинности, то получим следующее:

И снова рассмотрим схему, но более простую.
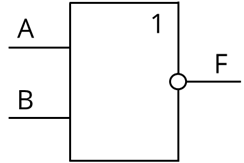
Для начала составим логическое выражение. Будем идти справа налево. Последний логических элемент, который к нас изображён – это инвертор. В него поступают сигналы от дизъюнктора. В свою очередь в дизъюнктор поступают данные от входа А и входа Бэ. В результате мы получим следующее:
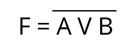
А сейчас давайте на основании этого логического выражения составим таблицу истинности и узнаем, какие данные получатся на выходе.
Таблица будет состоять из 4 столбцов. В первые два вносим исходные данные А и B соответственно. Далее мы будем выполнять дизъюнкцию, а затем инверсию. Это и будет являться заголовками наших столбцов.

Итак, первая операция – дизъюнкция. Мы с вами знаем, что на выходе мы получим единицу тогда, когда хотя бы на одном входе будет единица. Данные будем брать из первого и второго столбцов. Заполним третий столбец.
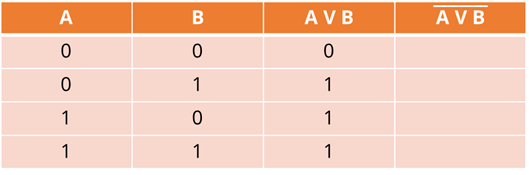
Для того, чтобы внести данные в четвёртый столбец, нам нужно брать входные данные из третьего. Если у нас входные данные равны нулю, то на выходе мы получим единицу, а если входные данные равны единицы, то на выходе будет ноль. Снова заполним таблицу.
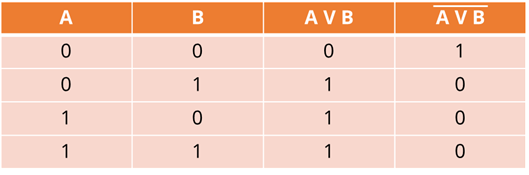
В четвёртом столбце находятся выходные данные для нашего выражения F.
А сейчас давайте рассмотрим пример, в котором мы сами научимся строить электронную схему исходя из логического выражения. А также найдём выходные данные с помощью таблицы истинности.
Итак, наше выражение выглядит следующим образом:
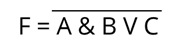
Сначала будет выполняться конъюнкция А и B. Изобразим А и B.

От них проведём две прямых и нарисуем прямоугольник, который будет обозначать конъюнктор. Поставим внутри соответствующий знак.

Далее у нас идёт дизъюнкция конъюнкции А и B с C. Изобразим C.
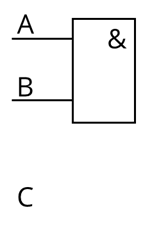
Затем проведём от неё ломанную. От конъюнктора также проведём прямую. И снова нарисуем прямоугольник, который будет изображать дизъюнктор. Снова поставим внутри соответствующий знак.
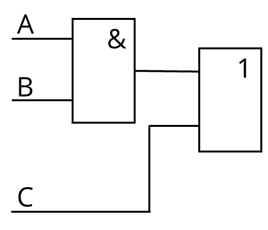
Нам осталось изобразить инвертор. Проведём от правой стороны дизъюнктора прямую и на пересечении дизъюнктора и прямой нарисуем незакрашенный кружок. Над выходной прямой напишем букву F.

Мы построили электронную схему. Теперь осталось построить таблицу истинности и найти выходные данные.
Таблица будет состоять из 6 столбцов. В первых трёх запишем всевозможные входные данные для А, B и C.
Четвёртый столбец – конъюнкция А и B, пятый дизъюнкция конъюнкции А и B и переменной C. Шестой инверсия всего выражения.

Теперь осталось заполнить таблицу данными.
При конъюнкции на выходе единица будет тогда и только тогда, когда на всех входах будут единицы. Для заполнения четвёртого столбца будем брать данные из первого и второго. Внесём данные в соответствии с данными.
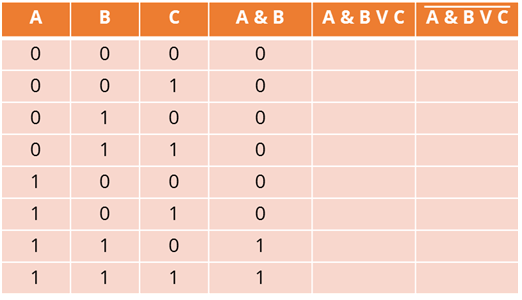
Пятый столбец – дизъюнкция. Данные будем брать из третьего и четвёртого столбцов. Заполним столбец в соответствии с правилом: на выходе будет единица тогда, когда хотя бы на одном входе будет единица.

И последний, шестой столбец – инверсия. Данные будем брать из пятого столбца. Если на входе у нас элемент ноль, то на выходе будет единица, и наоборот. Заполним столбец.
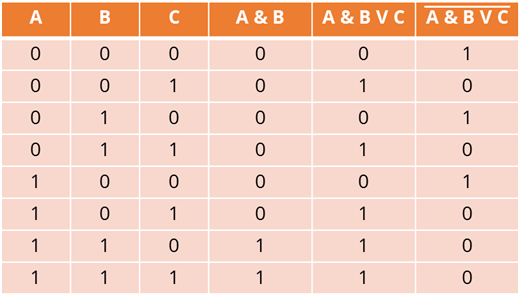
Данные этого столбца являются выходными данными построенной нами электронной схемы.
А теперь давайте исходя из таблицы истинности составим выражение, а исходя из выражения – построим электронную схему.

Нам дана таблица истинности, в которой записаны входные данные и операции, которые необходимо выполнить. Все операции указаны в порядке выполнения их в выражении. Для начала давайте заполним таблицу и найдём выходные данные.
Первая операция – дизъюнкция А и B. На выходе будет единица тогда, когда хотя бы на одном входе будет единица. Заполним четвёртый столбец исходя из данных первого и второго столбцов.
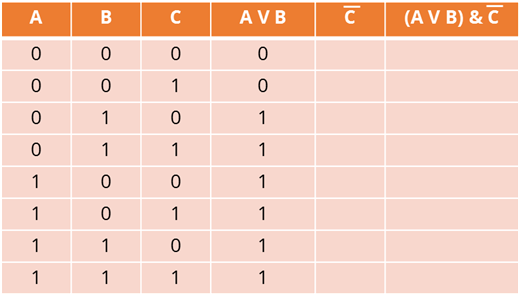
Вторая операция – инверсия C. Заполним пятый столбец исходя из данных третьего столбца. Необходимо помнить, что если входные данные равны нулю, то на выходе мы получим единицу. А если входные данные равны единице, то на выходе мы получим ноль. Внесём данные.
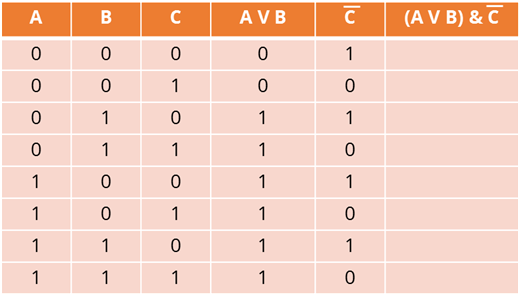
И последний столбец – конъюнкция дизъюнкции А или B и инверсии C. При выполнении конъюнкции мы с вами знаем, что на выходе единица будет тогда и только тогда, когда все входные данные равны единице. Заполним шестой столбец исходя из данных третьего и четвёртого столбцов.

Можно заметить, что всё наше выражение записано в шапке последнего шестого столбца. То есть, мы получим следующее:
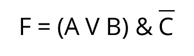
Нам осталось построить электронную схему.
Запишем А и B и проведём от них прямые к прямоугольнику, который будет обозначать дизъюнктор. Обозначим это соответствующим символом.
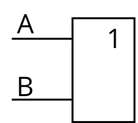
Теперь нам нужно изобразить инвертор. Для этого от C идут ломанные к конъюнктору. А на пересечение прямой, которая выходит из конъюнктора изобразим кружок, который и будет изображать отрицание.

Теперь проводим кривые от дизъюнктора и конъюнктора к новому прямоугольнику. Он будет изображать конъюнктор. Обозначим его соответствующим знаком.

Проводим прямую из правой стороны крайнего конъюнктора, которая будет обозначать выходные данные. Обозначим её буквой F.

Мы выполнили с вами задание, в котором записали выражение исходя из таблицы истинности и построили электронную схему.
А сейчас пришла пора подвести итоги урока.
Сегодня мы с вами познакомились с такими логическими элементами, как конъюнктор, дизъюнктор и инвертор.
Научились исходя из схемы при помощи таблицы истинности определять, какие данные должны получиться на выходе, а также научились строить электронные схемы по данному выражению и таблице истинности.

 Получите свидетельство
Получите свидетельство Вход
Вход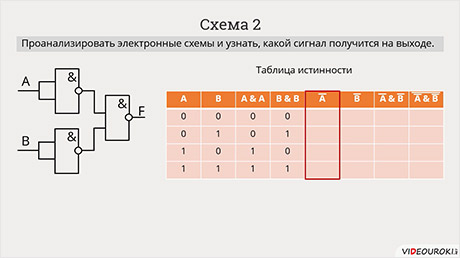




 18717
18717

