Построение таблиц истинности для логических выражений. Свойства логических операций

Сегодня мы узнаем, какие существуют правила для построения таблицы истинности для логических выражений, в которых количество логических операций больше одной. Также познакомимся со свойствами логических операций.

Прежде всего давайте вспомним логические операции, которые мы с вами изучали на прошлом уроке. К ним относятся инверсия, конъюнкция и дизъюнкция. Рассмотрите внимательно таблицу с обозначениями логических операций, которые мы будем использовать в дальнейшем.

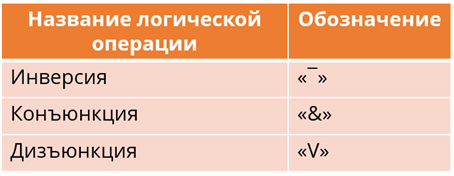
Конъюнкция – это логическая операция, которая объединяет два высказывания в одно новое, которое будет являться истинным тогда и только тогда, когда оба исходных высказывания истинны.

Дизъюнкция – это логическая операция, которая объединяет два высказывания в одно новое, которое будет являться ложным тогда и только тогда, когда ложны оба исходных высказывания.

Инверсия – это логическая операция, которая преобразует исходное высказывание в новое, значение которого противоположно исходному.

Логические выражения могут состоять из более чем двух логических операций. В тоже время, для любых логических выражений можно построить таблицу истинности, в которой мы сможем увидеть, какие значения принимает выражение. Логические операции выполняются в следующем порядке: инверсия, конъюнкция и дизъюнкция.

Итак, для начала рассмотрим, какие действия следует выполнить для построения таблицы истинности:

1. Подсчитать n – число переменных в выражении.

(А V B) & C.

Мы с вами знаем, что переменные обозначаются с помощью букв латинского алфавита.

n = 3.

2. Подсчитать общее число логических операций в выражении.

Количество логических операций: 2

То есть нам нужно сосчитать сколько в нашем выражении инверсий, конъюнкций и дизъюнкций.

3. Установить последовательность выполнения логических операций с учётом скобок и приоритетов. Как мы с вами знаем, сначала выполняются операции в скобках, затем инверсия, конъюнкция и дизъюнкция.

4. Определить число столбцов в таблице: число переменных плюс число операций. То есть нам нужно сложить количество переменных и логических операций. Мы получим число столбцов в таблице.

3 + 2 =5.

Количество столбцов: 5.

5. Заполнить шапку таблицы, включив в неё переменные и операции в соответствии с последовательностью, установленной в пункте три. То есть мы сначала пишем в шапке таблицы все наши переменные. Затем операции в порядке их следования.

6. Определить число строк в таблице (не считая шапки таблицы):

m = 2ⁿ.

m – это количество строк. n – число переменных в выражении. То есть, если наше логическое выражение будет состоять, например, из трёх переменных, то количество строк m = 2³ = 8. Шапка не входит в количество этих строк.

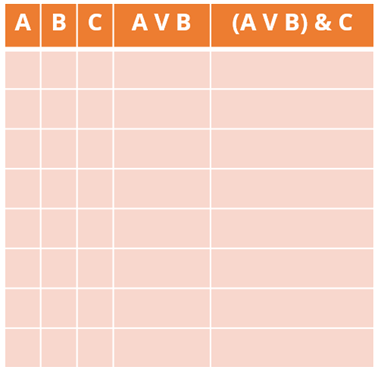
7. Выписать наборы входных переменных с учётом того, что они представляют собой ряд целых n-разрядных двоичных чисел от 0 до 2ⁿ – 1. Здесь мы должны написать все возможные входные переменные, как мы делали при построении таблиц истинности.

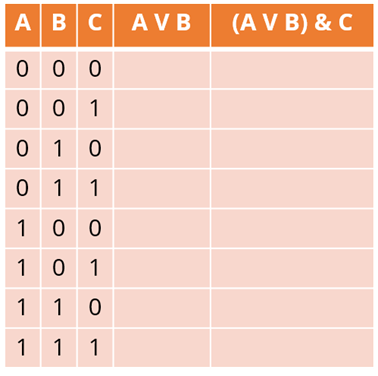
8. Провести заполнение таблицы по столбцам, выполняя логические операции в соответствии с установленной последовательностью. То есть произвести логические операции с входными данными в зависимости от логической операции.

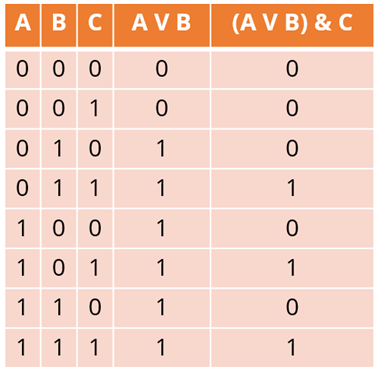
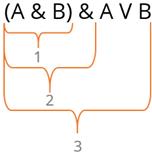
А теперь давайте разберёмся на примере. Необходимо построить таблицу истинности для следующего логического выражения: (A & B) & A V B.

Исходя из первого пункта плана построения таблицы истинности, нам нужно посчитать число переменных в выражении. Их у нас две: n = 2. А и B.

Общее число логических операций 3.

А сейчас давайте установим последовательность выполнения логических операций. Сначала будут выполняться логическая операция в скобках – конъюнкция. То есть первым будет выполнятся действие А & B.

Вторая логическая операция снова конъюнкция. И третья логическая операция – дизъюнкция.

Так как у нас 2 переменных и 3 логических операции, значит столбцов у нас будет 5. Так как в четвёртом пункте указан именно такой способ подсчёта столбцов.

Заполним теперь шапку таблицы. Сначала будут идти переменные А и B. Затем логические операции в порядке их выполнения.

Определимся с количеством строк. Нам дана формула для вычисления строк:

m = 2ⁿ.

n = 2.

m = 2² = 4.

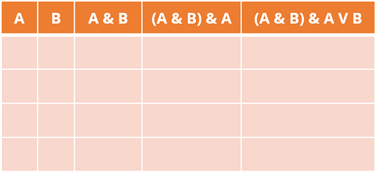
Теперь необходимо выписать наборы входных данных. То есть заполнить два первых столбца.

2² – 1= 4 – 1 = 3

Нам необходимо заполнить столбцы числами от 0 до 3. Так как все операции мы производим в двоичной системе счисления, то представим числа от 0 до 3 в двухразрядном двоичном коде. Получим следующие числа:

0₁₀ = 00₂

1₁₀ = 01₂

2₁₀ = 10₂

3₁₀ = 11₂

Теперь занесём эти числа в первый и второй столбцы. По одной цифре в ячейку.

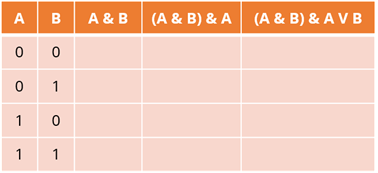
А сейчас заполним все остальные столбцы. Первая операция – конъюнкция. Данные будем вносить в третий столбец. Прежде, чем начать заполнение таблицы истинности вспомним правило для конъюнкции: новое высказывание будет истинно тогда и только тогда, когда исходные высказывания истинны. Значит в четвёртой строке для данного столбца будет стоять 1, так как это единственный случай, когда истинны оба исходных высказывания, значит и новое будет истинно. В первых трёх строках этого же столбца будут стоять нули, так как в первой строке ложны оба высказывания, во второй – высказывание А, а в третьей – высказывание B.

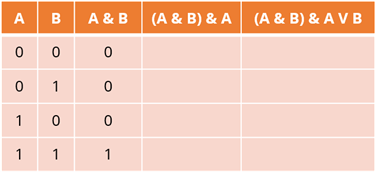
Переходим к четвёртому столбцу. Здесь снова логическая операция – конъюнкция. А данные мы будем брать из первого и третьего столбцов. И снова 1 будет стоять только в четвёртой строке для данного столбца, так как оба наших высказывания – истинны. В остальных – будут стоять нули.

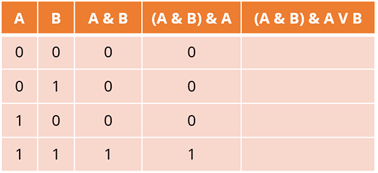
Нам осталось заполнить последний, пятый столбец. Логическая операция – дизъюнкция. Правило звучит следующим образом: новое высказывание будет ложно тогда и только тогда, когда ложны исходные высказывания. Рассматривать будем второй и четвёртый столбцы. Значит в первой и третьей строках для данного столбца будут стоять нули, так как оба выражения в данной ситуации ложны. В остальных строках этого же столбца будут стоять единицы.

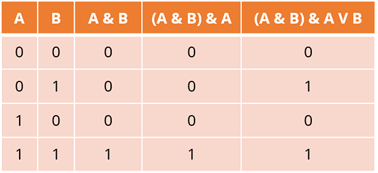
Мы построили таблицу истинности для нашего логического выражения. Следует обратить внимание, что данные в последнем столбце совпали с данными столбца B. В такой ситуации говорят, что логическое выражение (A & B) & A V B равносильно логической переменной B.

А сейчас рассмотрим основные свойства логических операций. Их называют законами алгебры логики.

1. Переместительный (коммутативный) закон: при перестановки местами переменных в конъюнкции и дизъюнкции значение выражения не изменяется.

A & B = B & A.

A V B = B V A.

Как мы знаем, конъюнкцию называет логическим умножением, а дизъюнкцию – логическим сложением. Если наши логические операции заменить соответствующими им арифметическими знаками, то мы можем видеть, что при перестановке местами переменных в умножении и сложении, значение выражения не изменяется.

A · B = B · A.

A + B = B + A.

2. Сочетательный (ассоциативный) закон: если в выражении все операции одинаковы, например, две конъюнкции, то скобки можно ставить произвольно или вообще опускать.

(A & B) & C = A & (B & C).

(A V B) V C = A V (B V C).

И снова если заменить логические операции соответствующими арифметическими знаками, то мы можем увидеть, где бы не стояли скобки, значение от этого не изменится, даже если скобки вообще будут отсутствовать.

(A · B) · C = A · (B · C);                            (A · B) · C = A · B · C.

(A + B) + C = A + (B + C);                       (A + B) + C = A + B + C.

3. Распределительный (дистрибутивный) закон.

A & (B V C) = (A & B) V (A & C)

A V (B & C) = (A V B) & (A V C)

И снова давайте заменим логические операции арифметическими знаками. Рассмотрим сначала логическое умножение. Получим:

A · (B + C) = (A · B) + (A · C).

A + (B · C) = (A + B) · (A + C).

Всё также, как и в алгебре.

4. Закон двойного отрицания: двойное отрицание исключает отрицание.

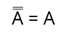
Если же говорить математическим языком, то можно сказать, что минус на минус даёт плюс.

– (– A) = A.

5. Закон исключённого третьего.

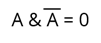
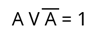
Рассмотрим логическое умножение.

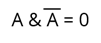
То есть если А = 0, то Ā = 1.

0 · 1 = 0.

И наоборот, если А = 1, то Ā = 0.

1 · 0 = 0.

Перейдём к логическому сложению.

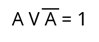
Если А = 0, то Ā = 1.

0 + 1 = 1.

И наоборот, если А = 1, то Ā = 0.

1 + 0 = 1.

Из этого можно сделать вывод: из двух противоречивых высказываний об одном и том же предмете одно всегда истинно, а второе – ложно, третьего не дано.

6. Закон повторения: при конъюнкции или дизъюнкции одного и того же высказывания, получится это же высказывание.

A & A = А.

A V A = А.

То есть:

A · A = А;

A + A = А.

Давайте рассмотрим логическое умножение. Например, если А = 0, то:

0 · 0 = 0.

А если А = 1, то:

1 · 1 = 1

При логическом сложении, если А = 0, то:

0 + 0 =0.

Если же А = 1, то:

1 + 1 =1.

Алгебра логики оперирует только двумя значениями: ложью (логический ноль) и истинной (логическая единица). Истина не может быть двойной, тройной или истиной в квадрате, поэтому при сложении двух истин результатом будет просто истина, то есть цифра 1.

7. Законы операций с 0 и 1.

Здесь всё просто. Рассмотрим конъюнкцию.

При умножении любого выражения на 0 мы всегда получим 0, а при умножении любого выражения на 1 – всегда будем получать это же выражение.

A & 0 = 0;           A · 0 = 0.

A & 1 = A;          A · 1 = А.

А если же рассматривать дизъюнкцию, то при прибавлении к выражению 0 мы получим это же выражение. А вот при прибавлении к выражению 1, в результате получим 1. Почему мы получаем именно единицу, мы уже рассматривали с вами на примере прошлого закона.

A V 0 = А;          A + 0 = A.

A V 1 = 1;           A + 1 = 1.

8. Закон общей инверсии. Для того, чтобы найти инверсию конъюнкции, нужно найти дизъюнкцию инверсий каждого логического выражения. Для того, чтобы найти инверсию дизъюнкции, нужно найти конъюнкцию инверсий каждого логического выражения.

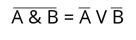
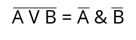
Все законы алгебры логики можно доказать с помощью таблиц истинности.

Давайте докажем закон общей инверсии для логического умножения.

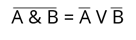
Построим таблицу. У нас 2 переменных в выражении. Число логических операций равно 5. Значит число столбцов будет равно 7.

Теперь установим последовательность выполнения логических операций. Для начала будем брать выражение слева от равно. Значит в первую очередь будет выполняться конъюнкция, а затем инверсия.

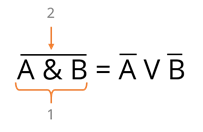
Справа от равно будет сначала выполняться инверсия А, затем инверсия B и после этого – дизъюнкция получившихся выражений.

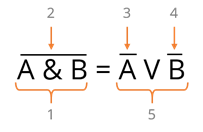
Зададим названия для наших столбцов в соответствии с порядком выполнения операций.

Количество строк будет равно 4 (шапка таблицы сюда не входит), так как:

2² = 4.

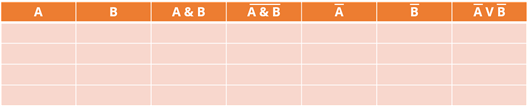
Теперь выпишем наборы входных переменных. Это будут числа от 0 до 3. Представим их в двухразрядном коде и получим следующие числа:

0₁₀ = 00₂

1₁₀ = 01₂

2₁₀ = 10₂

3₁₀ = 11₂

Заполним таблицу.

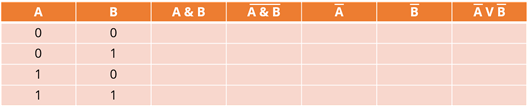
Теперь перейдём непосредственно к логическим операциям. Первая – конъюнкция А и B. Новое высказывание будет истинно тогда и только тогда, когда истинны исходные высказывания. Значит единица будет стоять в последней строке для данного столбца, а во всех остальных – нули.

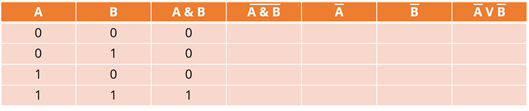
Следующая операция – инверсия. Если исходное высказывание было истинно, то после инверсии оно становится ложным, а если исходное высказывание было ложным, то после операции инверсии оно становится истинным. Значит если у нас единица, то она будет заменена на ноль, а если ноль, то на единицу. Заполним четвёртый столбец, исходя из данных, которые находятся в третьем столбце.

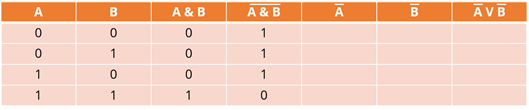
Мы получили результат выражения, которое находится слева от равно. Обведём наш столбец. Он нам понадобится в дальнейшем.

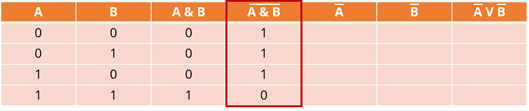
Идём дальше. Пятый столбец – инверсия А. И снова, если исходное выражение равно единице, то оно станет равно нулю и наоборот. Заполним столбец цифрами, исходя из данных, которые находятся в первом.

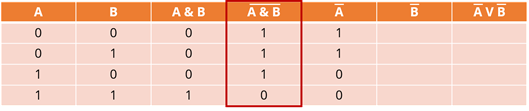
Аналогично заполним шестой столбец. Только опираться мы будем на второй.

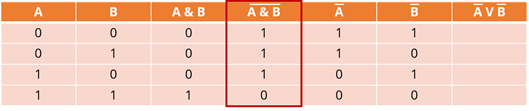
Последняя операция – дизъюнкция. Новое высказывание будет ложно тогда и только тогда, когда ложны исходные высказывания. Значит 0 будет стоять в последней строке для данного столбца, а во всех остальных – единицы.

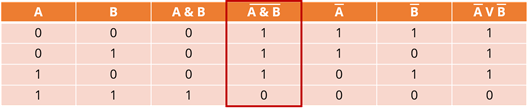
Мы получили результат выражения, которое стоит справа от равно. Также обведём его.

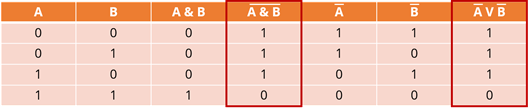
Давайте посмотрим на выделенные столбцы. Их значения совпадают. Это и доказывает справедливость закона общей инверсии.

Давайте найдём значение логического выражения: (D > 1) V (D < 2). Число D = 1.

Переходим к решению. D = 1 получим следующее:

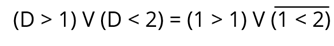
Логическое выражение «1 > 1» не верно. Заменим его 0. Выражение «1 < 2» – верно, поэтому заменим его 1. Получим:

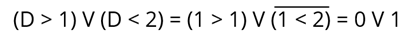
И это будет равно:

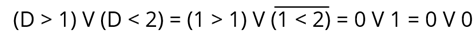
Вернёмся к закону повторения. Согласно этому закону, значение данного логического выражения равно нулю. Таким образом значение нашего логического выражения, при D = 1, равно 0.

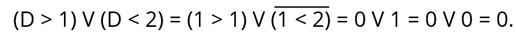
А сейчас подведём итоги нашего урока. Сегодня мы познакомились с правилами построения таблиц истинности для логического выражения. Научились строить таблицу истинности для логического выражения на примере. Также узнали, какие существуют законы алгебры логики и с помощью таблицы истинности доказали достоверность одного из них.