Задача 1. В каких пропорциях нужно смешать а%-й и b%-й растворы кислоты (a b), чтобы получить с%-й раствор?
Возьмем х г а%-го раствора и у г b%-го раствора кислоты. Составим таблицу:
| Kонцентрация раствора, | Масса раствора, | Масса кислоты, |
| a | х | 0,01ax |
| b | у | 0,01by |
| c (смесь) | x + y | 0,01c(x + y) |
Составим и решим уравнение:
0,01ах + 0,01by = 0,01c(x + y),
(b – с)у = (с – а)х,
x : у = (b – с) : (с – а).
Воспользуемся диагональной схемой*:
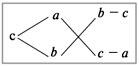
В этой схеме а и b – концентрации исходных растворов, с – требуемая концентрация кислоты в процентах, а «крест-накрест» – записаны их разности (b – с) и (с – а), соответствующие отношению масс растворов а и b.
Задача 2. Сколько по массе 90%-го и 60%-го растворов фосфорной кислоты надо взять, чтобы получить 5,4 кг 80%-го раствора фосфорной кислоты?
Решение
Составим диагональную схему:
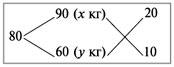
Получаем:
х : у = 20 : 10 = 2 : 1.
Значит, 90%-го раствора фосфорной кислоты надо взять в 2 раза больше, чем 60%-го, т.е. х = 2y.
Составим уравнение: 2y + y = 5,4.
Отсюда y = 1,8 кг.
Ответ. 3,6 кг 90%-го и 1,8 кг 60%-го
растворов фосфорной кислоты.
Задача 3. Сплавили два слитка серебра: 75 г 600-й и 150 г 864-й пробы. Определить пробу сплава.
Решение
Пусть проба сплава равна х.
Составим диагональную схему:
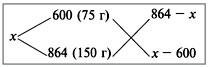
Получаем:
(864 – х) : (х – 600) = 75 : 150 = 1 : 2;
1728 – 2х = х – 600; х = 776.
Ответ. Получили сплав 776-й пробы.
Задача 4. Смешали некоторые количества 72%-го и 58%-го растворов кислоты, в результате получили 62%-й раствор той же кислоты. Если бы каждого раствора было взято на 15 л больше, то получился бы 63,25%-й раствор. Сколько литров каждого раствора было взято первоначально для составления первой смеси?
Решение
Дважды используем диагональную схему:
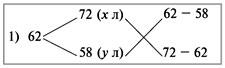
Получаем:
х : у = 4 : 10 = 2 : 5.
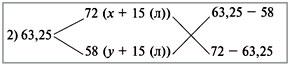
Получаем:
(х + 15) : (y + 15) = 5,25 : 8,75 = 3 : 5.
Составим систему уравнений и решим ее:
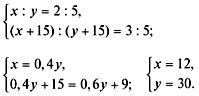
Ответ. В первой смеси было 12 л 72%-го раствора
и 30 л 58%-го раствора.
Задача 5. Сколько граммов 9%-го раствора спирта можно получить из 200 г 70%-го раствора спирта?
Решение
9%-й раствор спирта получают из 70%-го, разбавляя его водой. В воде 0% спирта. Применим диагональную схему:
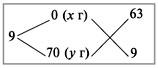
Получаем:
х : у = 63 : 9 = 7 : 1.
Значит, 1 часть 70%-го раствора спирта надо разбавить 7 частями воды. Поэтому 200 г 70%-го раствора спирта надо разбавить 200•7 = 1400 г воды.
Всего получим: 200 + 1400 = 1600 г 9%-го раствора спирта.
Ответ. Из 200 г 70%-го раствора спирта можно
получить 1 кг 600 г 9%-го раствора спирта.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Задачи на смеси и сплавы (47.46 KB)
Задачи на смеси и сплавы (47.46 KB)
 0
0 872
872 14
14 Нравится
0
Нравится
0







