Текстовые алгебраические задачи представляют собой традиционный раздел элементарной математики. Интерес к нему вполне понятен. Решение задач подобного рода способствует развитию логического мышления, сообразительности и наблюдательности, умения самостоятельно осуществлять небольшие исследования. Рассмотрим задачи, решение которых связано с понятиями «концентрация», «процентное содержание». В условиях таких задач речь идет, чаще всего, о сплавлении каких-либо металлов, растворении друг в друге различных веществ или переливании жидкостей, состоящих из нескольких компонентов. У многих учащихся эти задачи вызывают затруднения. Вероятно, это связано с тем, что таким задачам в школьном курсе математики уделяется совсем мало времени. Вместе с тем они входят в различные сборники заданий по подготовке к итоговой аттестации по математике за курс основной школы, включаются в варианты ЕГЭ и вступительных экзаменов в ВУЗы.
Основные допущения, принимаемые в задачах подобного рода, состоят в следующем:
а) все получающиеся смеси и сплавы однородны;
б) при слиянии двух растворов, имеющих объемы V1 и V2, получается смесь, объем которой равен V1+ V2, т. е. V0= V1+ V2, причем последнее соотношение является именно допущением, поскольку не всегда выполняется в действительности; при слиянии двух растворов не объем, а масса смеси равняется сумме масс составляющих ее компонентов.
В задачах этого типа обычно присутствуют три величины, соотношение между которыми позволяет составить уравнение:
- концентрация (доля чистого вещества в сплаве / смеси);
- количество чистого вещества в смеси (сплаве);
- масса смеси (сплава).
Пусть в смесь входят компоненты A, B, C с массами mA, mB, mC. Будем считать, что масса смеси равна сумме масс компонент, т. е. m=mA+mB+mC. Тогда концентрацией компоненты A по массе называется отношение массы этой компоненты к массе всей смеси.

Сумма всех концентраций, очевидно, равна единице.
Объемным процентным содержанием компоненты A называется величина
PA= CA ·100%
т. е. это концентрация вещества, выраженная в процентах.
Если известно процентное содержание вещества A, то его концентрация находится по формуле
СА=РА/100, аналогично СВ=РВ/100, СС=РС/100,
Так, например, если процентное содержание составляет 70%, то соответствующая концентрация равна 0,7. О какой концентрации, объемной или массовой, идет речь в конкретной задаче, всегда ясно из ее условия.
Задачи.
При решении задач удобно пользоваться наглядной моделью-схемой, в которой смесь (раствор, сплав) изображается в виде прямоугольника, разбитого на фрагменты в соответствии с числом входящих в нее (в него) компонент, а непосредственно при составлении уравнения – проследить содержание какой-нибудь одной компоненты.
Пример 1. Имеются два куска сплава меди и цинка с процентным содержанием меди 42% и 65% соответственно. В каком отношении нужно взять эти сплавы, чтобы переплавив получить сплав, содержащий 50% меди ?
Решение. Пусть масса первого куска равна x г, а масса второго - y г. Составим схему.
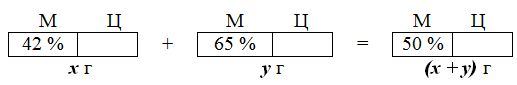
Зная, что сумма масс меди в исходных сплавах равна массе меди в новом сплаве, составим уравнение
0,42x+0.65y=0,5(x+y),
из которого x:y=15:6. Значит, нужно взять первый и второй сплавы в отношении 15:6.
Ответ. 15:6.
Пример 2. [1] К 40%-ному раствору соляной кислоты добавили 50 г чистой кислоты, после чего концентрация раствора стала равной 60%. Найдите первоначальную массу раствора.
Решение. Введем обозначения: К – соляная кислота, В – вода. Пусть x г – первоначальная масса раствора.

Составим уравнение на основе подсчета массы соляной кислоты
0,4x+50=0,6(x+50),
Откуда x = 100.Первоначальная масса раствора равна 100г.
Ответ. 100 г.
Пример 3. [1] Из 10 кг свежих фруктов получается 3,5 кг сушеных фруктов, содержащих 20% влаги. Чему равно процентное содержание влаги в свежих фруктах ?
Решение. Введем обозначения: СФ – сухофрукты, В – вода. Пусть в свежих фруктах содержится x % воды.

Составим уравнение на основе подсчета массы воды
0,1x-6,5=0,2·3,5,
Откуда x = 72.В свежих фруктах 72% воды.
Ответ. 72 %.
Пример 4. [3] Имеются два сплава, состоящие из цинка меди и олова. Известно, что первый сплав содержит 40% олова, а второй – 26% меди. Процентное содержание цинка в первом и во втором сплавах одинаково. Сплавив 150 кг первого сплава и 250 кг второго, получили сплав, в котором оказалось 30% цинка. Определить сколько килограммов олова содержится в получившемся сплаве.
Решение. Если процентное содержание цинка в первом и втором сплавах одинаково, то оно равно 30%. Составим схему. Воспользуемся следующими обозначениями: С – цинк, М – медь, О – олово.

Задачу можно решить без уравнения. Масса олова в получившемся сплаве равна 150 · 0,4 + 250 · 0,44 = 170 (кг)
Ответ. 170 кг.
Литература.
- Захарова А. Е. Учимся решать задачи на смеси и сплавы // Математика для школьников.-2006.-№3.-С.18-21.
- Лурье, М. В. Задачи на составление уравнений: Учеб. руководство / М. В. Лурье, Б. И. Александров. - 3-е изд., перераб. – М. Наука. Гл. ред. Физ.-мат. Лит., 1990-96с.
- Цыганов Ш. И. Все задачи ЕГЭ по математике прошлых лет: Учебное пособие / Ш. И. Цыганов – 4-е изд., дополненное – Уфа: Центр педагогических измерений, 2008-324с.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Задачи на смеси и сплавы (59 КB)
Задачи на смеси и сплавы (59 КB)
 1
1 1429
1429 186
186 Нравится
0
Нравится
0







