Урок математики в 7 классе
Тема: Задачи на растворы, смеси, сплавы.
Основные цели урока:
Образовательные.
Закрепить умения и навыки в решении задач на растворы, смеси, сплавы.
Развивающие.
Развитие интереса к предмету.
Познакомить учащихся с краткой биографией Д.И. Менделеева.
Активизация мыслительной деятельности.
Воспитательные.
Формирование навыков решения практических задач, используя математические знания.
Оборудование:
Формы работы:
Фронтальная, групповая, индивидуальная.
Ход урока
1. Мотивация к учебной деятельности:
1. Добрый день, ребята!
В 2014 году мы отмечаем две химически знаменательные даты: 180 лет со дня рождения Д. И. Менделеева (он родился 8 февраля 1834г.) и 145 лет со дня открытия его Периодического закона и Периодической системы химических элементов (1 марта 1869 года). (Слайд 1)
2. Сообщение учащихся:
Родился 27 января 1834 года, в городе Тобольск.
Выдающийся русский химик, наиболее известное его открытие — периодический закон химических элементов, в соответствии с которым составил периодическую систему элементов.
Автор фундаментальных исследований по химии, физике, метрологии, метеорологии, экономике, основополагающих трудов по воздухоплаванию, сельскому хозяйству, химической технологии, народному просвещению.
Умер — 20 января 1907 года, в городе Санкт-Петербург. (Слайд 2)
«Природа – мать
Когда б таких людей
Ты иногда не посылала миру,
Заглохла б нива жизни…»
Н. А. Некрасов.
«Сам удивляюсь, чего я только не делывал в своей научной жизни» - писал о себе Д.И.Менделеев. За всю свою жизнь он написал и опубликовал 431 работу.
Но его деятельность далеко выходила за рамки чистой науки химии. Русский химик Л.А.Чугаев (1873-1922) писал: «Гениальный химик, первоклассный физик, плодотворный исследователь в области гидродинамики, метеорологии, геологии, в различных отделах химических технологий (взрывчатые вещества, нефть, учение о топливе и др.) и других, сопредельных с химией и физикой дисциплинах. Глубокий знаток химической промышленности вообще, особенно русской, оригинальный мыслитель в области учения о народном хозяйстве, государственный ум, которому, к сожалению, не суждено было стать государственным человеком, но который видел и понимал задачи и будущность России лучше представителей нашей официальной власти».
А ученик Менделеева Г.Г.Густавсон (1842-1908) отмечал: «К какому бы делу он ни прикасался, он всегда оставлял на нем глубокие и поучительные следы».
3. Учитель:
Вся жизнь Д.И.Менделеева – служение на процветание России. Это пример того, как ученые могут и должны служить Родине.
Всем известны его Периодический закон и Периодическая система. 1 марта 1869г. считается днем рождения Периодического закона, а Периодическая система Д.И.Менделеева – это его графическое выражение.
Д. И. Менделеев – гениальный русский химик. (Слайд 3)
4. Учитель:
- В следующем учебном году в 8 классе вы тоже начнете изучать интересный предмет химию. Естественно, математика тесно связана с физикой и химией.
«Химия – правая рука физики, математика ее глаз». (М.В. Ломоносов) (Слайд 4)
- Сегодня на уроке мы немного погрузимся в мир химии. Я предлагаю вам поработать над задачами на растворы, смеси и сплавы.
Учащиеся записывают в тетради дату, тему урока.
- Какова цель урока? (Потренироваться в решении задач на растворы, смеси, сплавы) (Слайд 5)
2. Актуализация опорных знаний обучаемых
- Ребята, ответьте, пожалуйста, на вопросы.
Зачем решать задачи на смеси?
Предполагаемые ответы учащихся:
В обыденной жизни, мы сможем применить свои знания по решению подобных задач, разбавляя уксусную эссенцию для домашних заготовок, готовя растворы для полива почв на садовом участке, рассчитывая массу драгоценных металлов в ювелирных украшениях.
Организация здорового образа жизни заставляет нас чаще заглядывать на упаковки продуктов питания, чтобы увидеть процентное содержание различных веществ. Мы говорим об экологии района, когда видим объемную долю газообразных выбросов предприятий и транспорта.
Что такое смесь, и какие бывают смеси?
Предполагаемые ответы учащихся:
Смесь – это система, состоящая из двух и более компонентов.
Смеси бывают: жидкие, твердые, газообразные.
Смеси бывают: однородные и неоднородные. (Слайд 6)
Где мы встречаем смеси?
Предполагаемые ответы учащихся:
Смеси окружают нас повсюду:
атмосфера (воздух);
гидросфера (вода),
литосфера (горные породы);
смеси есть в биосистемах, в продуктах производимых человеком (растворах, сплавах).
Совершенно верно, ребята! Итак, задачи подобного плана мы встречаем в различных ситуациях:
смешение жидкостей с различным содержанием соли;
смешение кислот разной концентрации;
сплавление металлов с разным содержанием некоторого металла. (Слайд 7)
Далее с помощью справочной литературы учащиеся знакомятся с основными теоретическими сведениями по данной теме. При этом учащиеся составляют опорный конспект (используют Приложение 1).
(Слайд 8, Слайд 9)
3. Решение задач
А сейчас я предлагаю поработать в группах и решить задачи. После работы в группах обсуждается решение, и составляются алгоритмы решения задач.
Задача 1
Даны два куска с различным содержанием олова. Первый, массой 300г, содержит 20% олова. Второй, массой 200г, содержит 40% олова. Сколько процентов олова будет содержать сплав, полученный из этих кусков?
Решение.
1) 300 •20 : 100 = 60 (г) - олова в первом сплаве,
2) 200 • 40 : 100 = 80 (г) - олова во втором сплаве ;
3) 60 + 80 = 140 (г) - олова в двух сплавах вместе;
4) 200 + 300 = 500 (г) – масса куска после сплавления;
5) 140 : 500 • 100 = 28% -содержится олова после сплавления.
Ответ: 28 %. (Слайд 10)
Задача 2
Сколько литров воды надо добавить к 20 литрам 5% раствора соли, чтобы получить 4% раствор?
Решение.
Пусть количество добавленной воды – х (л),
тогда масса нового раствора – 20+х (л),
20×0,05=1(л)- содержится соли в 20 литрах 5% раствора.
Имеем : соли 1 (л) это 4%,
раствора 20+х (л) это 100%.
Составим и решим уравнение:
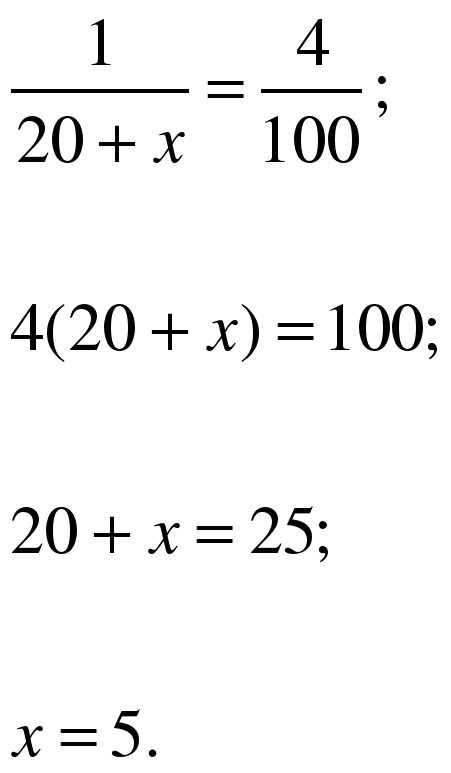 Ответ:
Ответ: 5 литров воды надо добавить. (
Слайд 13)
Алгоритм 1
Арифметический способ решения
При образовании смеси складываются компонентов смеси. Поэтому, если известны только процентные содержания, то нужно:
1) Посчитать количество компонентов каждой смеси (в граммах, литрах и т.д.)
2) Сложить количество компонентов полученной смеси;
3) Найти массу полученной смеси;
4) Подсчитать относительное (процентное) содержание компонентов полученной смеси;
5) Записать ответ. (Слайд 11)
Алгоритм 2
Применение линейного уравнения
При составлении уравнения прослеживается содержание какого-нибудь одного вещества из тех, которые сплавляются (смешиваются) и т.д.
1) Обозначить неизвестную величину через х;
2) Составить уравнение по условию задачи;
3) Решить получившееся уравнение;
4) Перейти к условию задачи (ответить на вопрос);
5) Записать ответ. (Слайд 14)
4. Самостоятельное решение задач
Смешали 300г 50%-го и 100г 30%-го раствора кислоты. Определите процентное содержание кислоты в полученной смеси.
(Из «Арифметики» А.П. Киселева) 30 ведер вина в 48 градусов смешано с 24 ведрами вина в 36 градусов. Сколько градусов в смеси? (Число градусов означает процентное содержание чистого спирта в вине)
Имеется чай двух сортов – по 80р. И 120р. За 1кг. Смешали 300г первого и 200 г второго сорта. Определите цену 100г полученной смеси.
У торговца имеется два бочонка вина: емкостью 40л и емкостью 10л. Цены вина за литр различны, но неизвестны. По какому одинаковому количеству вина надо взять из каждого бочонка и перелить в другой бочонок, чтобы цена вина за литр в двух бочонках сравнялась.
Имеется кусок сплава меди с оловом 12кг содержащий 45% меди. Сколько чистого олова надо прибавить к этому сплаву, чтобы получился новый сплав содержащий 40% меди? (Слайд 12, Слайд 15)
5. Подведение итогов урока
Учитель:
Какие умения вы сегодня тренировали?
Какие знания вы использовали при выполнении заданий?
Какие затруднения возникали в процессе работы над заданиями?
Вернемся к началу нашего урока. В 2014 году исполняется 180 лет со дня рождения Д.И. Менделеева. Его часто называли гением, но он этого не любил и, как правило, сердился: «Ну какой же я гений? Трудился всю жизнь, вот и стал гением».
Я желаю вам, ребята, чтобы вы трудились. Выпускник школы должен уметь решать расчетные задачи данного типа (на растворы, смеси, сплавы) и применять свои знания в дальнейшей жизни.
Наш урок подошел к концу. Было приятно с вами работать. Поблагодарите друг друга за плодотворное сотрудничество.
Выставление оценок.
Домашнее задание:
Составить самостоятельно и решить 2 задачи «на растворы, смеси, сплавы», используя жизненные ситуации.
Литература:
Лебедев В.В., Михайлов П.А., Ефимова М.В. Пособие по математике для подготовки к вступительному экзамену в Государственную академию управления. -М.:ГАУ,УЦ «АЗЪ»,1998.
Математика, № 6, 2006. (Приложение «1 сентября»).
Семёнова А.Л. ЕГЭ 2012. Математика. Типовые экзаменационные варианты. -М.: Национальное образование , 2011.
Шевкин А.В. Текстовые задачи. 7-11 классы: Учебное пособие по математике. –М.:Русское слово – РС,2005.
ПРИЛОЖЕНИЕ 1
«Задачи на растворы, смеси и сплавы»
Основными компонентами в этих задачах являются:
Масса раствора равна __________________________________________________________.
Масса сплава равна ____________________________________________________________.
Масса смеси равна ____________________________________________________________.
Концентрация или процентное содержание вещества – это ___________________________ __________________________________________________________________________.
Обозначения:
M – масса всего раствора (сплава)
m – масса растворенного вещества
k – концентрация раствора

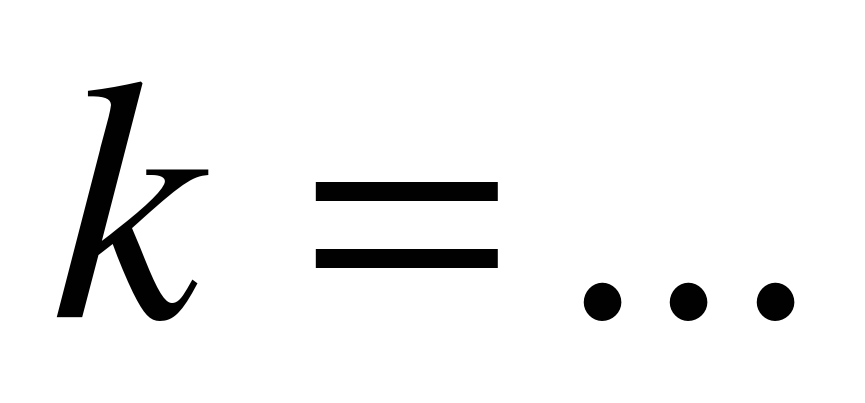
Алгоритм 1
Арифметический способ решения
При образовании смеси складываются компонентов смеси. Поэтому, если известны только процентные содержания, то нужно:
1) Посчитать количество компонентов каждой смеси (в граммах, литрах и т.д.)
2) _____________________________________________________;
3) Найти массу полученной смеси;
4) ________________________________________________________________________;
5) Записать ответ.
Алгоритм 2
Применение линейного уравнения
При составлении уравнения прослеживается содержание какого-нибудь одного вещества из тех, которые сплавляются (смешиваются) и т.д.
1) ___________________________________________;
2) Составить уравнение по условию задачи;
3) _______________________________________________;
4) Перейти к условию задачи (ответить на вопрос);
5) Записать ответ.
«Задачи на растворы, смеси и сплавы»
(образец заполненного конспекта)
Основными компонентами в этих задачах являются:
Масса раствора равна сумме масс воды и соли.
Масса сплава равна сумме масс металлов, входящих в этот сплав.
Масса смеси равна сумме масс компонентов этой смеси.
Концентрация или процентное содержание вещества – это отношение массы вещества к массе раствора (смеси, сплава), записанное в виде процентов.
Обозначения:
M – масса всего раствора (сплава)
m – масса растворенного вещества
k – концентрация раствора

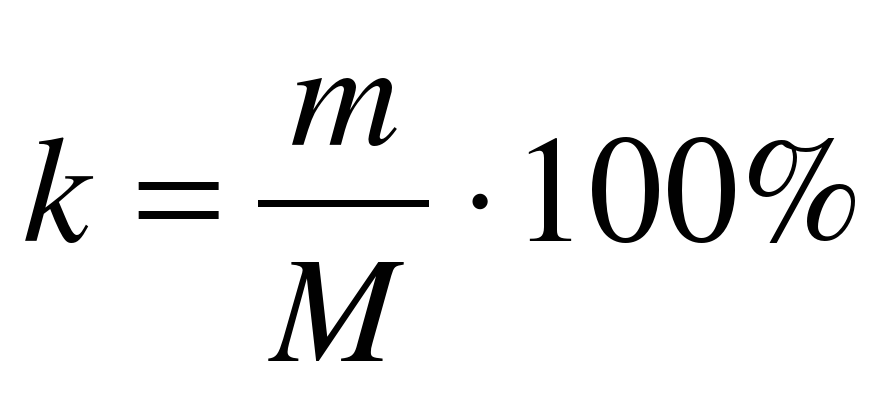
Алгоритм 1
Арифметический способ решения
При образовании смеси складываются компонентов смеси. Поэтому, если известны только процентные содержания, то нужно:
1) Посчитать количество компонентов каждой смеси (в граммах, литрах и т.д.)
2) Сложить количество компонентов полученной смеси;
3) Найти массу полученной смеси;
4) Подсчитать относительное (процентное) содержание компонентов полученной смеси;
5) Записать ответ.
Алгоритм 2
Применение линейного уравнения
При составлении уравнения прослеживается содержание какого-нибудь одного вещества из тех, которые сплавляются (смешиваются) и т.д.
1) Обозначить неизвестную величину через х;
2) Составить уравнение по условию задачи;
3) Решить получившееся уравнение;
4) Перейти к условию задачи (ответить на вопрос);
5) Записать ответ.


 Получите свидетельство
Получите свидетельство Вход
Вход



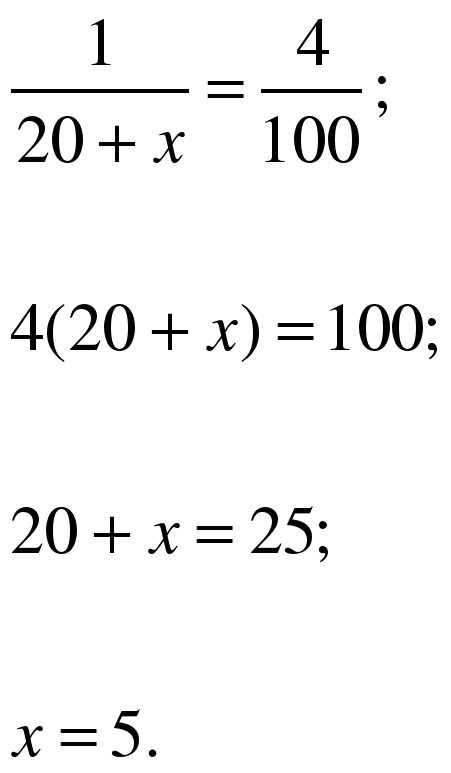 Ответ: 5 литров воды надо добавить. (Слайд 13)
Ответ: 5 литров воды надо добавить. (Слайд 13) 








 Сценарий урока по математике "Задачи на растворы, смеси, сплавы" (85 КB)
Сценарий урока по математике "Задачи на растворы, смеси, сплавы" (85 КB)
 0
0 1391
1391 88
88 Нравится
0
Нравится
0






