Республика Татарстан
Мамадышский муниципальный район
Муниципальное образовательное учреждение «Верхнесуньская СОШ»
Проектная работа
Тема: «Методика подготовки учащихся к решению задач по теме: задачи на смеси и сплавы, включенных в ЕГЭ по математике»
Хуснуллина Расима Габдулхаевна–
учитель математики
МБОУ «Верхнесуньская СОШ»
2015г.
Содержание
1. Введение…………………………………………………………………….3
2. Теоретические основы решения задач «на смеси, сплавы, растворы»…6
3. Различные способы решения задач………….…………………………….6
4. Задачи на понижение концентрации……………………………………..10
5. Задачи на высушивание…………………………………………………...11
6. Задачи на смешивание растворов разных концентраций……………….12
7. Задачи на повышение концентрации……………………………………..13
8. Задачи вариантов ЕГЭ……………………………………………………..14 9.Заключение………………………………………………………………….17
10. Использованная литература……………………………………………...18
Введение
«Развивающему обществу нужны современные образованные, нравственные, предприимчивые люди, которые могут самостоятельно принимать ответственные решения в ситуации выбора, прогнозируя их возможные последствия, способные к сотрудничеству, отличающиеся мобильностью, динамизмом, конструктивностью, обладающие развитым чувством ответственности за судьбу страны» (Концепция модернизации российского образования).
В связи с этим появились современные государственные образовательные стандарты общего образования, началось более широкое внедрение современных информационных технологий в преподавании всех школьных предметов, изменились цели обучения. Все это в равной мере касается и образовательной области «математика».
Доминирующей идеей федерального компонента государственного образовательного стандарта по математике является интенсивное развитие логического мышления, пространственного воображения, алгоритмической культуры, критического мышления, овладения математическими знаниями и умениями на всех ступенях обучения, использование приобретенных знаний и умений в практической деятельности.
Актуальность данной темы в настоящее время, объясняется тем, что в России модернизация касается и образования. Единый государственный экзамен должен не только определить уровень подготовки выпускников школ, но и задать направление развития школьной математики на ближайшие несколько лет.
Актуальность данной темы обусловлена ещё и тем, что единый государственный экзамен как форма аттестации перешла из экспериментального в штатный режим.
Цель проекта: использование педагогических технологий в учебном процессе с целью повышения качества знаний, умений и навыков.
Задачи проекта:
Повысить интерес и мотивацию учеников к изучению математики.
Развивать навыки самостоятельной деятельности учащихся.
Совершенствовать навыки работы с учебником.
Разработать методику для подготовки учащихся к ЕГЭ.
Методы исследования: анализ методической и учебной литературы, базы данных математических задач "Задания для подготовки к единому государственному экзамену" для учащихся 10, 11-х классов
Предполагаемые продукты
Конечный результат: успешная сдача ЕГЭ, возможность получить аттестат о среднем образовании учащихся.
Основная задача обучения математике в школе заключается в обеспечении прочного и сознательного овладения учащимися системой математических знаний и умений, необходимых в повседневной жизни и трудовой деятельности, достаточных для изучения смежных дисциплин и продолжения образования, в профессиональной деятельности, требующей достаточно высокой математической культуры. В процессе решения задач на смеси и сплавы в арсенал приемов и методов человеческого мышления включается индукция и дедукция, обобщение и конкретизация, анализ, классификация и систематизация, аналогия.
В школьном курсе математики мало времени уделяется задачам на растворы, смеси и сплавы. Однако задачи на смеси часто включают в экзаменационные варианты 11-го, а иногда и 9-го класса, но многие ученики пропускают эти задачи, так как испытывают сложности при их решении.
Задачи на смеси и сплавы имеют практическое значение, являются хорошим средством развития мышления учащихся. Они расширяют базовый курс математики и позволяют учащимся осознать практическую ценность математики. Задачи на растворы, смеси и сплавы обладают диагностической и прогностической ценностью, то есть с их помощью можно проверить знания основных разделов школьной математики, уровень математического и логического мышления, первоначальные навыки исследовательской деятельности, то есть лишний раз проверить и оценить свои способности к математике. При решении задач на растворы, смеси и сплавы очевидны межпредметные связи с химией, физикой и экономикой, знание этого повышает учебную мотивацию учащихся по всем предметам.
Трудности при решении этих задач могут возникнуть на различных этапах:
составления математической модели ( уравнения, системы уравнений, неравенства)
решения полученной модели;
анализа математической модели ( по причине кажущейся ее неполноты: не хватает уравнений в системе или слишком много неизвестных и пр.)
Все сложности преодолимы при тщательном анализе задачи. Этому способствуют рисунки, чертежи, схемы, таблицы и пр. Очень важно разобраться в самом тексте задачи, вникнуть в условия, составить алгоритм решения. Каждый учащийся сам  себя делает вывод об уровне сложности той или иной задачи и месте, где эта сложность возникает.
себя делает вывод об уровне сложности той или иной задачи и месте, где эта сложность возникает.
Теоретические основы решения задач «на смеси, сплавы, растворы».
Перед тем как приступить к объяснению различных способов решения подобных задач, примем некоторые основные допущения.
Говоря о смесях, растворах и сплавах будем употреблять термин «смесь» не зависимо от ее вида (твердая, жидкая, сыпучая, газообразная). Смесь состоит из основного вещества и примеси. Что берется за основное вещество, в каждой задаче определяется отдельно.
При решении этих задач считается, что масса смеси нескольких веществ равна сумме масс компонентов, что отражает закон сохранения массы.
Определение. Процентным содержанием (концентрацией) вещества в смеси называется отношение его массы к общей массе всей смеси.
Эта величина может быть выражена либо в дробях, либо в процентах.
Измерять количество компонентов в смеси будем в единицах массы, а не объема, т.к. изменение массы происходят линейно, а изменение объема – по более сложной зависимости, и все равно приходится переходить к изменениям массы, но уже используя плотность веществ.
Концентрация – это безразмерная величина.
Сумма массовых долей всех компонентов, составляющих смесь, очевидно, равна единице.
Различные способы решения задач
В дальнейшем в начале каждой задачи указано, начиная с какого класса можно ее решать. Это позволит учителю сэкономить время при подготовке к уроку, так как одну и ту же задачу можно использовать в 5-м или 6-м классе при изучении темы, а потом ее включить при повторении в 9-м или 11-м классе. В процессе решения задач учащиеся повторяют как найти часть от числа и число по его части, прямую и обратную пропорциональные зависимости, способы решения уравнений и другое.
1. В колбе было 140 г 10%-го раствора марганцовки (перманганата калия). В нее долили 60 г 30%-го раствора марганцовки. Определите процентное содержание марганцовки в полученном растворе.
Условия задач на смеси удобно записывать в виде таблицы, и надо приучать учащихся к такой записи.
Решение. Заполним таблицу по условию задачи:
|
| а | М (г) | m (г) |
| Было | 10% или 0,1 | 140 | 0,1*140 |
| Добавили | 30 % или 0,3 | 60 | 0,3*60 |
| Стало | ? | 140+60 |
|
1) 0,1 140 + 0,3 60 = 32 г — масса марганцовки в смеси;
2) 140 + 60 = 200 г масса смеси;
3) а=i10О=16% — содержание марганцовки в смеси.
Ответ: 16%
Рассмотрим другую задачу, которая получена из первой небольшим изменением условия.
2. Сколько нужно взяты 10%-го и 30%-го растворов марганцовки, чтобы получить 200 г 16%-го раствора марганцовки?
Решение. Способ I. (С 5-го класса.) Пусть масса первого раствора — х г. Заполним таблицу по условию задачи:
|
| а | М(г) | m(г) |
| 1-й раствор | 10 % или 0,1 | Х | 0,1х |
| 2-й раствор | 30% или 0,3 | 200-х | 0,3(200-х) |
| 3-й раствор | 16 % или 0,16 | 200 | 0,16*200 |
Составим и решим уравнение: 0,Iх + 0,3(200 — х) = 0,16 *200, 0,2х = 28, откуда
х = 140.
Ответ: 140 г 10%-го и 60 г 30%-го.
Способ II. (С 7-го класса.) Пусть масса первого раствора — х г, а масса второго раствора — у г. Заполним таблицу по условию задачи:
|
| а | М(г) | m(г) |
| 1-й раствор | 10 % или 0,1 | Х | 0,1х |
| 2-й раствор | 30% или 0,3 | y | 0,3y |
| 3-й раствор | 16 % или 0,16 | 200 | 0,16*200 |
Составим и решим систему уравнений:
х+у=200, х=200—у, х=140,
0,1х+0,3у=32; 0,1(200—у)+0,зу=32; у=б0.
Ответ: 140 г 10%-го и 60 г 30%-го.
Способ III. Решим эту задачу старинным способом по правилу
«креста».
Составим схему:
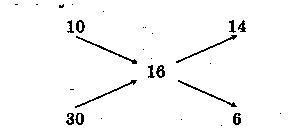
В левой колонке схемы записаны процентные содержания марганцовки в имеющихся растворах. Посередине — процентное содержание марганцовки в полученной смеси. В правой — разности процентных содержаний имеющихся растворов и полученной смеси (вычитаем из большего числа меньшее и записываем разность на ту диагональ, где находятся, соответственно, уменьшаемое и вычитаемое).
Исходя из схемы делаем вывод: в 200 г смеси содержится 14 частей 10%-го раствора и 6 частей 30%-го раствора. Найдем их массы:
200:(14+6)14=140г; 200 : (14 + 6) .6 = 60 г.
Ответ: 140 г 10%-го и 60 г 30%-го.
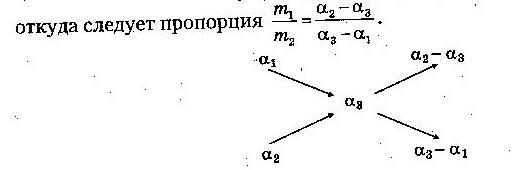
В старших классах можно показать, как выводится правило «креста». Пусть смешали два раствора: первый — массой m1 г и концентрацией a1 и второй — массой m2 г и концентрацией а2, получили раствор массой (m1 + m2) г и концентрацией а, причем а1 3 2.
Найдем зависимость масс исходных растворов от их концентраций.
Масса основного вещества в первом растворе равна a1m1, во втором растворе —, а2 m2г, а в смеси a3 (m1 + m2) г.
Составим равенство a1m1+ а2m2 = a3(m1 + m2) и из него получим:
a1m1 - а3 m1 = a3m2 - а2m2
3. Имеется склянка 20%-го раствора кислоты и склянка 40%-го раствора кислоты.
а) Смешали 200 г раствора кислоты из первой склянки и 300 г из второй. Определите массу кислоты и ее долю в полученном растворе.
б) Из первой склянки взяли 300 г раствора кислоты. Сколько
граммов раствора кислоты надо долить из второй склянки, чтобы
получить 32%-й раствор кислоты?
в) Верно ли, что если из второй склянки берут на 50% больше
раствора кислоты, чем из первой, то полученная смесь является
32%-ым раствором кислоты?
Решение, а) Заполним таблицу по условию задачи:
|
| а | М(г) | m(г) |
| 1-й раствор | 20 % или 0,2 | 200 | 0,2*200 |
| 2-й раствор | 40% или 0,4 | 300 | 0,4*300 |
| смесь | ? | 200+300 | ? |
Масса кислоты в смеси: 0,2. 200 + 0,4 . 300 = 40 + 120 160 г.
Процентное содержание кислоты в смеси рассчитаем по формуле:
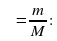
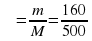 ∙ 100=32%
∙ 100=32%
Ответ: 160 г, 32%.
б) Пусть из второй склянки взяли х г раствора кислоты. Заполним таблицу по условию задачи.
|
| а | m(г) | М(г) |
| 1-й раствор | 20 % или 0,2 | 0,2*300 | 300 |
| 2-й раствор | 40% или 0,4 | 0,4х | Х |
| смесь | 32% или 0,32 | 60+0,4х | 300+х |
Составим и решим уравнение: 60 + 0,4х = 0,32 (300 + х),0,08х = 36,
откуда х = 450. Ответ: 450 г.
в) Пусть из первой склянки берут х г раствора. Заполним таблицу по условию задачи.
|
| а | М(г) | m(г) |
| 1-й раствор | 20 % или 0,2 | Х | 0,2х |
| 2-й раствор | 40% или 0,4 | 1,5х | 0,4 *1,5х |
| смесь | 32% или 0,32 | Х+1,5х | 0,32 *2,5х |
Рассчитаем содержание кислоты в смеси по формуле 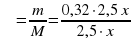 ∙ 100=32%
∙ 100=32%
Ответ: верно.
Задачи на понижение концентрации
1.(С 5-го класса) Сироп содержит 18% сахара. Сколько килограммов воды нужно добавить к 40 кг сиропа, чтобы содержание сахара составило 15%?
Решение. Пусть надо добавить х кг воды. Заполним таблицу по условию задачи.
|
| а | М(г) | m(г) |
| Было | 18% или 0,18 | 40 | 0,18*40 |
| стало | 15% или 0,15 | 40+х | 0,15*(40+х) |
Так как масса сахара не изменилась, то составим и решим уравнение:
0,15(40 + х) = 7,2, О,15х = 1,2, откуда х = 8.
Ответ: 8 кг
2. (С 6-го класса) Сколько килограммов 5%-го раствора соли надо добавить к 15 кг 10%-го раствора той же соли, чтобы получить ее 8%-ный раствор?
Решение. Пусть добавили х кг 5%-го раствора соли. Заполним таблицу по условию задачи:
| Раствор | а | М(кг) | m(кг) |
| 10%-ный | 10%или 0,1 | 15 | 0,1*15 |
| 5%-ный | 5% или 0,05 | Х | 0,05х |
| 8%-ный | 8% или 0,08 | 15+х | 1,5+0,05х |
Составим и решим уравнение: 1,5 + 0,05х = 0,08 (15 + х), 0,ОЗх= 0,3,
откуда х= 10.
Ответ: 10 кг.
Задачи на «высушивание»
При решении этих задач надо объяснить учащимся , что все тела, вещества, продукты содержат в себе воду, которая частично испаряется. Поэтому при решении этих задач мы каждый раз разделяем данное нам вещество на воду и «сухой остаток», масса которого не меняется в условиях задачи.
1. (С5-го класса) Трава при высыхании теряет около 28% своей массы. Сколько было накошено травы, если из нее было получено 1,44 т сена?
Решение. Заполним таблицу по условию задачи:
|
| Масса в тоннах | Содержание в % |
| Трава | Х | 100 |
| сено | 1,44 | 100-28 |
Зависимость прямо пропорциональная. Составим и решим пропорцию 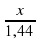 =
= 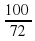 , откуда х =
, откуда х =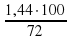 =2 т Ответ: 2 т.
=2 т Ответ: 2 т.
2. (С 6-го класса) Имеется 0,5 т целлюлозной массы, содержащей 85% воды. После выпаривания получили массу, содержащую 25% целлюлозы. Сколько килограммов воды было выпарено?
Решение. Пусть выпарили х кг воды. Заполним таблицу по условию задачи:
|
| α% | М кг | m кг |
| Было | 100-85 | 500 | 500 ∙0,15 |
| стало | 25 | 500-х | (500-х) ∙ 0,25 |
Составим и решим уравнение: 5000,15 = (500 — х)0,25, 0,25х = 50, откуда х = 200.
Ответ: 200 кг.
3. (С 6-го класса) Из 60%-го водного раствора спирта испарилась половина воды и 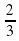 спирта. Каково процентное содержание спирта в получившемся растворе?
спирта. Каково процентное содержание спирта в получившемся растворе?
Решение. 60%-й раствор спирта содержит 60% спирта и 100—60=40% воды. Если масса раствора была х г, то спирта в нем было 0,6х г, а воды — 0,4х г. В результате испарения в растворе осталось:
1) спирта 1-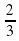 =
= 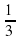 , или
, или 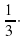 О,6х=О,2х г;
О,6х=О,2х г;
2) воды 1- 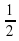 =
= 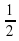 , или
, или  ∙ 0,4х=0,2х г.
∙ 0,4х=0,2х г.
Рассчитаем концентрацию получившегося раствора:
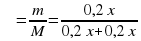 =
= 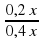 =
= 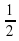 = 50%
= 50%
Ответ: 50%.
Задачи на смешивание растворов разных концентраций
1. .(С 6-го класса) При смешивании 5%-го и 40%-го растворов кислоты получили 140 г 30%-го раствора кислоты. Сколько грамм каждого раствора было взято?
Решение. Пусть взяли х г 5%-го раствора кислоты. Заполним таблицу по условию задачи:
|
| α г | М г | m г |
| 5%-ный | 0,05 | Х | 0,05х |
| 40%-ный | 0,4 | 140-х | 0,4 (140-х) |
| смесь | 0,3 | 140 | 0,3 ∙ 140 |
Составим и решим уравнение:
0,05х + 0,4(140 — х) = 0,3 ∙ 140, 0,35х = 14, х = 40.
Ответ: 40 г 5%-го и 100 г 40%-го.
2. Один сплав, состоящий из двух металлов, содержит их в отношении 1 : 2, а другой — в отношении 2 : З. Сколько частей каждого сплава нужно взять, чтобы получить сплав, содержащий эти металлы в отношении 17: 27?
Решение. Пусть нужно взять х частей первого сплава и у частей второго.
В х частях первого сплава будет 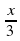 частей одного металла и
частей одного металла и 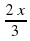 другого. В y частях второго сплава будет
другого. В y частях второго сплава будет 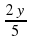 и
и 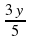 частей одного и другого металла.
частей одного и другого металла.
Составим уравнение по условию задачи: (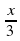 +
+ 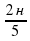 ): (
): (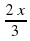 +
+ 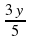 )=
)=
Умножив числитель и знаменатель левой дроби на 15, получим уравнение
=  откуда получим: 135х + I62у = 170х + I53у, 35х = 9у,
откуда получим: 135х + I62у = 170х + I53у, 35х = 9у,  =
= 
Ответ: 9 частей первого и 35 частей второго.
Задачи на повышение концентрации
1. (С 6-го класса.) Сплав массой 36 кг содержит 45% меди. Сколько меди нужно добавить, чтобы новый сплав содержал 60% меди?
Решение. 45% — это 0,45, 360,45 = 16,2 кг меди содержится в данном сплаве.
Пусть масса меди, которую надо добавить в сплав, равна х кг, тогда (36 + х) кг — масса сплава после добавления меди, а масса меди в новом сплаве (16,2 + х) кг. Зная, что медь в новом сплаве составила 60%, составим и решим уравнение: 16,2 + х = (36 + х) Х Х 0,6, 0,4х= 5,4, откуда х = 13,5.
Ответ: 13,5 кг.
2. (С 8-го класса.) В сплаве олова и меди содержалось 11 кг меди. После того как в сплав добавили 7,5 кг олова, концентрация олова повысилось на 33%. Какова первоначальная масса сплава?
Решение. Пусть первоначальная масса сплава х кг, в нем содержалось 11 кг меди и (х —11) кг олова. Заполним таблицу по условию задачи:
|
| M кг | M (олова) кг | α % |
| Было | Х | Х-11 |  ∙ 100 ∙ 100
|
| стало | Х+7,5 | Х-11+7,5=х-3,5 |  ∙ 100 ∙ 100
|
Составим и решим уравнение:
 ∙ 100 –
∙ 100 –  ∙ 100 = 33
∙ 100 = 33
IООх (х — 3,5) — 100(х + 7,5)(х — 11) = ЗЗх (х + 7,5),
22х2+165х—5500=0. D =27225+484000=511 225.
Х1,2 = ; х1 =
; х1 =  = 12,5;
= 12,5;
Х2 0). Значит, первоначальная масса сплава 12,5 кг.
Ответ: 12,5 кг.
Задачи вариантов единого государственного экзамена
Впервые в вариантах единого государственного экзамена по математике задача на «смеси и сплавы» появились в 2003 году в заданиях группы В, в 2004 и в 2005 годах такие задачи также были представлены в вариантах единого экзамена.
|
|
| 2003 ЕГЭ | К 120 г раствора, содержащего 80% соли, добавили 480 г раствора, содержащего 20 % той же соли. Сколько процентов соли содержится в получившемся растворе? |
| | Решение. 1) 0,8*120=96(г)-соли в первоначальном растворе; 2) 480*0,2=96(г) соли во втором растворе; 3) ((96+96)/(120+480))*100%=32%-процентное содержание соли в получившемся растворе. Ответ: 32% |
|
|
|
|
|
|
| 2004 ЕГЭ | Имеются два слитка сплава золота с медью. Первый слиток содержит 230 г золота и 20 г меди, а второй слиток – 240 г золота и 60 г меди. От каждого слитка взяли по куску, сплавили их и получили 300 г сплава, в котором оказалось 84 % золота. Определить массу ( в граммах) куска, взятого от первого слитка. |
| | Решение. Определим процентное содержание золота в обоих слитках. 1) 230+20=250(г)-масса 1 слитка, 230/250=0,92 (92%)процентное содержание золота в 1 слитке. 2) 240+60=300(г) –масса 2 слитка, 240/300=0,8 (80%)- процентное содержание золота во 2 слитке. Пусть х масса куска, взятого от 1 слитка, (300-х)- масса куска, взятого от 2 слитка, получим уравнение 0,92х+0,8(300-х)=0,84*300, откуда х=100 Ответ: 100г. |
| 2004 ЕГЭ | Первый сплав серебра и меди содержит 70 г меди, а второй сплав – 210 г серебра и 90 г меди. Взяли 225 г первого сплава и кусок второго сплава, сплавили их и получили 300 г сплава, который содержит 82 % серебра. Сколько граммов серебра содержалось в первом сплаве? |
| | Решение. Пусть х г серебра содержится в 1 сплаве., тогда 70/(х+70)-какую часть 1 сплава составляет медь, 90/(210+90)-такую часть составляет медь во 2 сплаве., кусок второго сплава 300-225=75г, тогда получаем уравнение. 225*(70/(х+70))+75*(90/300)=(1-0,82)*300, откуда х=430г Ответ: 430г |
| ЕГЭ 2004 | В колбе было 200 г 80% -го спирта. Провизор отлил из колбы некоторое количество этого спирта и затем добавил в нее столько же воды, чтобы получить 60% - ый спирт. Сколько граммов воды добавил провизор?. |
| | Решение. 200*0,8=160(г)-масса чистого спирта в колбе, их колбы отлили х г раствора, осталось (200-х)г раствора, в котором чистого спирта 0,8*(200-х). Когда к раствору добавили х г воды, то масса раствора снова стала 200 г, а концентрация [(0,8*(200-х))/200]*100%=60%, откуда х=50(г). Ответ: провизор добавил 50г воды. |
| ЕГЭ 2004 | В колбе было 800 г 80% -ного спирта. Провизор отлил из колбы 200 г этого спирта и добавил в нее 200 г воды. Определить концентрацию ( в процентах) полученного спирта. |
| | Решение. После того, как провизор отлил 200 г раствора, стало 600г, в котором чистого спирта 0,8*600=480г, когда добавили200г воды, то раствор снова 800г, а концентрация чистого спирта в растворе (480/800)*100%=60% Ответ: 60% |
| ЕГЭ 2005 | Из сосуда, доверху наполненного 94% -м раствором кислоты, отлили 1,5 л жидкости и долили 1,5 л 70% -го раствора этой же кислоты. После этого в сосуде получился 86% раствор кислоты. Сколько л раствора вмещает сосуд? |
| | Решение. Пусть х л вмещает сосуд, тогда из условий задачи следует уравнение 0,94(х-1,5)+0,7*1,5=0,86х, откуда х=4,5 л. Ответ: 4,5 л |
Задачи, взятые из различных пробных, репетиционных, диагностических и тренировочных работ 2010-2011 гг.
Смешали некоторое количество 15 процентного раствора некоторого вещества с таким же количеством 19 процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
Смешали 30%-вьй раствор соляной кислоты с 10%-ным и получили 6ООг 15%-го раствора Сколько граммов 1 0%-го раствора было взято?
Имеется два сплава. Первый содержит 5% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 225 кг, содержащий 20% никеля. На сколько килограммов масса первого сплава меньше массы второго?
Имеется два сплава с разным содержанием золота. В первом сплаве содержится 35% золота, а во втором — 60%. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 40% золота?
При смешивании первого раствора кислоты, концентрация которого 20%. и второго раствора этой ж кислоты концентрация которого 50%, получили раствор, содержащий 30% кислоты. В каком отношении были взяты первый второй растворы?
Смешали З литра 40-процентного водного раствора некоторого вещества с 12 литрами 35-процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Смешали 8 литров 15-процентного водного раствора некоторого вещества с 12 литрами 40-процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Смешали некоторое количество 17-процентного раствора некоторого вещества со втрое большим количеством 9-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
Смешали некоторое количество 14-процентного раствора некоторого вещества со вдвое большим количеством 8-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
Заключение
Задачи выбраны по справочникам и учебным пособиям, по экзаменационным материалам, в том числе и вариантам ЕГЭ, на изменение концентрации веществ в смесях и распределены по блокам. Собранный материал можно использовать на уроках и для самоподготовки учащихся. Для большей наглядности обучения используется разное оформление решений и заполнения таблиц.
Литература
Копылова Н.П. Решебник «Задачи на смеси и сплавы» 2005г. г.Шелехов.
Прокопенко Н.И. «Задачи на смеси и сплавы» 2010г. г. Москва
ЕГЭ Математика 2011 г. ФИПИ-М…Интеллект-Центр,2011.-144с.
Под редакцией Ф.Ф.Лысенко «Тематические тесты» Издательство «Легион-М»,2010
Мальцев Д.А., Мальцева Л.И. «Математика. Все для ЕГЭ 2011» 2010г. г.Москва
http://www.fipi.ru

 Получите свидетельство
Получите свидетельство Вход
Вход



 себя делает вывод об уровне сложности той или иной задачи и месте, где эта сложность возникает.
себя делает вывод об уровне сложности той или иной задачи и месте, где эта сложность возникает.

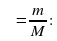
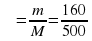 ∙ 100=32%
∙ 100=32%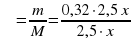 ∙ 100=32%
∙ 100=32%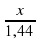 =
= 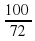 , откуда х =
, откуда х =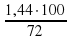 =2 т Ответ: 2 т.
=2 т Ответ: 2 т.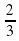 спирта. Каково процентное содержание спирта в получившемся растворе?
спирта. Каково процентное содержание спирта в получившемся растворе?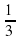 , или
, или 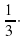 О,6х=О,2х г;
О,6х=О,2х г;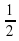 =
=  ∙ 0,4х=0,2х г.
∙ 0,4х=0,2х г.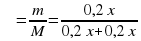 =
= 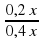 =
= 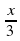 частей одного металла и
частей одного металла и 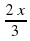 другого. В y частях второго сплава будет
другого. В y частях второго сплава будет 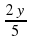 и
и 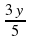 частей одного и другого металла.
частей одного и другого металла.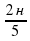 ): (
): (








 Проектная работа по математике на тему: «Методика подготовки учащихся к решению задач по теме: задачи на смеси и сплавы, включенных в ЕГЭ по математике» (68.14 КB)
Проектная работа по математике на тему: «Методика подготовки учащихся к решению задач по теме: задачи на смеси и сплавы, включенных в ЕГЭ по математике» (68.14 КB)
 0
0 2116
2116 193
193 Нравится
0
Нравится
0


