
МБОУ СОШ № 31 10 класс, геометрия
Урок пол теме «Задачи на построение сечений параллелепипеда»
Учитель: Кряквина Л.Н.

Содержание
- 1. Основные принципы построения сечений параллелепипеда.
- 2. Примеры.
- 3. Вопросы для самопроверки.
- 4. Задачи.

Основные принципы построения сечений (1)
- Секущая плоскость пересекает грани параллелепипеда по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением параллелепипеда. Параллелепипед имеет шесть граней. Его сечениями могут быть треугольники, четырехугольники, пятиугольники, шестиугольники.

Основные принципы построения сечений (2)
- Если секущая плоскость пересекает две противоположные грани по каким-то отрезкам, то эти отрезки параллельны.
- Для построения сечения достаточно построить точки пересечения секущей плоскости с ребрами параллелепипеда, после чего остается провести отрезки соединяющие каждые две точки, лежащие в плоскости одной грани.

Примеры построения сечений
- Объясните, как построить сечение куба плоскостью, проходящей через три данные точки, являющиеся либо вершинами куба, либо серединами его ребер (три данные точки на рисунках выделены).
- В задачах 1 – 4, 6 найдите периметр сечения, если ребро куба равно a .
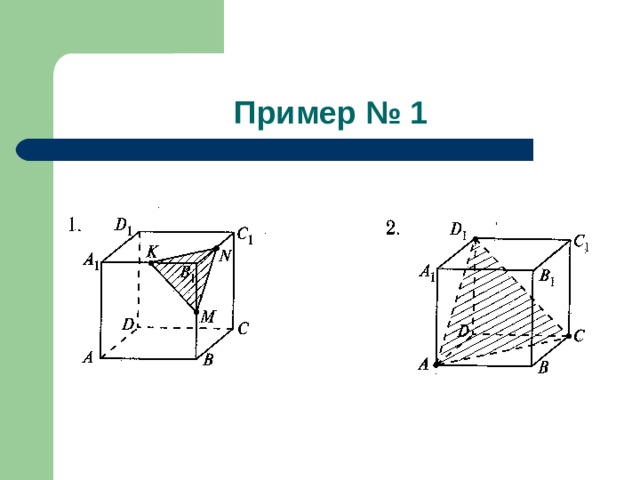
Пример № 1
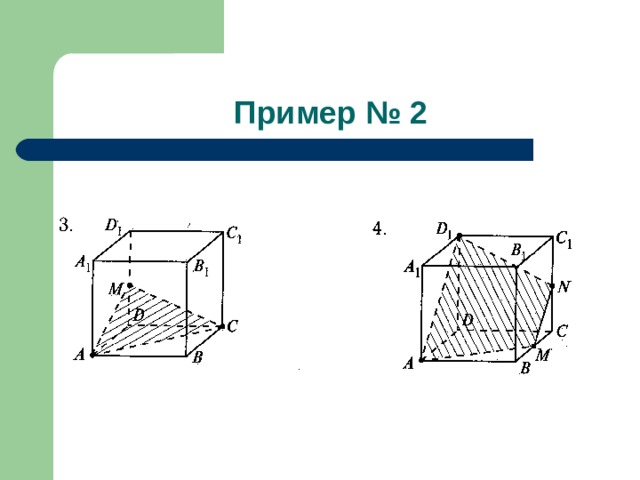
Пример № 2
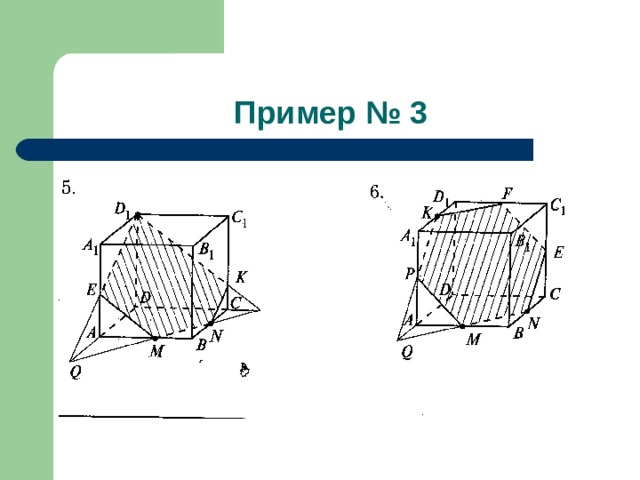
Пример № 3

Проверь свое решение
- Ответы:
- К рисунку № 1: (3 a)/ √ 2
- К рисунку № 2: 3a √ 2
- К рисунку № 3: a √ 2+a √ 5
- К рисунку № 4: 1 ,5 a √ 2+a √ 5
- К рисунку № 6: 3a √ 2

Вопросы для самопроверки
- 1. Сколько вершин, ребер, граней имеет параллелепипед?
- 2. Какие вершины в параллелепипеде называются противоположными?
- 3. Какие многоугольники могут быть в сечении параллелепипеда?
- 4. Почему секущая плоскость пересекает противоположные грани параллелепипеда по параллельным отрезкам?

Задачи

Задача № 1
- Три ребра параллелепипеда равны 3 см, 4 см и 5 см. Найдите сумму длин всех его ребер.
- 1. 48 см
- 2. 36 см
- 3. 12 см
- 4. 28 см

Задача № 2
- ABCDA 1 B 1 C 1 D 1 – прямоугольный параллелепипед, AB=AD= 8 дм, АА 1 = 2 дм. Найдите площадь сечения BMKD , где М –середина В 1 С 1 и К – середина С 1 D 1 .
- 1. 3 √ 15 см 2
- 2. 12 √ 6 см 2
- 3. 6 √ 6 см 2
- 4. 15 √ 3 см 2

Задача № 3
- ABCDA 1 B 1 C 1 D 1 – куб. К – середина ребра AD , М –середина CD . В каком отношении, считая от точки А, делит ребро АА 1 плоскость, проходящая через точки В 1 , К и М?
- 1. 1:1
- 2. 1:2
- 3. 1:3
- 4. 1:4

К сожалению, Вы ошиблись.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Задачи на построение сечений (244.5 KB)
Задачи на построение сечений (244.5 KB)
 0
0 557
557 8
8 Нравится
0
Нравится
0






