Готовимся к экзаменам. Решение задач на концентрацию, смеси, сплавы.
Задачам на концентрацию, смеси, сплавы в школьном курсе математики мало уделяется внимания. Но они часто встречаются в тестах на выпускных экзаменах и вызывают затруднения у учащихся.
При решении задач принимают такие допущения:
процент величины - одна сотая часть этой величины;
если число a составляет p % от числа b, то эти числа связаны равенством
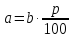 ;
;все полученные сплавы, растворы, смеси считаются однородными;
при соединении растворов и сплавов не учитываются химические взаимодействия их отдельных компонентов;
если два сплава (раствора) соединяют в один сплав (раствор), то выполняются равенства: V=V1+V2 - сохраняется объем и m=m1+m2 - сохраняется масса.
Объемная (массовая) концентрация есть число, показывающее, какую долю всего объема (массы) составляет данный компонент.
Если сплав (раствор, смесь) имеет массу m и состоит из веществ A, B, C, массы которых соответственно
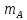 ,
, 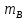 ,
, 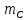 , то величины
, то величины 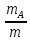 ,
, 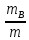 ,
, 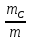 называют концентрацией веществ A, B, C, а величины
называют концентрацией веществ A, B, C, а величины 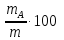 ,
,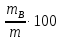 ,
, 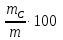 - процентным содержанием веществ. При этом справедливо равенство
- процентным содержанием веществ. При этом справедливо равенство 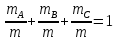 .
. Например, если имеется 40%-ный раствор соли, то в этом растворе 0,4 объема занимает соль. Значит, объемная концентрация соли в растворе равна 0,4. Если сплав содержит свинец и медь в отношении 4 : 7, то
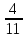 массы всего этого сплава составляет свинец, а
массы всего этого сплава составляет свинец, а 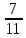 - медь, т. е., массовые концентрации свинца и меди в сплаве соответственно равны
- медь, т. е., массовые концентрации свинца и меди в сплаве соответственно равны 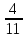 и
и 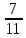 .
.
Алгоритм решения задачи на сплавы, растворы и смеси:
Изучить условия задачи. Выбрать неизвестные величины (их обозначают буквами х, у и т.д.), относительно которых составить пропорции, этим, мы создаем математическую модель ситуации, описанной в условии задачи.
Используя условия задачи, определить все взаимосвязи между данными величинами.
Составить математическую модель задачи и решить ее.
Изучить полученное решение, провести критический анализ результата.
В большинстве случаев задачи на смеси и сплавы становятся нагляднее, если при их решении использовать схемы в виде:
| Объем данного раствора
| Объем данного раствора | Объем данного раствора | |||||
| Раствор 1 +
| Раствор 2 =
|
| |||||
| Вещество 1
| Вещество 2 | Вещество 1 | Вещество 2 | Вещество 1 | Вещество 2 | ||
| Данные о веществах | Данные о веществах | Данные о веществах | |||||
Пример 1. В бидон налили 4 литра молока 3% жирности и 6 литров 6% жирности. Сколько % составляет жирность молока в бидоне?
| 4л | 6л | 4л+6л=10л | |||||
| Раствор 1 + | Раствор2 = | Раствор3 | |||||
|
|
|
| |||||
| молоко | жир | молоко | жир | молоко | жир | ||
|
| 3% |
| 6% |
| Х%
| ||
Составляем уравнение:
0,12 +0,36=0,1х
Х=4,8.
Ответ: жирность молока в бидоне 4,8%.
Пример 2. В первом сосуде 500мл 70% раствора кислоты, во втором 200мл 90% раствора этой же кислоты. Сколько мл раствора нужно перелить из второго сосуда в первый, чтобы в первом получился 75% раствор кислоты?
| 500 мл | Х мл | (500+х) мл | |||||
| Раствор 1 + | Раствор 2 = | Раствор3 | |||||
|
|
|
| |||||
| кислота | вода | кислота | вода | кислота | вода | ||
| 70% |
| 90% |
| 75%
|
| ||
Составляем уравнение:
+
=
,
350+0,9х=375+0,75х,
0,15х=25,
Х=.
Ответ: мл раствора нужно перелить из второго сосуда в первый.
Пример 3. Один раствор содержит 20% соляной кислоты, а второй 70% кислоты по объему. Сколько литров первого и второго растворов нужно взять, чтобы получить 100 литров 50% раствора?
| хл | (100-х)л | 100л | |||
| Раствор 1 + | Раствор2 = | Раствор3 | |||
|
|
|
| |||
| кислота | вода | кислота | вода | кислота | вода |
| 20% |
| 70% |
| 50%
|
|
Составляем уравнение:
+
=
,
0,2х+0,7(100-х)=50,
Х=40.
100-40=60.
Ответ: 40л первого раствора и 60л второго нужно взять.
Пример 4. Из сосуда, содержащего 10 % спирт, отлили одну треть, долили воды допервоначального объема. Сколько процентов спирта в данном сосуде?
| Х л | Х- | | ||||||||||||
| Раствор 1 – Раствор 1 | | | ||||||||||||
|
|
|
| ||||||||||||
| кислота | вода | кислота | вода | кислота | вода | спирт | вода | |||||||
| 10% |
| 10% |
| 10% |
| ? % |
| |||||||
Составляем отношение:
Ответ: 8% спирта.
Пример 5. Свежие грибы содержат 90% воды (по массе), а сухие -12% воды. Сколько получится сухих грибов из22 кг свежих и сколько надо собрать свежих, чтобы получить 200г сухих?
| 22 кг |
| Х кг | |||||
| Свежие грибы - | вода = | Сухие грибы | |||||
|
|
|
| |||||
| вещество | вода |
|
| вещество | вода | ||
| 1000%-90%=10% | 90%
|
|
| 100%-12%=88%
| 12%
| ||
Составляем уравнение:
,
0,88х=2,2,
Х=2,5.
| х г |
| 200 кг | |||||
| Свежие грибы - | вода = | Сухие грибы | |||||
|
|
|
| |||||
| вещество | вода |
|
| вещество | вода | ||
| 1000%-90%=10% | 90%
|
|
| 100%-12%=88%
| 12%
| ||
Составляем уравнение:
,
0,1х=176,
Х=1760.
Ответ: получится 2,5кг сухих грибов и потребуется 1760г сырых.
Пример 6. Влажность сухой цементной смеси на складе составляет 18%. Во время перевозки из-за дождей влажность повысилась на 2%. Найдите массу привезенной смеси, если со склада было отправлено 400 кг.
| 400 кг |
| Х кг | |||||
| Смесь 1 + | вода = | Смесь 2 | |||||
|
|
|
| |||||
| вещество | вода |
|
| вещество | вода | ||
| 1000%-18%=82% | 18%
|
|
| 100%-20%=80%
| 18%+2%=20%
| ||
Составляем уравнение:
,
328=0,8х,
Х=410.
Ответ: 410кг.
Пример 7. Первый сплав серебра и меди содержит 430г серебра и 70г меди, а второй сплав – 210г серебра и какое – то количество меди. Сплавили кусок первого сплава с куском массой 75г второго сплава и получили 300г сплава, который содержит 82% серебра. Определите массу (в граммах) второго сплава.
| 430+70=500(г) | 210+х (г) |
| |||
| Сплав 1 | Сплав 2 |
| |||
|
|
|
| |||
| серебро | медь | серебро | медь |
|
|
| 430г | 70г
| 210г | Х г
|
|
|
| 300-75=225(г) | 75г | 300г | ||||
| Сплав 1 + | Сплав 2 = | Сплав 3 | ||||
|
|
|
| ||||
| серебро | медь | серебро | медь | серебро | медь | |
| |
| |
| 82%
|
| |
Составляем уравнение:
=,
193,5+=246,
,
52,5х=4725,
Х=90, 210+90=300(г).
Ответ: 300г масса второго сплава.

 Получите свидетельство
Получите свидетельство Вход
Вход


 Раствор 3
Раствор 3









 "Задачи на концентрацию, смеси и сплавы" (30.28 KB)
"Задачи на концентрацию, смеси и сплавы" (30.28 KB)
 0
0 1905
1905 37
37 Нравится
0
Нравится
0




