Государственное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа № 246
Приморского района Санкт - Петербурга
Методическая разработка урока
по алгебре и началам анализа
для 10 класса
по теме:
«Взаимно-обратные функции»
|
Учитель: Зорина Елена Борисовна |
Цели урока:
Образовательные:
Систематизировать и обобщить знания обучающихся по теме «Степенная функция, её свойства и график», изученной на предыдущих уроках, повторить знания, полученные при изучении в 9 классе темы «Функция».
Познакомить обучающихся с понятием взаимно - обратных функций, условиями существования обратной функции, ее свойствами, сформировать умения необходимые для построения графика обратной функции.
Создать условия для самоконтроля и взаимоконтроля знаний обучающихся.
Развивающие:
Развивать творческую самостоятельность мышления обучающихся, их интеллектуальные качества: способность к «видению» проблемы.
Развивать научную аргументированную речь, умение чётко и ясно излагать свои мысли, исследовать, анализировать, сравнивать, делать выводы, доказательно воспроизводить в процессе деятельности.
Развивать коммуникативные навыки общения и умения слушать и слышать.
Создать условия для освоения приемов использования новых информационных технологий на уроке.
Воспитательные:
Создать условия для становления субъектной позиции обучающихся в различных формах учебного сотрудничества.
Воспитывать умение работать с имеющейся информацией в необычной ситуации.
Воспитывать самостоятельность, аккуратность и добросовестность при выполнении заданий.
Воспитание внимания, самоконтроля, интереса к предмету.
Оборудование:
Магнитно-маркерная белая доска
Компьютер
Мультимедийный проектор Hitachi CP-X3010E
Интерактивная приставка к маркерной доске Mimio Xi Professional
Слайдовая анимированная презентация на электронном носителе.
Тип урока: комбинированный
Формы организации учебной деятельности: полилог, работа с текстом слайда,
индивидуальная исследовательская работа в тетрадях.
Методы: наглядный, словесный, графический, исследовательский.
Этапы урока:
Постановка цели урока и мотивация учебной деятельности. 2 мин
Повторение пройденного материала по теме «Функции и их графики». 11 мин
Этап объяснения нового материала. 10 мин
Физкультминутка. 2 мин
Этап закрепления. 12 мин
Контроль знаний 5 мин
Задание на дом. 1 мин
Рефлексивно-оценочный этап. 2 мин
Ход урока
1. Постановка цели урока и мотивация учебной деятельности
Всем добрый день. Рада вновь видеть вас на своем уроке. Сегодня нам с вами предстоит систематизировать и обобщить знания, полученные на предыдущих уроках теме «Степенная функция, её свойства и график», а также вспомнить всё то, что узнали в 9 классе при изучении темы «Функция».
Ну а затем познакомиться с понятием взаимно-обратных функций, изучить условия существования обратной функции, ее свойства, научиться строить графики обратных функций. Пожелаем друг другу успехов и плодотворной работы.
2. Повторение пройденного материала по теме «Функции и их графики»
| Учитель | Доска | Ученик | ||||||||||||
| Проводит фронтальную работу с классом по слайдам с целью повторить навыки установления соответствия между графическим и аналитическим способами задания функций, изученных ранее. Умения научно и аргументированно обосновать сделанный выбор.
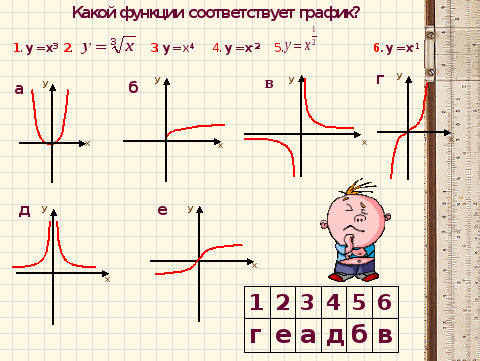
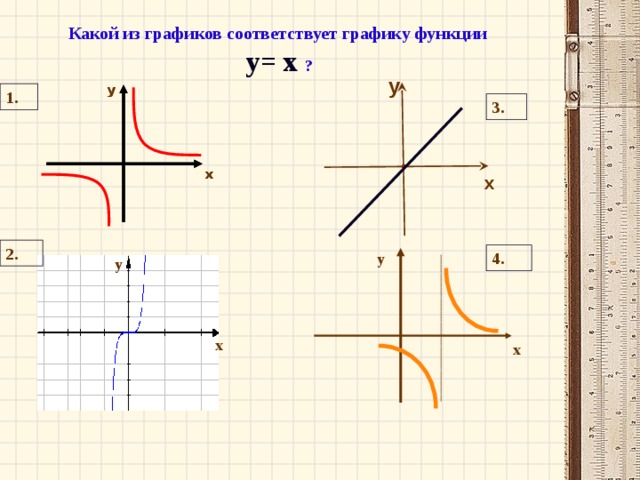
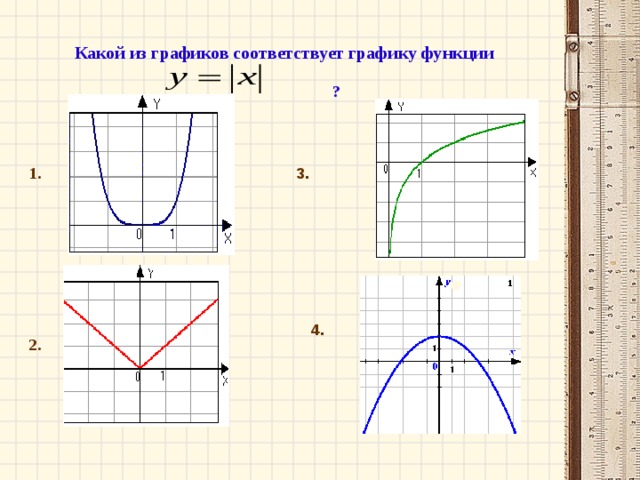
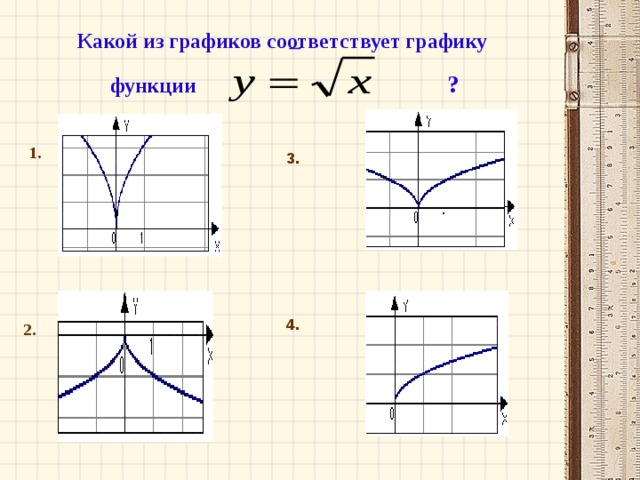
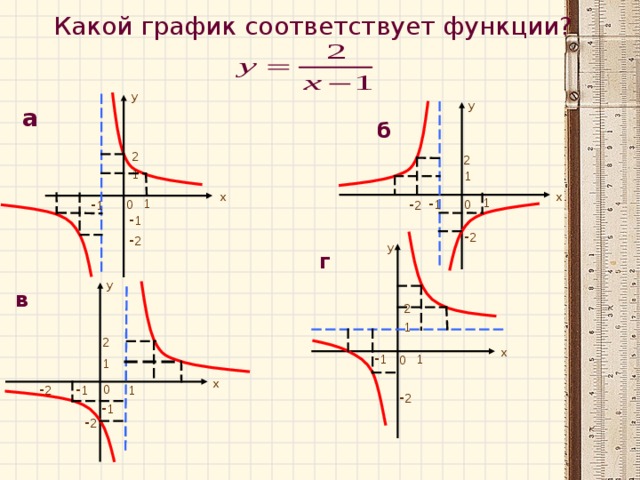
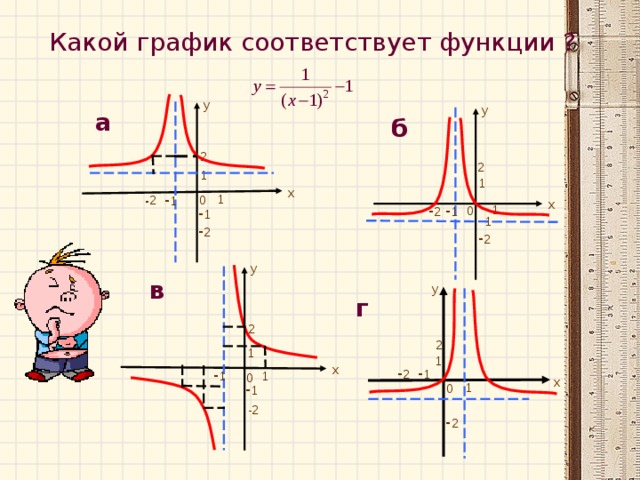
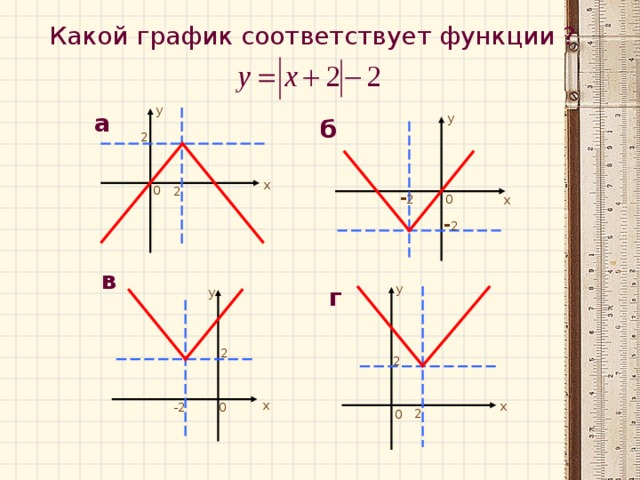
Работа в парах. Установите соответствие между формулой и графиком. Сделайте соответствующую табличку соответствия в тетради. На выполнение работы 2 мин.
После заполнения таблицы учащимися на слайде открыть ответы для последующей проверки.
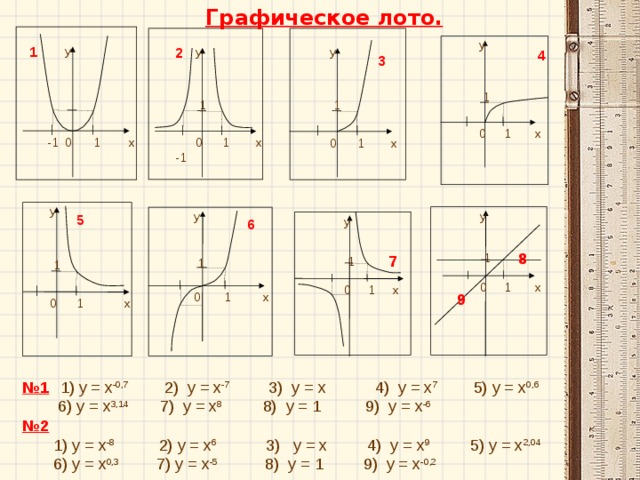
Мы с вами повторили изученный на предыдущих уроках материал, а теперь, пожалуйста, возьмите тестовые листы, лежащие перед каждым из вас. Играем в известное уже вам «Графическое лото». Напоминаю, в результате выполнения задания на соотнесения каждого изображения графика с номером записанной функции, у каждого варианта должно получиться 9-значное число. Работаем быстро, внимательно и самостоятельно. Время – 3 минуты | Слайды 3-11 презентации к уроку.
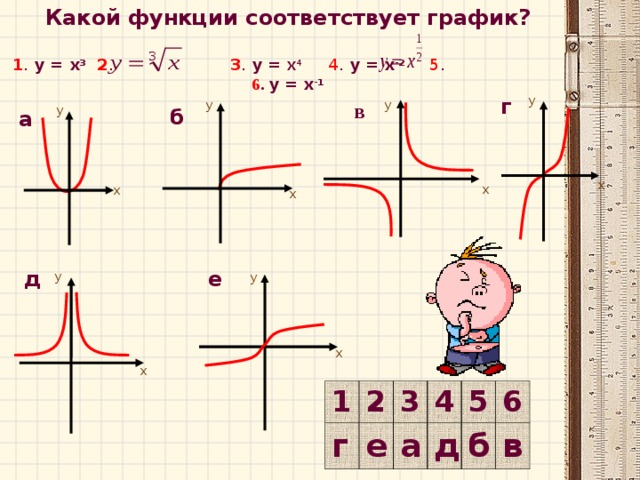
Слайд №12: | Называет номер графика, соответствующего ответу на поставленный вопрос, поясняя и обосновывая свой выбор.
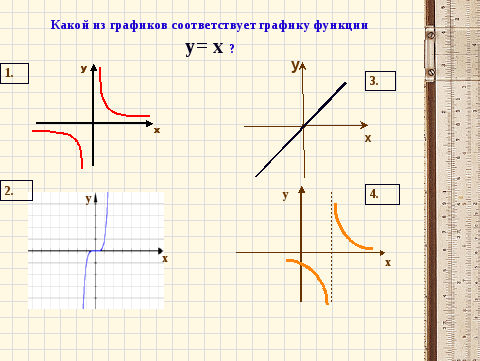
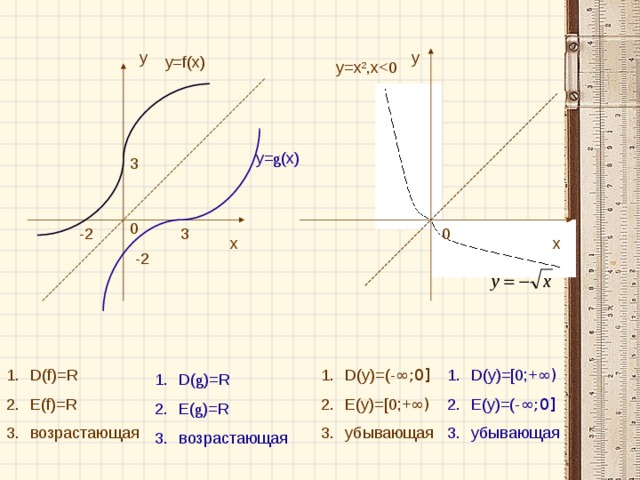
Это формула линейной функции. Графиком её является прямая, значит изображение графика данной функции – это рис. №3.
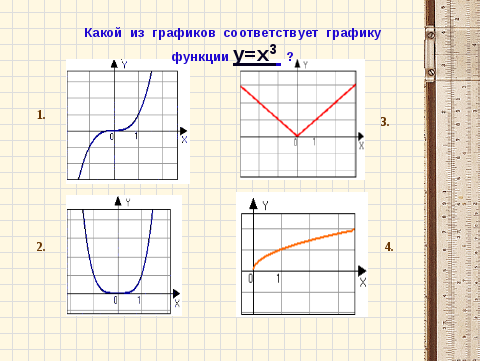
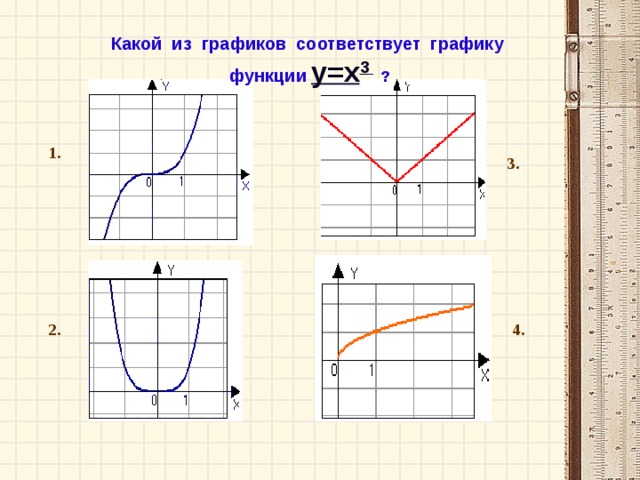
Это формула степенной функции с нечётным натуральным показателем степени. Графиком её является кубическая парабола, значит изображение графика данной функции – это рис. №2.
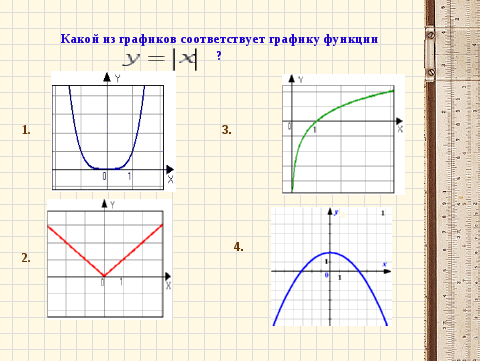
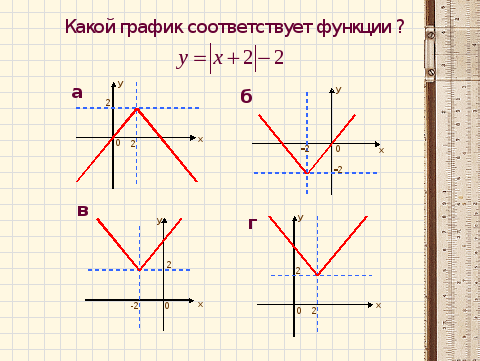
Графиком данной функции является ломаная линия, состоящая из луча с началом в точке (0;0)на неотрицательной части си OX и симметричного для него относительно оси OY луча, значит изображение графика данной функции – это рис. №2.
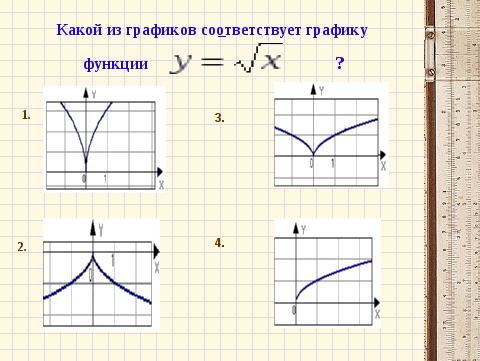
График данной функции – это график степенной функции с показателем степени, представленным положительным действительным числом. Значения x для данной функции могут быть только неотрицательны, т.о. это график рис.4.
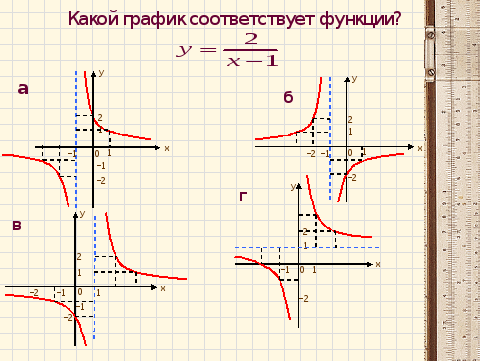
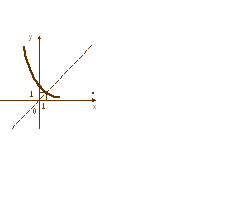
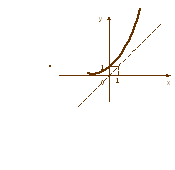
Эта формула – формула прямо пропорциональной зависимости с коэффициентом k=2. График будет расположен в I и III координатных углах и смещён на 1 единицу вправо вдоль оси OX. Это рис.в.
Степенная функция с показателем степени «-2». Ветви её графика располагаются в I и II координатных углах и смещены на 1 единицу вправо вдоль оси OX и на 1 единицу вниз по оси OY (рис.г)
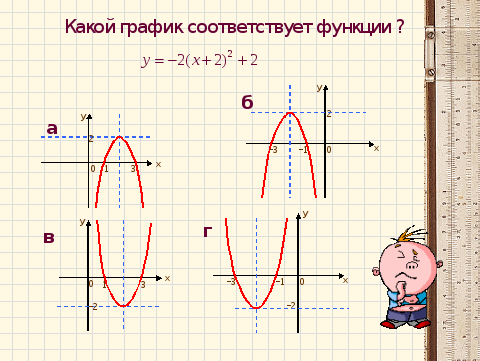
Записана формула квадратичной функции. Графиком записанной функции будет парабола ветви, которой направлены вниз и смещённая вдоль оси OX на 2 единицы влево и вдоль оси OY на 2 единицы вверх (рис. б)
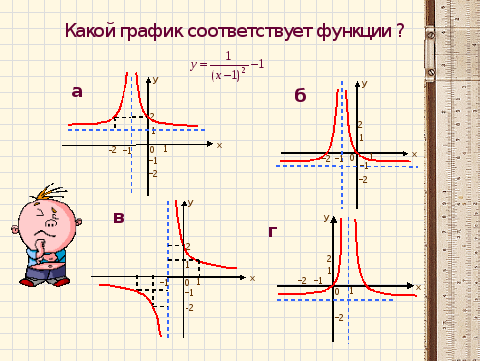
Это формула, показывает, что график функции
Учащиеся анализируют и сопоставляют графики, приходят к единому решению пары и в тетрадях заполняют табличку:
Проверяют выполненное задание и исправляют допущенные ошибки.
Учащиеся анализируют и сопоставляют графики, выполняя задание, в тестовых листах записывают получившееся из номеров графиков 9-значное число. |
Отложите на край стола (лицевой стороной вниз) тестовые бланки. После работы с новым материалом, мы продолжим работу с убранными листами.
3. Изучение нового материала. Обучающая беседа с элементами исследования и демонстрацией.
| Учитель | Доска | Ученик |
| Переходим к изучению нового материала. В тетрадях записываем тему урока «Взаимно – обратные функции».
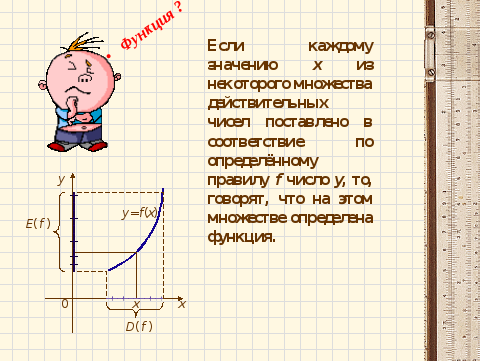
В процессе фронтальной беседы с классом, на конкретных примерах представленных на слайдах, повторяются понятия функции, области определения и области значения функции.
(Задание к каждому слайду можно прочитать в его заголовке)
Проверьте получившейся ответ по слайду.
Проверьте получившейся ответ по слайду
Проверьте получившейся ответ по слайду
Решим некоторую аналитическую задачу: Найти значение функции y=3x+1 в точке -2.
Рассмотрим похожую аналитическую задачу: Для функции y = - 7x + 3,5 найдите значение аргумента, если значение функции равно -11,2.
Решение задачи (без записи условия) оформить в тетрадях.
Как называются задачи, решением которых вы только что занимались по отношению друг к другу.
| Слайды 13-26:
|
Смотрит слайды, вспоминает определение понятия функции, области определения и множества значений. В соответствии с вышеназванными понятиями даёт обоснованный ответ на поставленный вопрос.
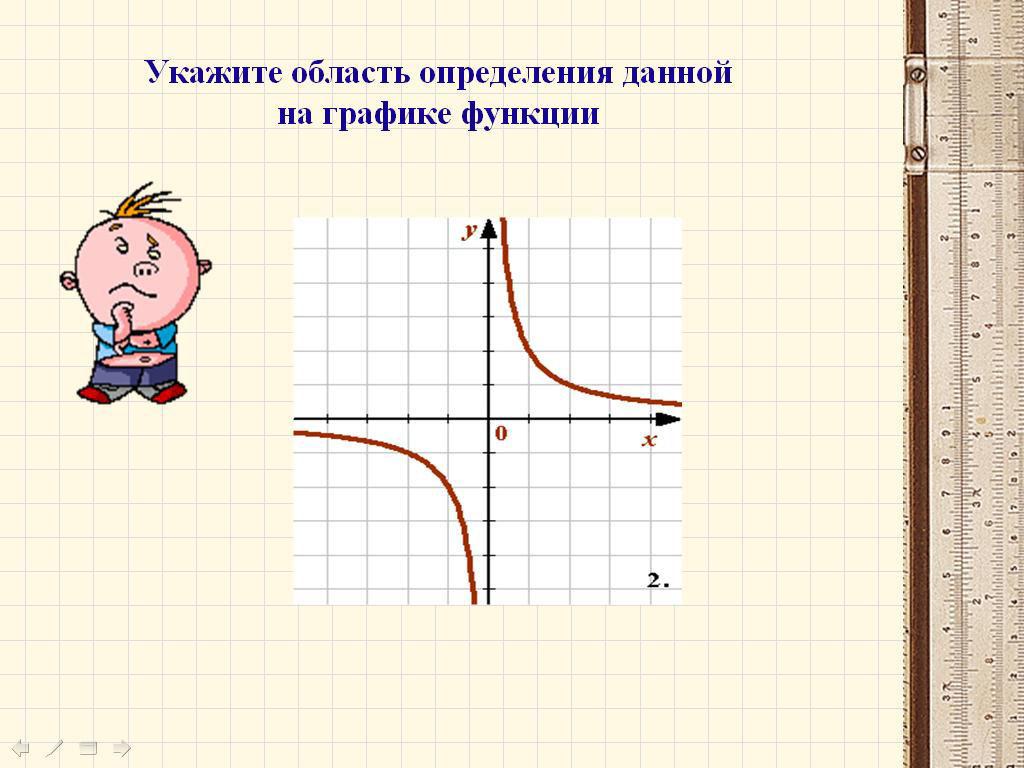
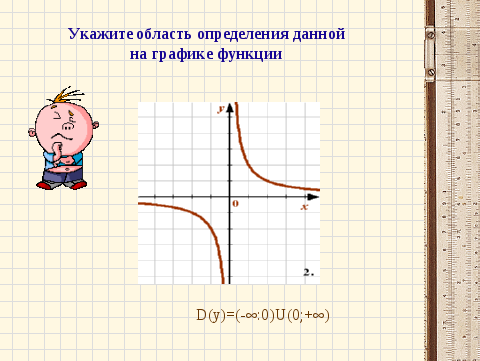
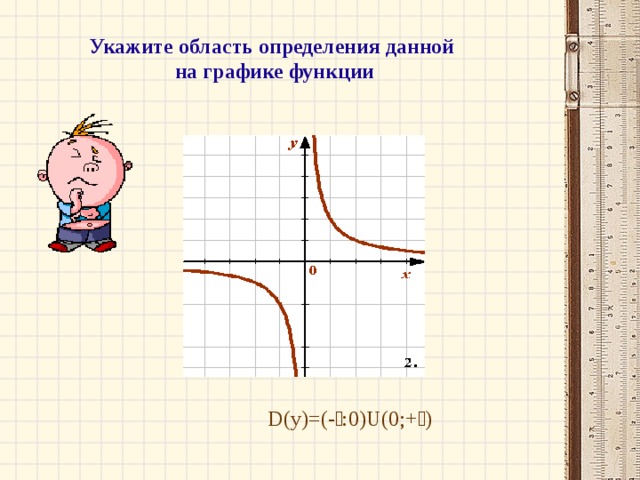
По графику видно, что данная функция определена при всех значениях независимой переменной, кроме нуля. Таким образом, областью определения данной функции будет множество значений аргумента:
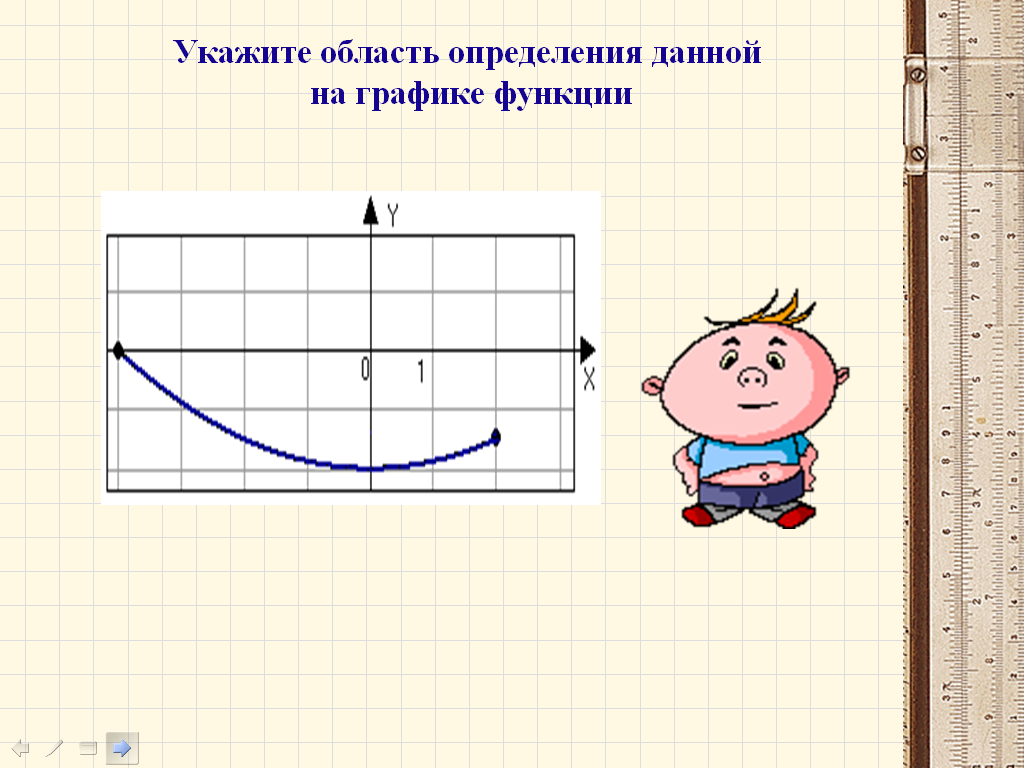
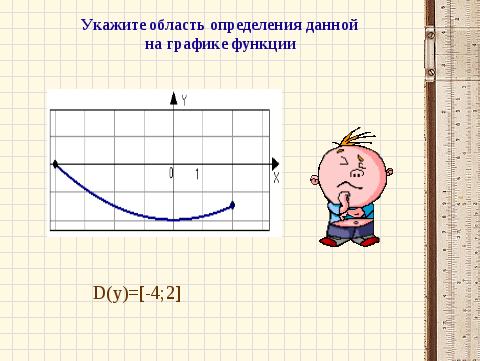
По графику видно, что данная функция задана для всех значений независимой переменной, на отрезке от -4 до 2, включая крайние точки.. Таким образом, областью определения данной функции и будет данный отрезок.
D(y)=[-4;2]
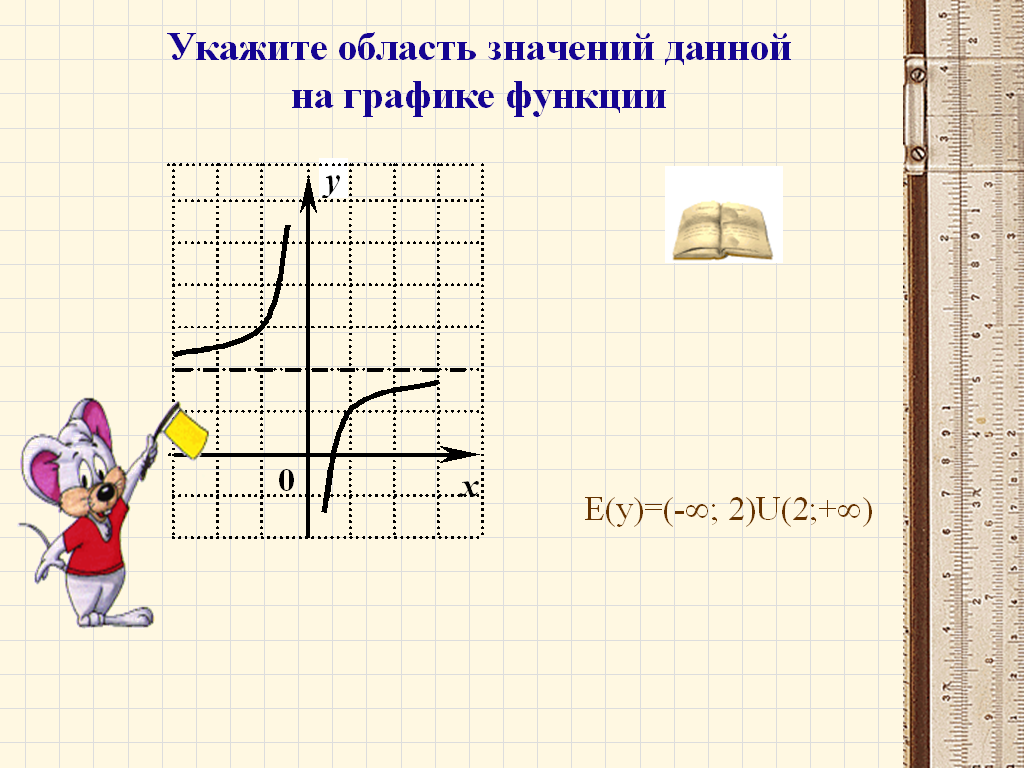
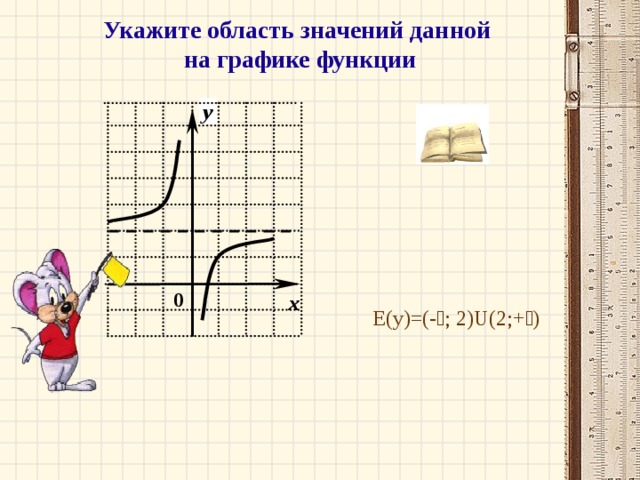
По графику видно, что данная функция определена при всех значениях независимой переменной, кроме нуля. Таким образом, областью определения данной функции будет множество значений аргумента:
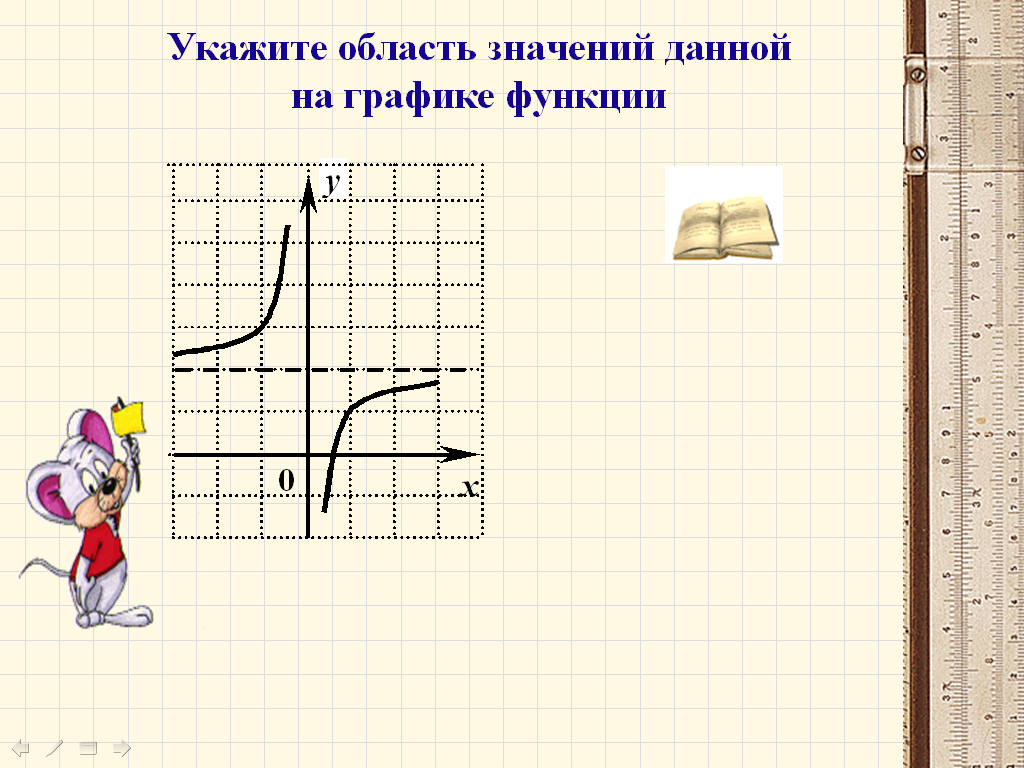
Е(y)=(-¥; 2)U(2;+¥)
Учащиеся решают и проговаривают решение задачи устно . После устного ответа одного из учащихся появляется решение на слайде.
Учащиеся самостоятельно решают задачу в тетрадях. После сверки ответа, решение появляется на слайде.
Данные задачи являются обратными друг для друга. Наприме: первая задача – прямая, а вторая – обратная. |
Мы разобрали два примера функций, когда каждому значению функции соответствует одно значение аргумента. Для таких функций можно выразить не только прямую, но и обратную зависимость, т.е. зависимость значений аргумента от значений функции.
Рассмотрим один из примеров такой зависимости – это зависимость скорости движения тела, брошенного вверх с некоторой начальной скоростью от времени движения.
| Учитель | Доска | Ученик |
| Переходит к следующему слайду с разбором вышеназванной задачи.
Такие функции называются обратимыми. Примеры обратимых функций и необратимых появляются на слайде. Какие из представленных формул задают обратимую, а какие - необратимую функции?
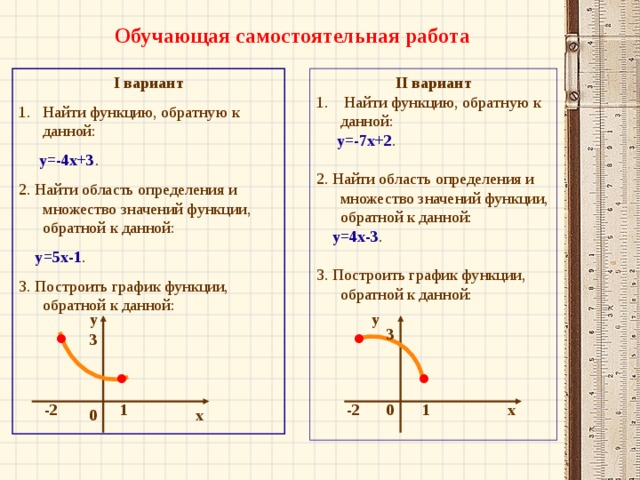
Итак, давайте выполним следующее задание: найти функцию, обратную для функции
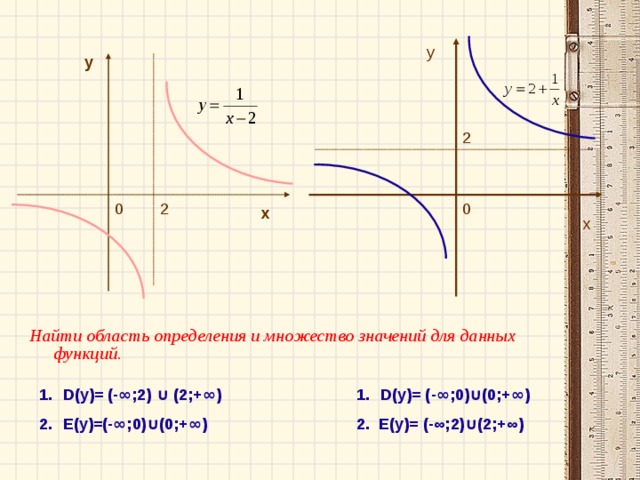
Найти область определения и множество значений данной и полученной функций.
Найдите теперь область определения и область значений этих взаимно-обратных функций. После того как они будут найдены, проверим их по слайду, представив себе их графическое изображение.
Как вы уже заметили, область определения обратной функции совпадает с множеством значений исходной функции и наоборот. Это одно из свойств взаимно-обратных функций.
Взаимно-обратные функции обладают и ещё одним свойством – свойством монотонности. Для интересующихся дома можно дома познакомиться с его доказательством, которое представлено на стр. 48 учебника. Это теорема 1.
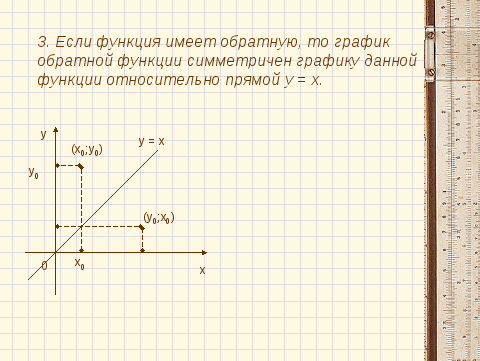
Теперь нам предстоит проследить как расположен график функции обратной данной.
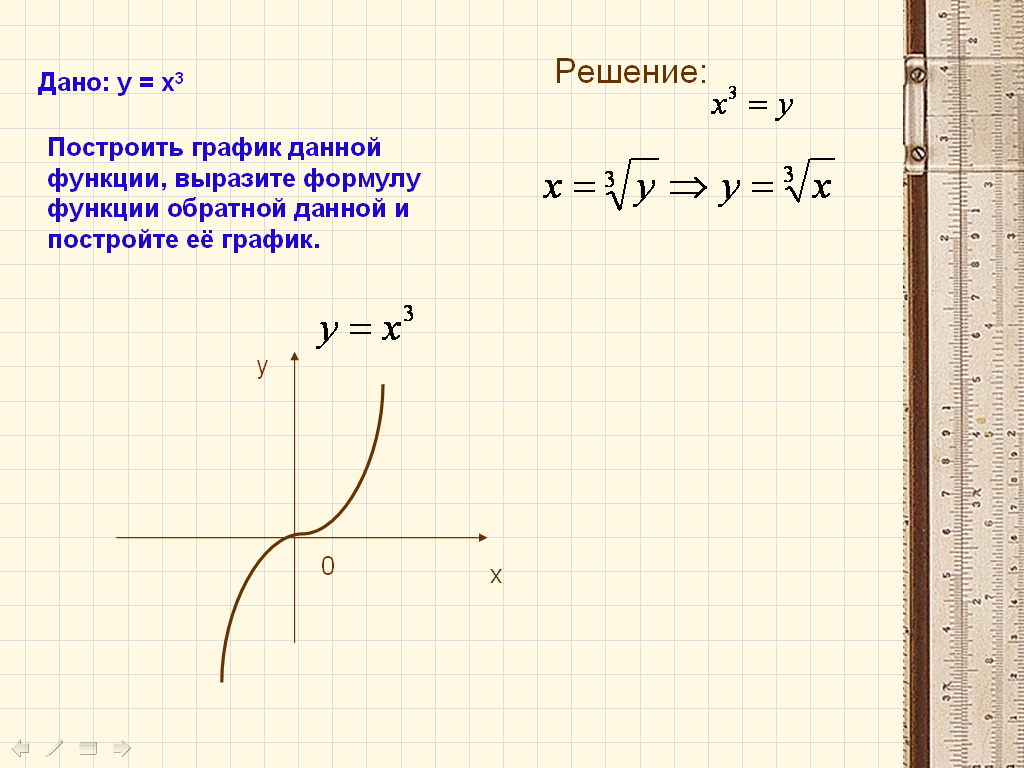
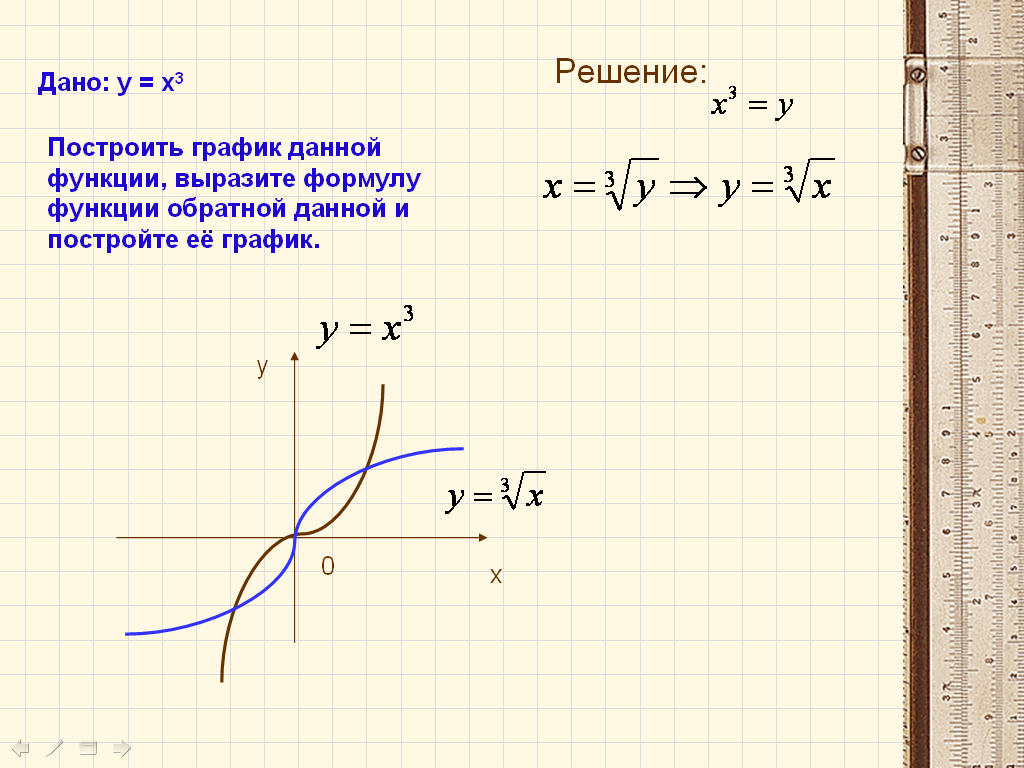
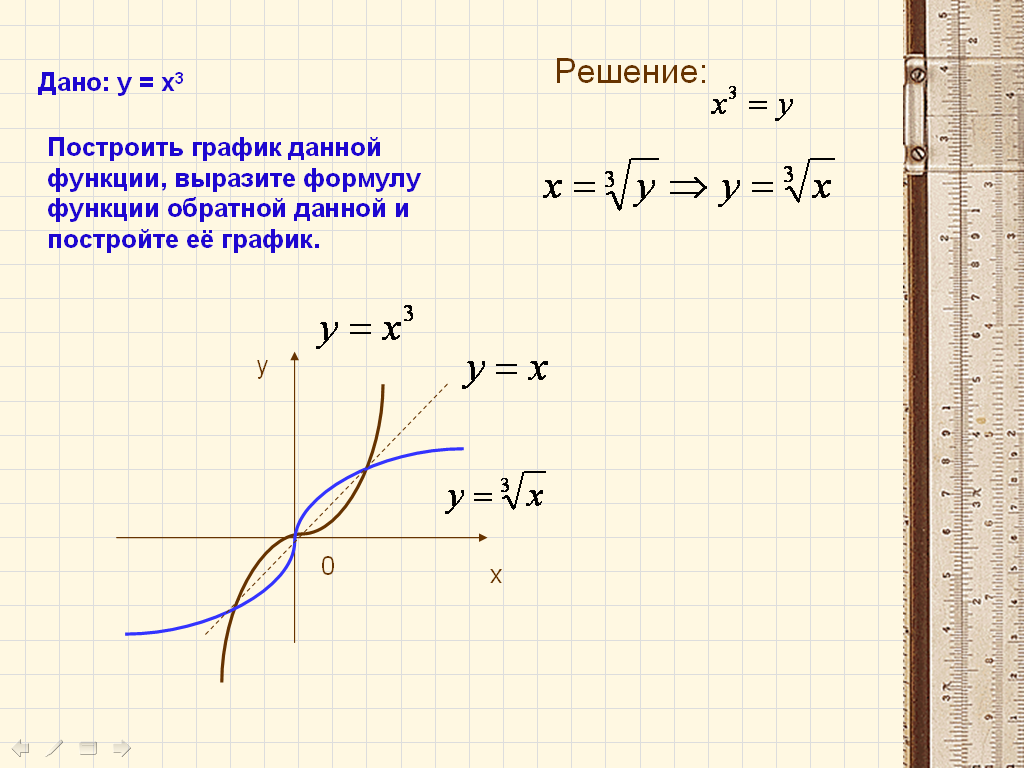
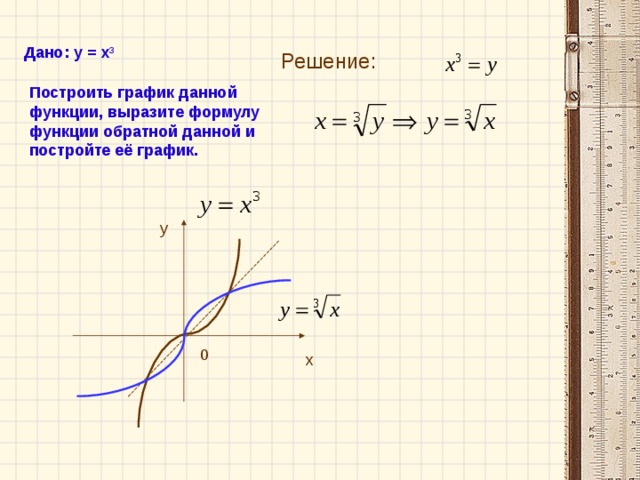
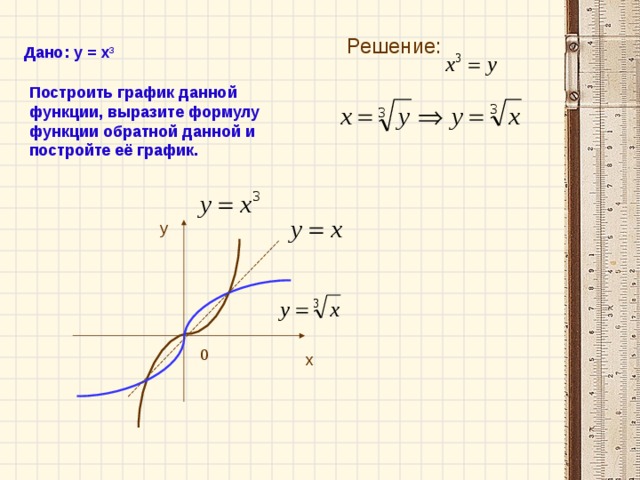
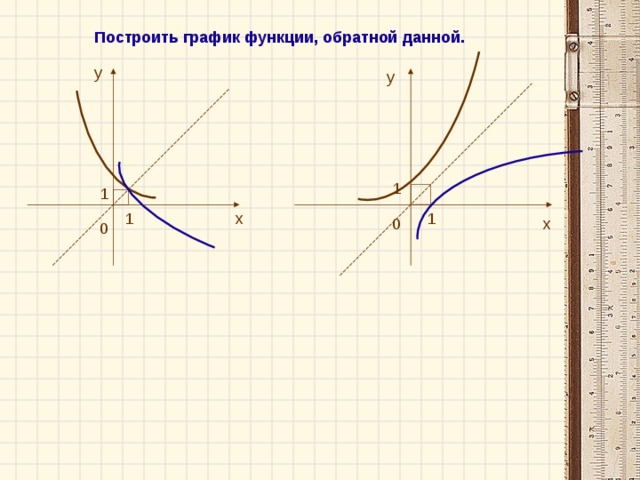
Задание. Работая в паре, постройте график функции у =x3. Выведите формулу обратной функции, изобразите её график.
Посмотрите внимательно на полученные графики. Что вы заметили?
Молодцы! Это третье свойство, с которым мы должны были с вами сегодня познакомиться. Итак:….
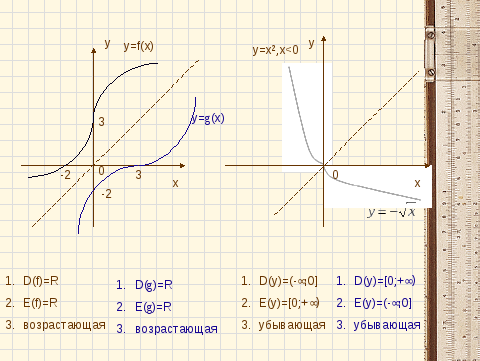
Давайте посмотрим на слайде ещё раз примеры построения графика функции g(x), обратной для данной функции f(x).
И графика функции y=x2 , заданного на множестве неположительных чисел и обратной для неё функции. |
| Один из учеников, проговаривая с места, решает задачу в тетради. Класс делает соответствующие записи в своих рабочих тетрадях. Одновременная анимация позволяет поэтапное появление записи на доске. Учащиеся исследуют поставленную перед ними проблему и дают обоснованный ответ, который затем проверяют на слайде. Учащиеся оформляют решение задачи в тетрадь. Решение с комментируемым управлением.
Для прямой функции:
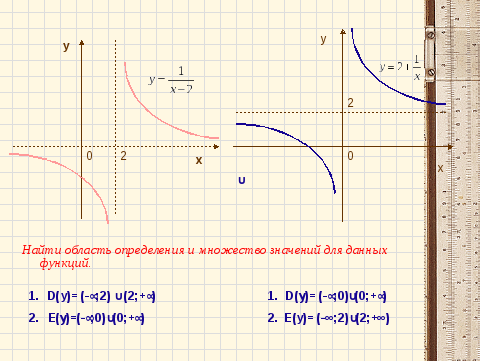
Область определения: D(у)= (-∞;2)
Множество значений: Е(у)=(-∞;0)
Для обратной функции:
Область определения: D(у)=(-∞;0)
Множество значений: Е(у)= (-∞;2)
Учащиеся в тетрадях выполняют задание и поэтапно сверяют его выполнение со слайдами. Решение идёт под комментируемым одним из учащихся управлением.
По чертежу видно, что построенные графики, симметричны относительно прямой y=x. |
4. Физкультминутка
Пришло время отдохнуть 2 минутки:
Для улучшения мозгового кровообращения :
И.п.- сидя на стуле. 1-2 – плавно наклонить голову назад, на счёт 3-4 – голову наклонить вперёд и вернуть в и.п, плечи не поднимать. Повторить 4-6 раз, темп медленный.
И.п.- сидя, руки на поясе. 1-поворот головы направо, 2 – и.п. 3 – поворот головы налево. 4 – и.п. Повторить 6-8 раз. Темп медленный.
И.п. – стоя или сидя, руки на поясе. 1 – махом левую руку занести через левое плечо, голову повернуть налево, 2 – и.п. 3-4 – то же выполнить правой рукой. Повторить 4-6 раз. Темп медленный.
Гимнастика для глаз
Быстро поморгать, закрыть глаза и посидеть спокойно, медленно считая до 5. повторить 4-5 раз.
Крепко зажмурить глаза (считать до 3), открыть их и посмотреть вдаль (считать до 5). Повторить 4—5 раз.
В среднем темпе проделать 3-4 круговых движений глазами в правую сторону, столько же в левую сторону. Расслабить глазные мышцы, посмотреть вдаль на счёт 1 – 6. Повторить 2-3 раза.
5. Закрепление знаний
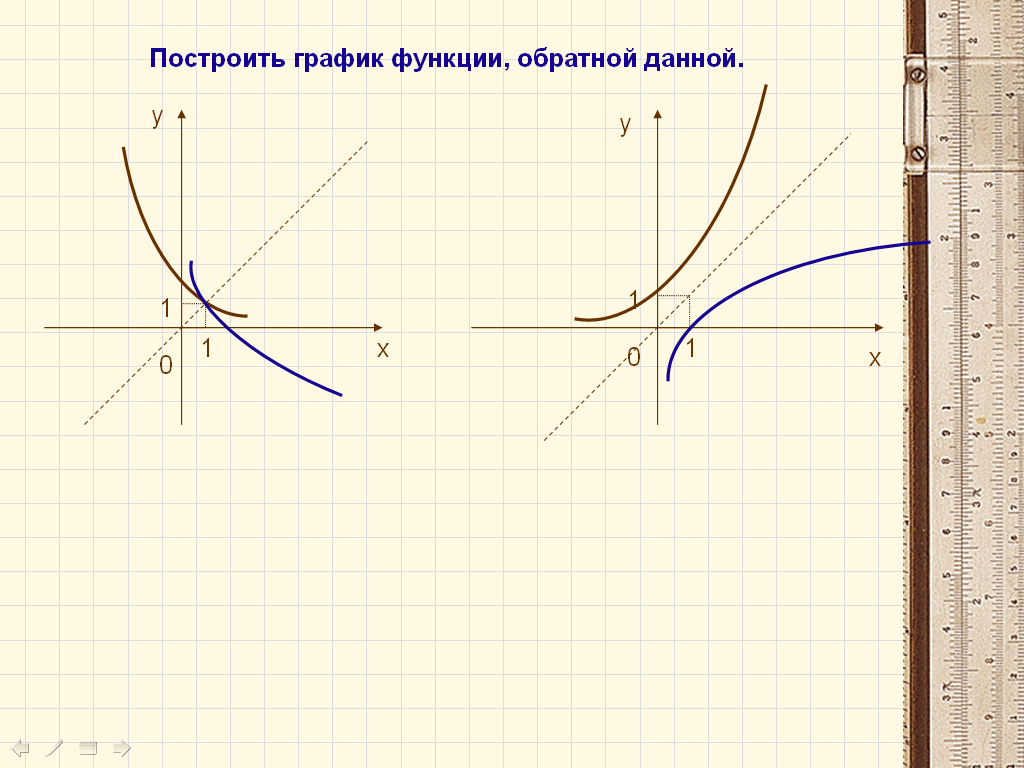
Продолжаем работу в парах. На столе лежат листы на которых изображены графики некоторых функций. Каждый из вас строит один из графиков, а затем передаёт соседу по парте для проверки. После окончания выполнения задания, проверки и взаимоконтроля, вы как всегда сможете проверить результат на соответствующем слайде..
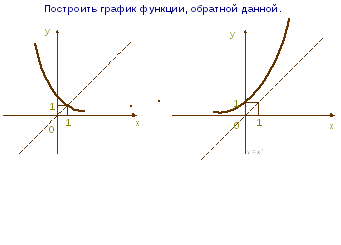
Проверим выполнение задания с помощью анимированного слайда.
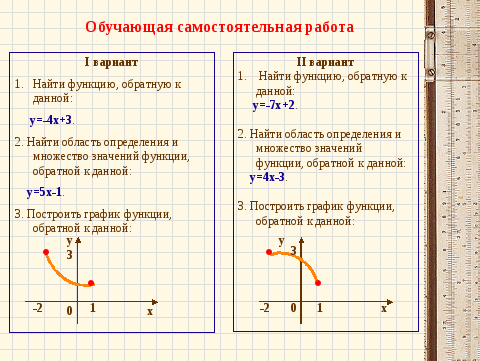
6. Контроль знаний.
В заключении урока вам предстоит выполнить небольшую обучающую самостоятельную работу, представленную на слайде.
Возьмите тестовые листы с ответами «Графического лото», и продолжите работу. В вашем распоряжении 5 минут.
Завершайте свою работу.
Поменяйтесь листами с соседом, приступаем к взаимопроверке.
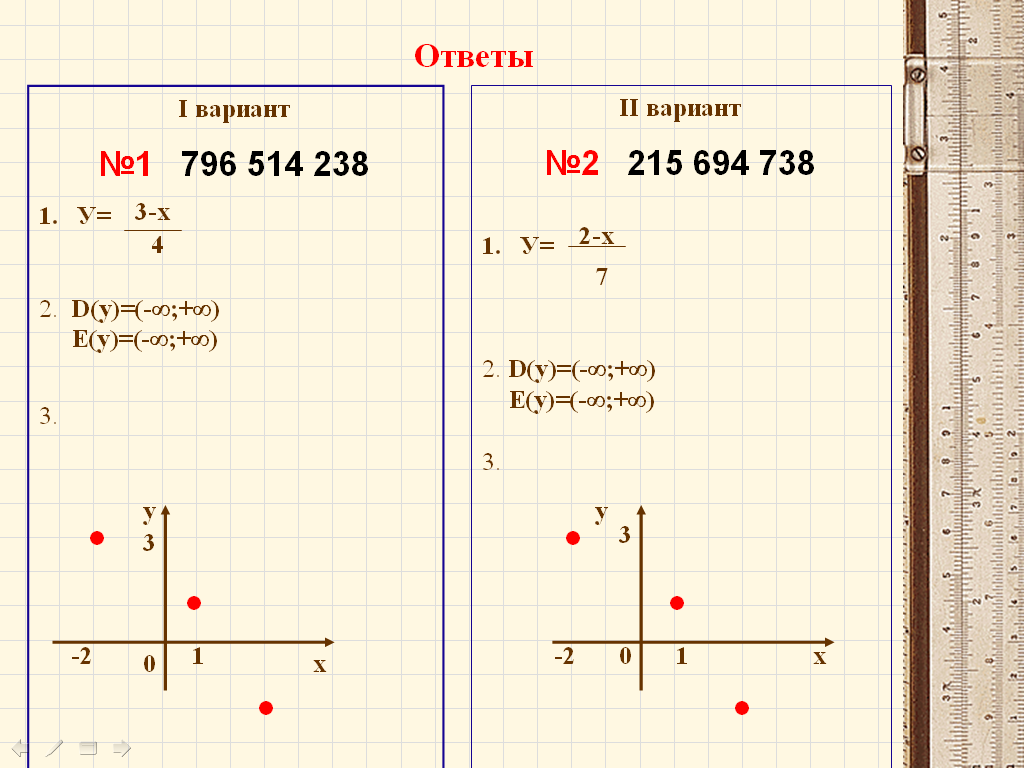
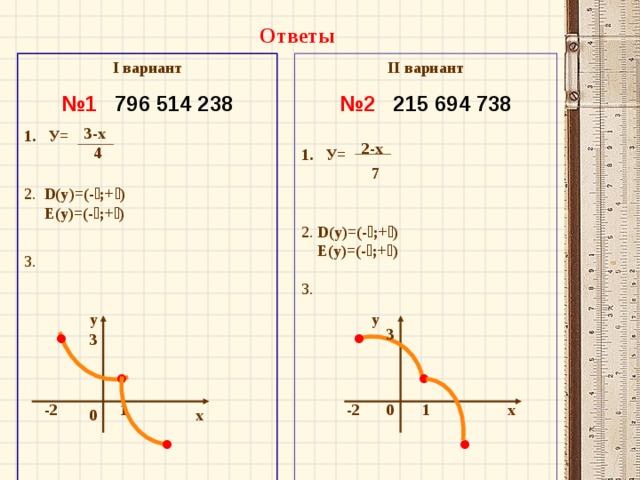
При проверке первого задания достаточно просто сверить получившееся число со слайдом.
Для проверки последующих заданий также можно воспользоваться слайдами.
Передайте листочки на первую парту.
6. Задание на дом: В дневниках запишите задание на следующий урок.

Рефлексивно-оценочный этап
Традиционно подводим итог урока. Пожалуйста, желающие могут сказать несколько слов.
Спасибо за урок!

 Получите свидетельство
Получите свидетельство Вход
Вход



 Математическая игра «Графическое лото»
Математическая игра «Графическое лото»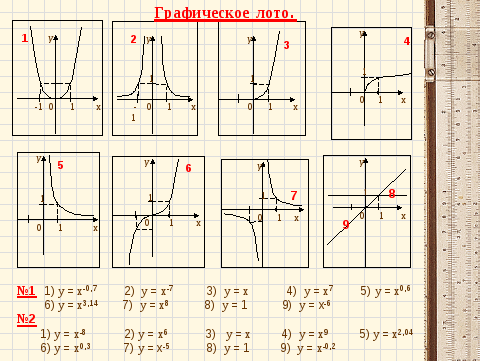












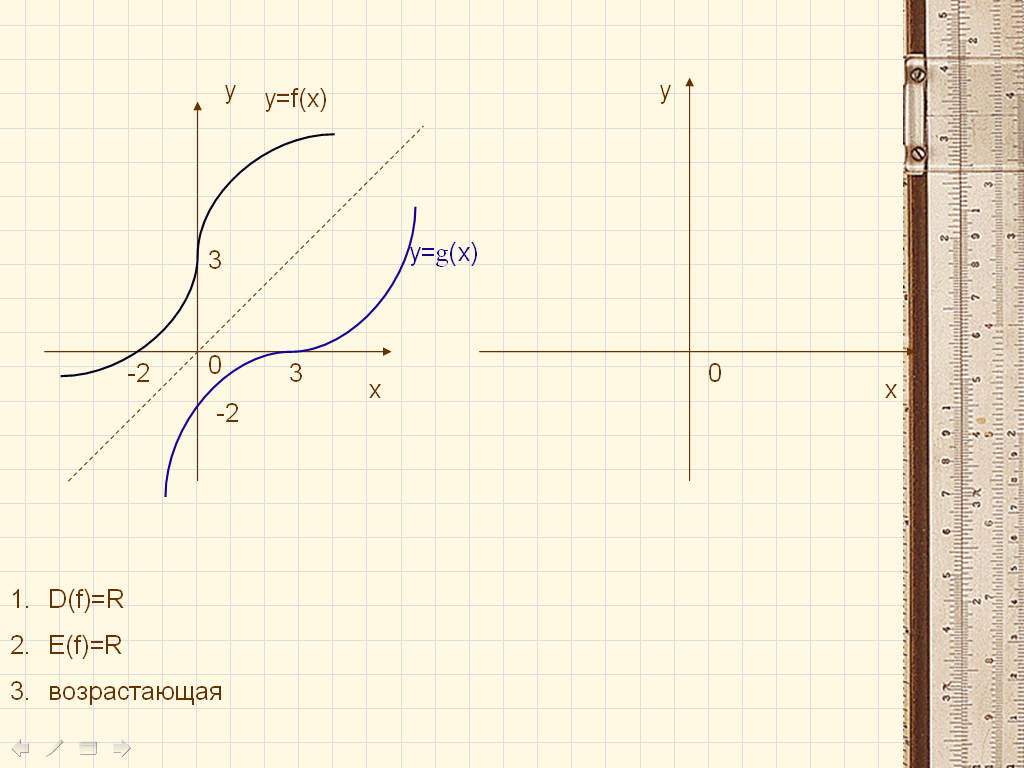




![Укажите область определения данной на графике функции D(y)= [-4;2]](https://fsd.videouroki.net/html/2018/09/20/v_5ba3f04b4a65c/img_v99719993_0_14.jpg)

















 Взаимно обратные функции (6.75 MB)
Взаимно обратные функции (6.75 MB)
 0
0 1856
1856 155
155 Нравится
0
Нравится
0



