Вписанная - описанная окружности

Геометрия 8 класс

Вписанная и описанная окружности

Выполнила: Василик Татьяна Тимофеевна, учитель математики МОУ ЦО «Открытие», г. Комсомольска-на-Амуре, Хабаровского края

5/4/20 05:55:04 AM

Определение

Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник – описанным около этой окружности

5/4/20 05:55:04 AM

Вписанная окружность

F

Е

.

O

M

N

5/4/20 05:55:04 AM

Теорема:

В любой треугольник можно вписать окружность.

С

Рассмотрим произвольный треугольник АВС и обозначим буквой О точку пересечения его биссектрис.

Проведем из точки О перпендикуляры ОК, ОL и ОМ соответственно к сторонам АВ, ВС и СА.

Так как точка О равноудалена от сторон ∆ АВС, то ОК=ОL=OM. Поэтому окружность с центром О и радиуса ОК проходит через точки К, L и М.

Стороны ∆ АВС касаются этой окружности в точках К, L и М, так как они перпендикулярны к радиусам ОК, OL и ОМ. Значит окружность с центром О радиуса ОК является вписанной в ∆АВС.

L

O

.

М

В

K

А

5/4/20 05:55:04 AM

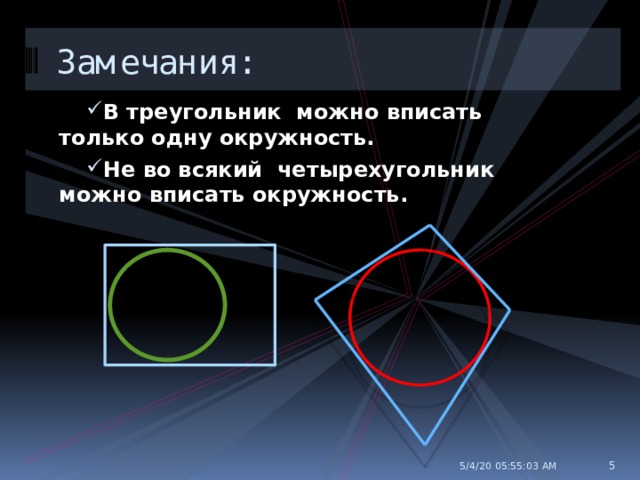
Замечания:

• В треугольник можно вписать только одну окружность.
• Не во всякий четырехугольник можно вписать окружность.

5/4/20 05:55:04 AM

•

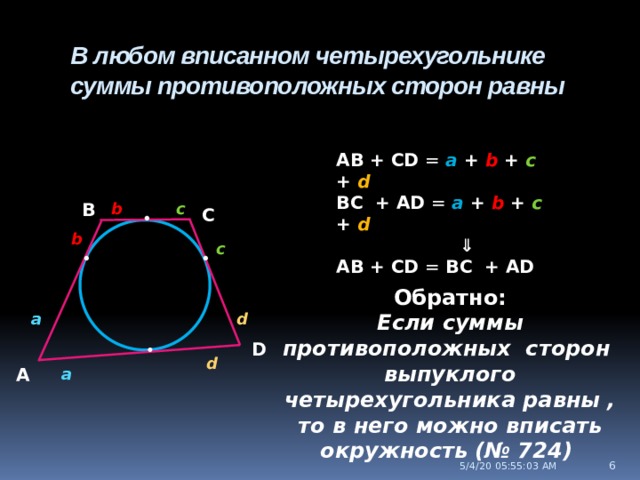
В любом вписанном четырехугольнике суммы противоположных сторон равны

AB + CD = a + b + c + d

BC + AD = a + b + c + d

⇓

AB + CD = BC + AD

b

c

В

С

•

b

c

•

•

Обратно:

Если суммы противоположных сторон выпуклого четырехугольника равны , то в него можно вписать окружность (№ 724)

d

a

D

d

a

А

5/4/20 05:55:04 AM

Описанная окружность

Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник - вписанным в эту окружность

5/4/20 05:55:04 AM

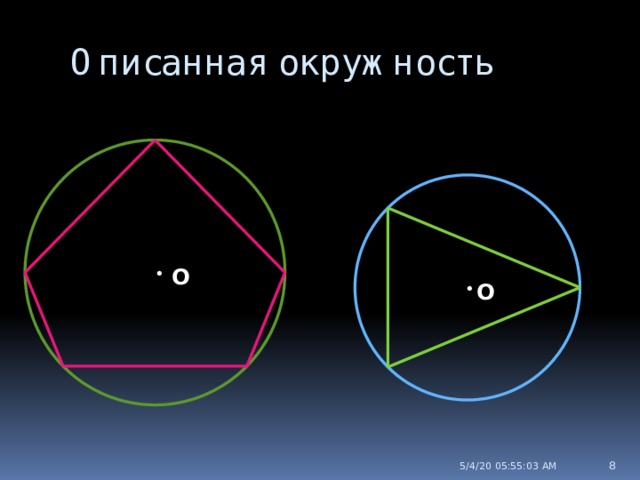
Описанная окружность

•

О

•

О

5/4/20 05:55:04 AM

Теорема:

Около любого треугольника можно описать окружность

Рассмотрим произвольный треугольник АВС.

Проведем серединные перпендикуляры к сторонам треугольника и точку их пересечения обозначим буквой О.

Проведем отрезки ОА, ОВ и ОС.

Так как точка О равноудалена от вершин треугольника АВС, то ОА = ОВ = ОС.

Окружность с центром О и радиуса ОА проходит через три вершины треугольника и, значит, является описанной около треугольника АВС.

В

•

А

О

С

5/4/20 05:55:04 AM

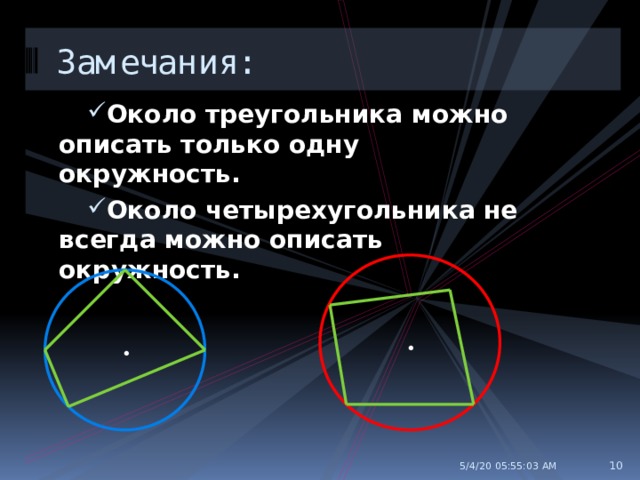
Замечания:

• Около треугольника можно описать только одну окружность.
• Около четырехугольника не всегда можно описать окружность.

•

•

5/4/20 05:55:04 AM

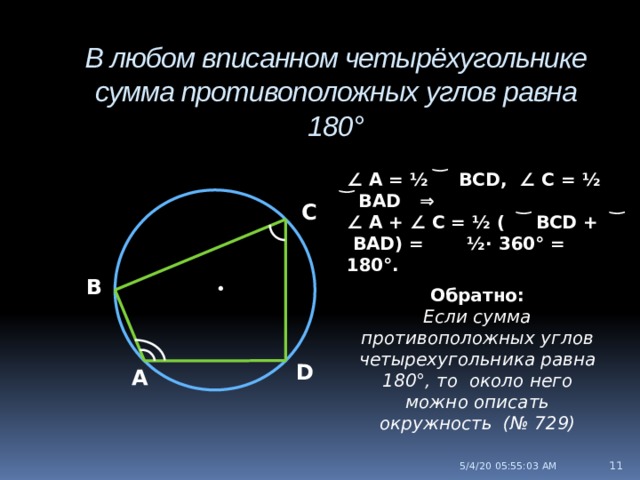
В любом вписанном четырёхугольнике сумма противоположных углов равна 180°

∠ А = ½ ͝ BCD, ∠ C = ½ ͝ BAD ⇒

∠ A + ∠ C = ½ ( ͝ BCD + ͝ BAD) = ½∙ 360° = 180°.

С

В

•

Обратно:

Если сумма противоположных углов четырехугольника равна 180°, то около него можно описать окружность (№ 729)

D

А

5/4/20 05:55:04 AM