Министерство образования Саратовской области
Саратовский институт повышения квалификации и переподготовки работников образования
Кафедра математического образования
Вписанная и описанная окружность.
Метод вспомогательной окружности.
Творческая работа
слушателя курсов повышения квалификации
по рабочей программе «Школьное математическое образование: организационные, содержательные и методические аспекты развития»
учителя математики МКОУ-ООШ с.Большая Журавка Аркадакского района Саратовской области
Юдина Александра Александровича
Руководитель
доцент кафедры
математического образования,
Корнеева А.О.
Саратов 2013
Содержание
Введение .Историческая справка……………………………………………3-4
Глава 1 Теоретико-методические аспекты изучения темы «Вписанная и описанная окружность. Метод вспомогательной окружности.» в школьном курсе математики………………………………………………………...……5-9
Глава 2 «Вписанная и описанная окружность. Метод вспомогательной
окружности.» ……………………………………………….…10-13
2.1 Задачи из ЕГЭ…………………………………………………………....14-19
2.2 Дополнительный меатериал………………………………………….…20-21
Список использованной литературы..……………………………………..….22
Интернет-ресурсы ……………………………………………………………..22
Историческая справка
Для первобытных людей важную роль играла форма окружающих их предметов. По форме и цвету они отличали съедобные грибы от несъедобных, пригодные для построек деревья и деревья, которые годятся лишь на дрова, вкусные орехи от горьких или ядовитых. Особенно вкусны орехи кокосовой пальмы. Эти орехи очень похожи на шар.
А добывая каменную соль или горный кварц, люди наталкивались на кристаллы, потом научились шлифовать их. Отшлифованные орудия позволили быстро срубить дерево, разрезать мясо, помогали лучше охотиться на зверей. Специальных названий для геометрических фигур тогда не было. Говорили: "Такой, как кокосовый орех”, (т. е. круглый), "такой, как соль” (т. е. имеющий форму куба). Некоторые формы фигур казались особо красивыми. И действительно, нельзя без восхищения смотреть на красоту кристаллов, цветов, фигур, имеющих правильную круглую форму.
Только в Древней Греции окружность и круг получили свои названия.
Круглые тела в древности заинтересовали человека. Так в Древнем Египте для постройки знаменитых египетских пирамид никаких технических сооружений еще не было. Даже шлифовать огромные каменные глыбы приходилось вручную, а перемещали их с помощью бревен круглой формы. Позже вместо бревен стали использовать их части – в виде колес, которые катились уже легче.
А теперь давайте поразмышляем о колесе.
В Древней Греции круг и окружность считали венцом совершенства. В каждой своей точке окружность устроена одинаковым образом, что позволяет ей двигаться самой по себе. Это свойство окружности стало толчком к возникновению колеса, так как ось и втулка колеса должны всё время быть в соприкосновении. К сожалению, неизвестен изобретатель колеса. Колесо – это чудо! Что же в нём особенного? – подумаете вы. Но это только на первый взгляд. Представьте себе на секунду, что вдруг случилась беда: на Земле исчезли все колёса!
Круг – колесо – прогресс (движение вперед)
Если остановится колесо, то остановится колесо Истории. Остановятся все виды транспорта, остановятся все часы и механизмы, фабрики и заводы. Не произойдет движения вперед.
Самые первые колеса были сделаны в Месопотамии (ныне Ирак) в 3500-
3000 гг. до н. э. и представляли собой гончарный круг и тележное колесо.
Не только в процессе работы люди знакомились с различными фигурами. Издавна они любили украшать себя, свою одежду, свое жилище. И многие, созданные давным-давно украшения, имели ту или иную форму.
Бусинки были шарообразными, браслеты и кольца имели форму окружности. Древние мастера научились придавать красивую форму бронзе, золоту, серебру, драгоценным камням. Художники, расписывавшие дворцы, тоже использовали окружность. Со времени изобретения гончарного круга люди научились делать круглую посуду – горшки, вазы, амфоры. Круглыми были и колонны, подпирающие здания. Самым важным среди круглых тел был шар.
Самая простая из всех кривых линий - окружность. Это одна из древнейших геометрических фигур. Философы древности придавали ей большое значение. Согласно Аристотелю, небесная материя, из которой состоят планеты и звезды, как самая совершенная, должна двигаться по самой совершенной линии - окружности. Сотни лет астрономы считали, что планеты двигаются по окружностям. Это ошибочное мнение было опровергнуто лишь в XVII веке учением Коперника, Галилея, Кеплера и Ньютона.
Теоретико-методические аспекты изучения темы «Вписанная и описанная окружность. Метод вспомогательной окружности»
в школьном курсе математики
Статистические данные анализа результатов проведения ЕГЭ говорят о том, что наименьший процент верных ответов традиционно дается учащимися на геометрические задачи. Задачи по планиметрии, включаемые в КИМы ЕГЭ, можно сгруппировать по следующим основным темам:
Треугольники.
Четырехугольники (параллелограмм и трапеция)
Окружности, вписанные в треугольник и описанные около треугольника.
Окружности, вписанные в четырехугольник и описанные около четырехугольника.
В КИМы включены 2 задачи по стереометрии. Разумеется, для успешного решения стереометрических задач учащиеся должны хорошо решать планиметрические задачи.
Как известно, решению геометрических задач в школе уделяется мало внимания. Тема “Вписанные и описанные окружности” изучается в конце 8 класса. И на решение задач отводится недостаточное количество часов. Совершенно очевидно, что нужна специальная подготовка. Для этих целей можно использовать элективный курс «Авторская программа элективного курса по геометрии "Решение планиметрических задач на вписанные и описанные окружности" для учащихся 9-х классов» (автор Валиева Сария Зиннатулловна, учитель математики) или элективный курс «Метод вспомогательной окружности» (геометрия; 12 часов; для предпрофильной подготовки учащихся 9 класса) Автор: учитель математики высшей категории муниципального общеобразовательного учреждения
«Гимназия № 1» г. Саратова Распарин Владимир Николаевич Рецензенты: доцент кафедры математического образования ГАОУ ДПО «СарИПКиПРО», к.ф.м.н. Корнеева А.О., кандидат педагогических наук, доцент кафедры математики и методики ее преподавания СГУ Т. А. Капитонова. 2010 год. С данным элективным курсом можно ознакомиться на сайте
http://www.slideshare.net/
Теперь перейдем непосредственно к теме «Вписанная и описанная окружность. Метод вспомогательной окружности»
Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник - описанным около этой окружности .
Вписанные и описанные окружности
1. Окружность и треугольники
биссектрис треугольника, ее радиус r вычисляется по формуле:
r = 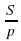 где S — площадь треугольника,
где S — площадь треугольника, 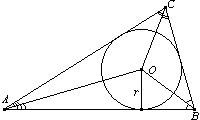
а 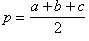 — полупериметр;
— полупериметр;
R = 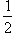
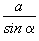 ,
,
R = 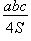 ;
;
здесь a, b, c — стороны треугольника, 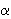 — угол, лежащий против стороны a, S — площадь треугольника;
— угол, лежащий против стороны a, S — площадь треугольника;
центр описанной и вписанной окружностей треугольника совпадают только в том случае, когда этот треугольник — правильный
Теорема 1: В любой треугольник можно вписать окружность
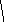


 К
К
O
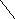
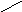 А В
А В
М
C L
Доказательство: Рассмотрим произвольный треугольник АВС и обозначим точкой О точку пересечения ее биссектрис. Проведем из точки О перпендикуляры ОК, OL, и OM соответственно к сторонам АВ, ВС, и АС.
Так как точка О равноудалена от сторон треугольника АВС, то OK=OL=OM. Поэтому окружность с центром О и радиусом ОК проходит через точки K, L и М. Стороны треугольника АВС касаются этой окружности в точках K, L и M, так как они перпендикулярны к радиусам OK,OL и OM. Значит, окружность с центром в О радиуса ОК является вписанной в треугольник АВС. Теорема доказана.
Замечания: В треугольник можно вписать окружность и притом только одну.
![]()

 Теорема 2: Около любого треугольника можно описать окружность
Теорема 2: Около любого треугольника можно описать окружность
О
С
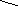
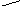
![]()


 А В
А В
Доказательство: Рассмотрим произвольный треугольник ABC. Обозначим буквой O точку пересечения серединных перпендикуляров к его сторонам и проведем отрезки OA, OB и OC. Так как точка O равноудалена от вершин треугольника ABC, то AO=OB=OC. Поэтому окружность с центром O радиуса OA проходит через все три вершины треугольника и, значит, является описанной около треугольника ABC.
Теорема доказана.
2.Окружность и четырехугольники
В отличие от треугольника не во всякий четырехугольник можно вписать
окружность, и около четырехугольника не всегда можноописать окружность. Если же в четырехугольник можно вписать окружность, то его стороны и углы обладают следующим замечательным свойством:
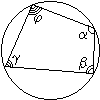

α+ γ = β +φ=1800
 a + c = b + d;
a + c = b + d;
около параллелограмма можно описать окружность тогда и только тогда, когда он является прямоугольником;
около трапеции можно описать окружность тогда и только тогда, когда эта трапеция — равнобедренная; центр окружности лежит на пересечении оси симметрии трапеции с серединным перпендикуляром к боковой стороне;
в параллелограмм можно вписать окружность тогда и только тогда, когда он является ромбом.
Метод вспомогательной окружности
1.Вписанные и описанные многоугольники
При решении планиметрических задач, когда требуется установить равенство некоторых углов, нередко полезно около треугольника или четырёхугольника описать окружность. Это позволяет использовать теорему о вписанном угле и её следствия.
Как известно, около всякого треугольника можно описать окружность, и притом только одну. При определённом условии окружность можно описать и около четырёхугольника. Если четырёхугольник ABCD вписан в окружность, то сумма его противоположных углов равна 1800, а углы ABD и ACD, опирающиеся на одну и ту же дугу, равны. Верно и обратное предположение.

 D
D

 C
C


![]()
A B
Вспомогательные построения позволяют сократить и упростить вычисления. Всегда интересно задачу на построение решить геометрически, придумать подходящее вспомогательное построение. В случае неудачи стоит перейти к вычислениям, выразить через данные элементы некоторые другие элементы треугольника и посмотреть, что подскажут полученные формулы.
Свойства дополнительных треугольников позволяют весьма просто решить некоторые геометрические задачи. Например, задачи на вычисление элементов треугольника, когда легче найти зависимость между элементами дополнительного треугольника, а также задачи на построение, если известны элементы треугольника, дополнительного к искомому.
Для решения таких задач используются геометрические преобразования, которые приводят к построению вспомогательных фигур. Это может быть вспомогательная окружность, которую можно вписать и описать около треугольника, четырёхугольника или многоугольника.
Итак, при решении задач можно воспользоваться следующими утверждениями:
Около всякого треугольника можно описать окружность, и притом только одну.
Если ABCD-выпуклый четырёхугольник и сумма его противоположных углов равна 180о, то ABCD можно вписать в окружность.
Точки В и С лежат по одну сторону от прямой AD и ABD=ACD (см. рисунок).
2.Ключевые задачи, решаемые методом вспомогательной окружности
Задача 1
В остроугольном треугольнике проведены высоты AP, BQ и CR. Доказать, что ABQ=APR.
Решение
Пусть Н – точка пересечения высот треугольника. Так как AРB и СРВ прямые, то около четырехугольника ВРНR можно описать окружность, приняв ВН за диаметр. Построив окружность, замечаем равенство углов ABQ=APR, как вписанных в окружность и опирающихся на одну и ту же дугу.
Таким образом, построение вспомогательной окружности позволило использовать теорему о вписанных углах и благодаря этому установить связь между указанными в задаче углами.
В случае, если В треугольника АВС тупой, равенство ABQ=APR не сохраняется.
Задача 2
Из произвольной точки М катета ВС прямоугольного треугольника АВС опущен на гипотенузу АВ перпендикуляр МN. Доказать, что MAN=MCN.
Решение
Рассмотрим четырехугольник ACMN - С и N равны по 90 градусов, а этого необходимо и достаточно для того, чтобы описать около четырехугольника окружность. Сразу замечаем, что искомые углы MAN и MCN опираются на одну и ту же дугу, следовательно, они равны.
Задача 3
Доказать, что прямая, соединяющая вершину прямого угла прямоугольного треугольника с центром квадрата, построенного внешне на гипотенузе, делит прямой угол треугольника пополам.
Решение
Проведем внутри квадрата диагонали. По свойству в точке пересечения диагонали делятся пополам (AD=CD). Рассмотрим четырехугольник ABCD – угол В и угол D прямые, значит около четырехугольника можно описать окружность.
В окружности две хорды (AD и CD) равны, значит и равны стягиваемые ими дуги. На равные дуги опираются вписанные углы АВD и CBD, значит, эти углы равны.
Задача 4
Доказать, что квадрат биссектрисы треугольника равен разности между произведением заключающих ее сторон и произведением отрезков третьей стороны, на которые она делится биссектрисой.
Решение
Около треугольника АВС опишем окружность и продолжим биссектрису CD треугольника до встречи с окружностью в точке Е. Пусть ВС=а, АС=b, AD=m, DB=n, CD=l, DE=x.
По условию ACE=BCE, кроме того, AЕС=АВС, как вписанные углы, опирающиеся на одну и ту же дугу. Следовательно, треугольники АСЕ и BCD подобны и справедливо равенство

Откуда l2 = ab – lx. Хорды АВ и СЕ пересекаются в точке D. Поэтому выполняется равенство lx = mn.
Следовательно l2 = ab – mn.
Задания из ЕГЭ
Правильные многоугольники: радиус вписанной и описанной окружности. Задание В6
-
Для того, чтобы научиться решать задачи из задания В6 на нахождение радиуса окружности, вписанной в правильный многоугольник, или описанной около него, не нужно запоминать большое количество формул. Нужно только вспомнить, как соотносятся стороны и углы в прямоугольном треугольнике.
И применить эти знания в немного другой ситуации.
Окружность называется описанной около многоугольника, если она проходит через все его вершины. Центр описанной окружности лежит в точке пересечения серединных перпендикуляров, проведенных к сторонам многоугольника.
Окружность называется вписанной в многоугольник, если она касается всех сторон многоугольника. Центр вписанной окружности лежит в точке пересечения биссектрис углов многоугольника.
В правильном многоугольнике центр вписанной и описанной окружности совпадают.
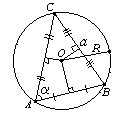
Посмотрим, как соотносятся между собой радиусы вписанной и описанной окружности и сторона правильного многоугольника.Рассмотрим фрагмент правильного многоугольника:
Здесь
АВ – сторона правильного треугольника
ОК – радиус вписанной окружности
ОВ, ОА – радиусы описанной окружности
Очевидно, что треугольник АОВ – равнобедренный, поэтому ОК является высотой, биссектрисой и медианой.
Рассмотрим треугольник ОКВ. С его помощью мы найдем, как соотносятся между собой сторона правильного многоугольника, радиус вписанной и описанной окружности.
Угол AOB=  , где n- количество сторон многоугольника. Тогда угол
, где n- количество сторон многоугольника. Тогда угол  - то есть его величину мы знаем всегда.
- то есть его величину мы знаем всегда.
Мы видим, что:
радиус вписанной окружности r – является прилежащим катетом прямоугольного треугольника ОКВ
половина стороны многоугольника а/2 является противолежащим катетом прямоугольного треугольника ОКВ
радиус описанной окружности R является гипотенузой прямоугольного треугольника ОКВ
Тогда:

Решим несколько задач из Открытого банка заданий для подготовки к ЕГЭ по математике:
1. Задание B6 (№ 27944)
Около окружности, радиус которой равен r= , описан квадрат. Найдите радиус окружности, описанной около этого квадрата.Проведем радиусы вписанной и описанной окружности и рассмотрим наш «волшебный» прямоугольный треугольник:
, описан квадрат. Найдите радиус окружности, описанной около этого квадрата.Проведем радиусы вписанной и описанной окружности и рассмотрим наш «волшебный» прямоугольный треугольник:
По условию  , надо найти
, надо найти 
Тогда
Ответ: 4
2. Задание B6 (№ 27929)
Периметр правильного шестиугольника равен 72. Найдите диаметр описанной окружности.
В этой задаче мы пойдем немного другим путем, и расмотрим треугольник АОВ:
Угол АОВ= 0
0
Найдем сторону шестиугольника. Так как все стороны правильного шестиугольника равны, P=6AB=72. Отсюда АВ=12
Треугольник АОВ равнобедренный с углом 600, а, значит, равносторонний. Следовательно, R=AB=12 и D=2R=24
Ответ: 24.
Запомните: в правильном шестиугольнике сторона равна радиусу описанной окружности.
3. Задание B6 (№ 27917)
Найдите радиус окружности, вписанной в правильный шестиугольник со стороной 
![]() .
.
Рассмотрим треугольник ВОК:
Ответ: 1,5
4. Задание B6 (№ 27909)
Сторона правильного треугольника равна 
![]() . Найдите радиус окружности, вписанной в этот треугольник.
. Найдите радиус окружности, вписанной в этот треугольник.
Рассмотрим треугольник ВОК:
Ответ: 0,5
Дополнительный материал
Вписанные и описанные треугольники.
125. Доказать, что во всяком треугольнике биссектриса лежит между медианой и высотой, проведёнными из той же вершины.
126. Площадь треугольника равна произведению его полупериметра на радиус вписанной в него окружности. Доказать.
127. Из вершины прямого угла треугольника проведены лучи через центры вписанной в треугольник и описанной около него окружностей. Угол между этими лучами равен 7°. Вычислить острые углы треугольника.
128. Радиус окружности, описанной около прямоугольного треугольника ABC
( / С = 90°), равен R, радиус окружности, вписанной в этот треугольник, равен r:
а) выразить R + r, R — r, Rr через катеты а и b треугольника;
б) построить прямоугольный треугольник по заданным R и r.
Указание. Выразить через R и rгипотенузу треугольника и сумму его катетов. Далее смотри задачу № 18 дополнительного материала.
129. Вершина А остроугольного треугольника ABC соединена отрезком с центром О описанного около треугольника круга. Из вершины Aпроведена высота AD. Доказать, что / BAD = / ОАС.
130. Точка М — переменная точка отрезка АВ, середина которого обозначена О. На отрезках AM в MB как на гипотенузах построены равнобедренные прямоугольные треугольники АСМ и MDB.
а) Найдите геометрическое место точек С и D и точку пересечения этих геометрических мест — точку Р.
б) Докажите, что прямая РМ делит отрезок CD пополам.
в) Найдите геометрическое место центров окружностей, описанных около треугольника АМС.
Вписанные и описанные многоугольники.
131. Биссектрисы углов любого четырёхугольника образуют четырёхугольник, около которого можно описать окружность. Доказать.
132. Через середину дуги АВ окружности проходят две произвольные прямые, пересекающие окружность в точках F и С и хорду АВ в точках D и Е соответственно. Доказать, что точки F, С, D иЕ лежат на одной окружности.
См. задачу № 85 дополнительного материала.
133. В треугольнике ABC проведены высоты BB1 и СС1.Точка их пересечения обозначена К.Доказать, что точки A, B1, К, C1 лежат на одной окружности.
134. Во всяком треугольнике точки, симметричные точке пересечения высот относительно трёх сторон треугольника, лежат на окружности, описанной около этого треугольника. Доказать.
135. В равнобедренной трапеции, описанной около круга, квадрат высоты равен произведению её оснований. Доказать.
Список использованных источников
1.Книги
1.1 книга, меньше трех авторов
Савельев И.В. Курс общей физики. Т.1 Механика: Учебное пособие. – М.: Наука, 1982. – 432 с.
1.2 книга под редакцией
Освежающий курс лекций «Актуальные проблемы анестезиологии и реаниматологии/ Под ред. Э.В. Недашковского. – Архангельск: Высшая школа, 2002. – 340 с.
1.3 книга, авторов больше трех
Геометрия 7-9 класс /Л.Атанасян, В.И. Николаев, В.М. Сваркин и др. – Киев: Наукова думка, 1983. – 270 с.
2.3 статья из сборника
Иваницкий Г.Р. Донорская кровь и её альтернативы // Перфторорганические соединения в биологии и медицине. Сб. науч. тр. – Пущино: Изд-во «Сфера», 1999. – С. 5-20.
3.Интернетресурсы
1. Из истории окружности и круга http://12kurgan.ucoz.ru/
http://school.xvatit.com/
2.Вписанная и описанная окружность http://www.univer.omsk.su/omsk/Edu/Rusanova/circles.htm
http://www.slideshare.net/
Дополнительный материал
http://oldskola1.narod.ru/NiktinZ/d14.htm или НН Никитин ГГ Маслова сборник задач по геометрии
Задания из ЕГЭ http://ege-ok.ru/
Геометрический портал http://www.neive.by.ru/
Графики функций http://graphfunk.narod.ru
ЕГЭ по математике: подготовка к тестированию http://www.uztest.ru/
12


 Получите свидетельство
Получите свидетельство Вход
Вход



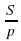 где S — площадь треугольника,
где S — площадь треугольника, 
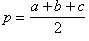 — полупериметр;
— полупериметр;


 К
К 
 А В
А В
 Теорема 2: Около любого треугольника можно описать окружность
Теорема 2: Около любого треугольника можно описать окружность 


 А В
А В 









 Творческая работа по математике "Вписанная и описанная окружность. Метод вспомогательной окружности" (0.25 MB)
Творческая работа по математике "Вписанная и описанная окружность. Метод вспомогательной окружности" (0.25 MB)
 0
0 3094
3094 250
250 Нравится
0
Нравится
0


