
16.10
Возрастание и убывание функций. Экстремумы.
Автор: Спирина Ирина Марксовна, учитель математики, I категории.
МКОУ «Яланская СОШ»
![График функции, определенной на отрезке [-1;10]. Эта функция возрастает на отрезках [-1;3] и [4;5], и убывает на отрезках [3;4] и [5,10].](https://fsd.videouroki.net/html/2013/10/15/98666469/img1.jpg)
График функции, определенной на отрезке [-1;10]. Эта функция возрастает на отрезках [-1;3] и [4;5], и убывает на отрезках [3;4] и [5,10].
у
у=х 2
х
0
 x 1 , выполнено неравенство f(x 2 ) f(x 1 ). " width="640"
x 1 , выполнено неравенство f(x 2 ) f(x 1 ). " width="640"
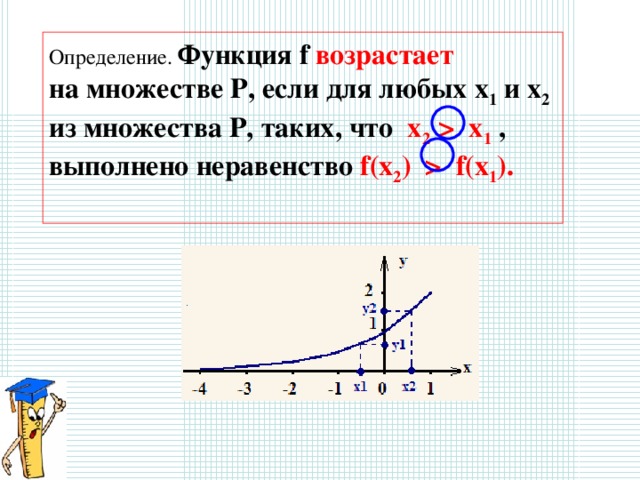
Определение. Функция f возрастает
на множестве P, если для любых x 1 и x 2
из множества P, таких, что x 2 x 1 ,
выполнено неравенство f(x 2 ) f(x 1 ).
 x 1 , выполнено неравенство f(x 2 ) 1 ). " width="640"
x 1 , выполнено неравенство f(x 2 ) 1 ). " width="640"
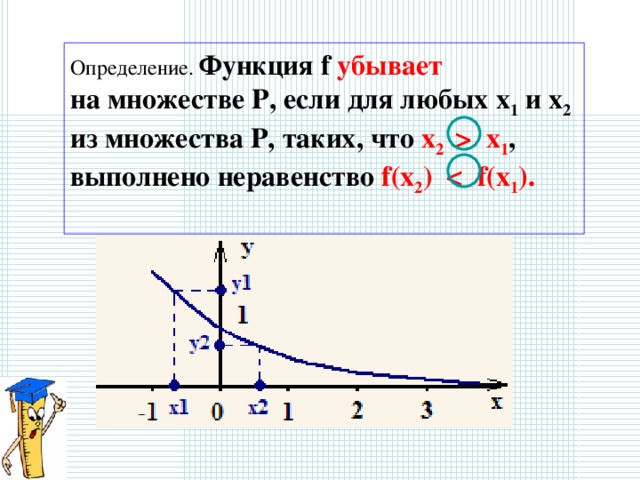
Определение. Функция f убывает
на множестве P, если для любых x 1 и x 2
из множества P, таких, что х 2 x 1 ,
выполнено неравенство f(x 2 ) 1 ).

Иначе говоря, функция f называется
возрастающей на множестве P,
если большему значению аргумента
из этого множества соответствует
большее значение функции.
Функция f называется убывающей
на множестве P, если большему
значению аргумента соответствует
меньшее значение функции.
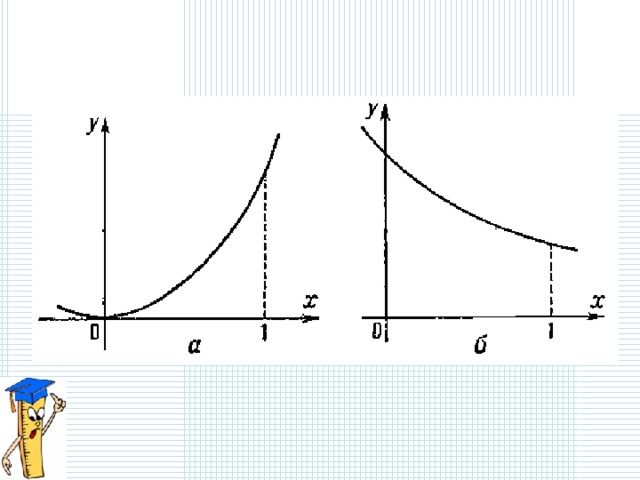
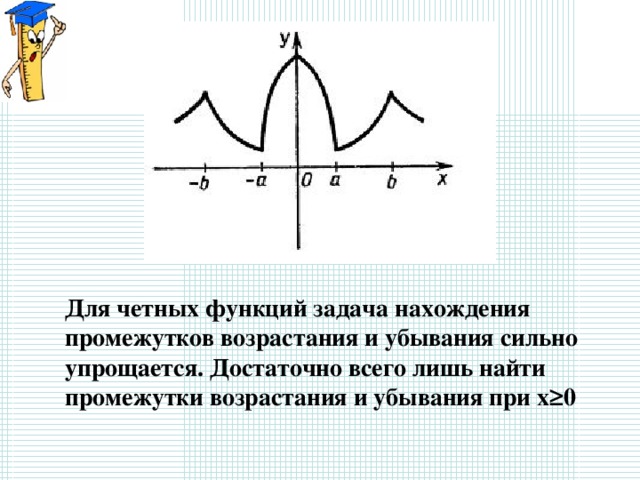
Для четных функций задача нахождения
промежутков возрастания и убывания сильно
упрощается. Достаточно всего лишь найти
промежутки возрастания и убывания при x ≥ 0

Возрастание и убывание функции синус
y = sin x
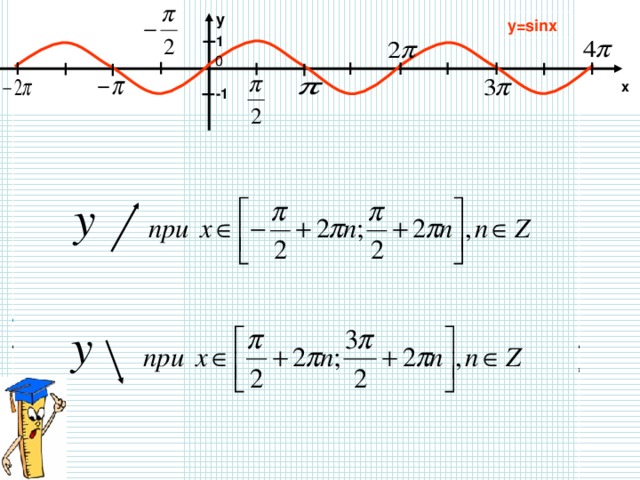
y
y = sinx
1
0
x
-1
y
y=cosx
1
0
x
-1

y
y = sinx
Возрастание и убывание функции косинус
1
x
-1
y = cos x
y
y=cosx
1
0
x
-1
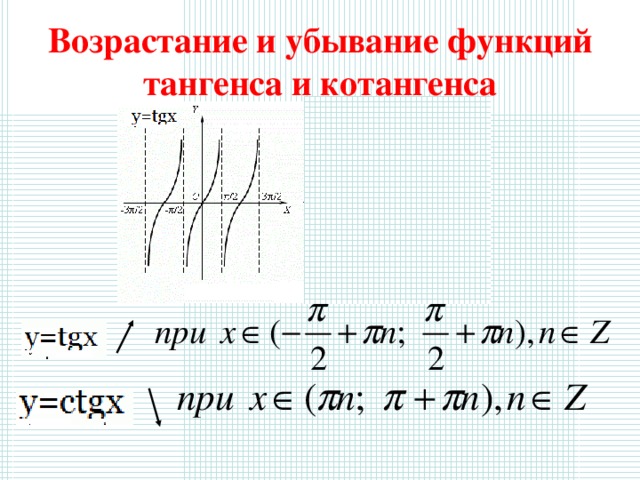
Возрастание и убывание функций тангенса и котангенса

Экстремумы.
Окрестность
Окрестность точки
а
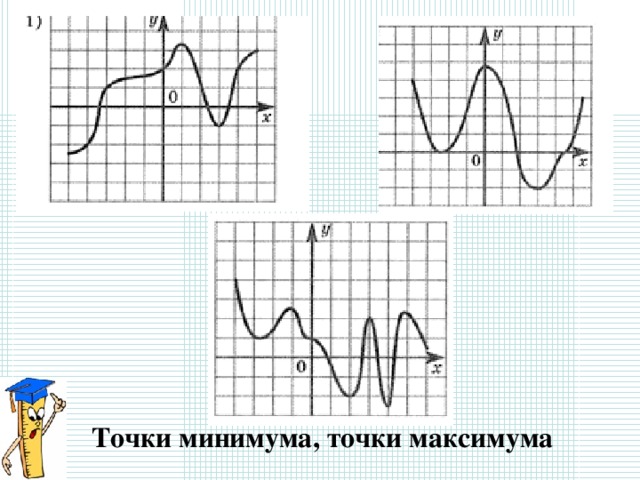
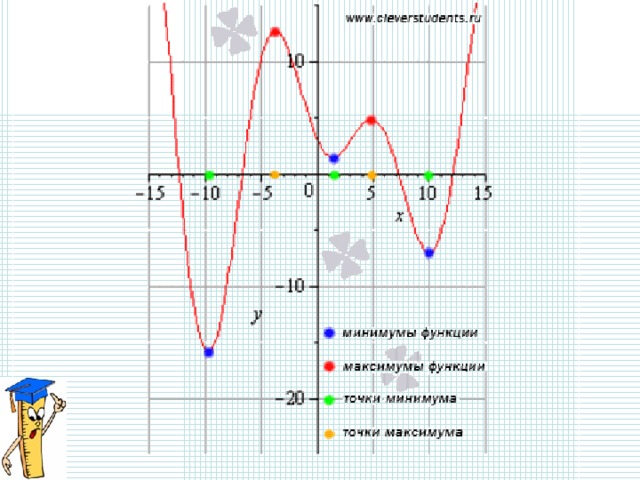
Точки минимума, точки максимума
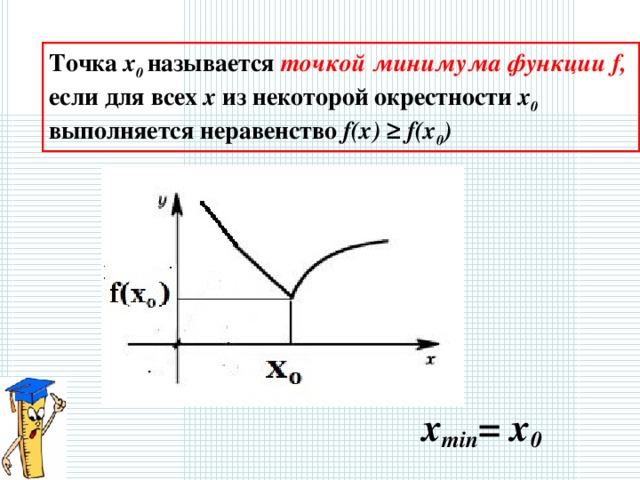
Точка х 0 называется точкой минимума функции f ,
если для всех х из некоторой окрестности х 0
выполняется неравенство f(x) ≥ f(x 0 )
x min = x 0
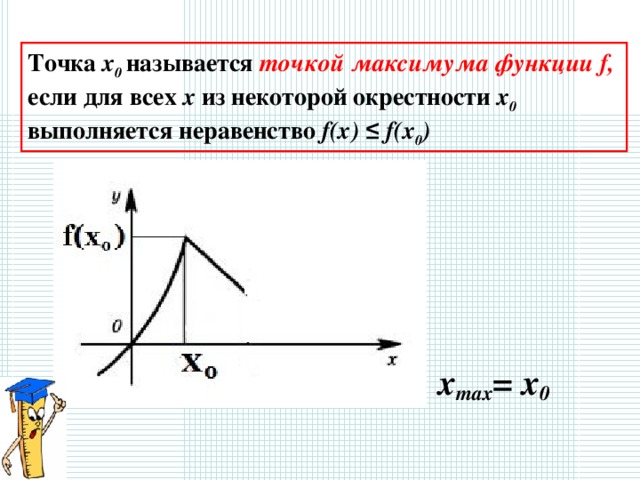
Точка х 0 называется точкой максимума функции f ,
если для всех х из некоторой окрестности х 0
выполняется неравенство f(x) ≤ f(x 0 )
x max = x 0

Спасибо за урок! Всем удачи!

 Получите свидетельство
Получите свидетельство Вход
Вход



![График функции, определенной на отрезке [-1;10]. Эта функция возрастает на отрезках [-1;3] и [4;5], и убывает на отрезках [3;4] и [5,10].](https://fsd.videouroki.net/html/2013/10/15/98666469/img1.jpg)

 x 1 , выполнено неравенство f(x 2 ) f(x 1 ). " width="640"
x 1 , выполнено неравенство f(x 2 ) f(x 1 ). " width="640"
 x 1 , выполнено неравенство f(x 2 ) 1 ). " width="640"
x 1 , выполнено неравенство f(x 2 ) 1 ). " width="640"
























 Возрастание и убывание функций. Экстремумы (0.61 MB)
Возрастание и убывание функций. Экстремумы (0.61 MB)
 2
2 5503
5503 1134
1134 Нравится
0
Нравится
0











