Функция и график функции

В ближайшее время все школы должны будут работать по ФГОС ООО. И учителю математики уже сегодня необходимо строить свою работу так, чтобы она соответствовала требованиям, которые предъявляет ФГОС к современному математическому образованию.

Одним из предметных результатов изучения предметной области «Математика и информатика» ФГОС определяет « овладение системой функциональных понятий, развитие умения использовать функционально-графические представления для решения различных математических задач, для описания и анализа реальных зависимостей».

Понятие функции в математике является основополагающим. К сожалению, даже успешные ученики не всегда могут дать определение функции. А уж «гуманитарии» и подавно не могут объяснить это важное понятие. Но функция это ещё и важное межпредметное понятие, используемое во всех без исключения предметах от алгебры и физики до экономики и литературы.

При изучении курса алгебры понятие графика функции можно использовать не только при изучении в рамках темы «Функция», но и во многих других разделах. А наличие в кабинете компьютера, мультимедиа и навыки работы с графопостроителями позволяют применять графики в исследовательской работе на уроке и вне его.

В своей работе я постоянно обращаюсь к понятию графика функции, чтобы к окончанию обучения (в 9 или 11 классе) ученик имел четкое представление о функции и способах применения функции и графика как при изучении предметной области «Математика и информатика», так и метапредметной (умение применять графический метод при самостоятельном решении проблем в других предметных областях).

Научное понятие функции и графика функции даётся в 7 классе на уроках алгебры. Но уже в 6 классе при изучении понятия «Координатная плоскость» и «График функции» необходимо сформировать у учеников начальные понятие по данной теме. Для этого в 6 классе я уже не первый год использую метод построения рисунков на координатной плоскости по готовым данным. А так же самостоятельное составление рисунков учениками. Такая форма работы очень нравится детям. Они с удовольствием сначала строят  рисунки по готовым координатам. Но  со временем у них появляется потребность придумывать и создавать свои рисунки. В 6 классе мы организуем проект-конкурс лучших работ. Ученики обмениваются своими работами и с удовольствием угадывают, что зашифровал координатами одноклассник. Результатом такой деятельности является прочное закрепление алгоритма построения точек на координатной плоскости, что немаловажно для дальнейшего изучения в курсе алгебры. Также в 6 классе я знакомлю учеников с компьютерной программой, строящей по координатам рисунки. Детям очень нравится такая работа, так как она похожа на компьютерную игру. Освоение работы с программой – первый шаг к освоению работы с графопостроителями на дальнейшей ступени обучения.

Также в 6 классе мы проводим практическую работу совместно с учителем географии по измерению температуры воздуха и построению на миллиметровой бумаге графиков зависимости температуры от времени суток. Благо весной, когда мы проводим эту работу, температура может значительно меняться  в течение суток, что характерно отражается на графиках. Такая работа соответствует требованиям ФГОС (метапредметным, включающим освоенные обучающимися межпредметные понятия и универсальные учебные действия (регулятивные, познавательные, коммуникативные), способность их использования в учебной, познавательной и социальной практике, самостоятельность планирования и осуществления учебной деятельности и организации учебного сотрудничества с педагогами и сверстниками, построение индивидуальной образовательной траектории). Таким образом, проводится пропедевтическая работа. К началу изучения  алгебры в 7 классе ученики владеют необходимой минимальной базой и начальными навыками исследовательской деятельности с применением средств ИКТ.

Рассмотрим примеры применения в курсе алгебры графиков функций при изучении различного учебного материала.

В 7 классе при изучении темы «Взаимное расположение графиков линейной функции» на уроке мы проводим исследование с целью выяснения от чего зависит взаимное расположение графиков. Составляем таблицу.

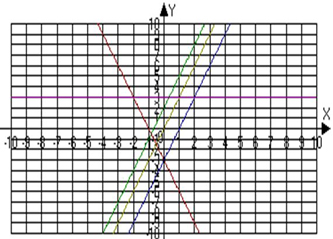
Затем предлагаю решить уравнения 3x+2=-3x-3 и т.п. и убедится в отсутствии или наличии корней. В итоге делам вывод и записываем свойство. В данной статье я привожу только примеры. На самом деле мы строим большое количество графиков до получения нужного результата.

Похожую работу мы проделываем при изучении темы «Решение систем линейных уравнений с двумя неизвестными». В рамках этой темы проводится урок-исследование «Графический способ решения систем уравнений с двумя неизвестными» где ученики на основании построений при помощи графопостроителя делают вывод о количестве решений системы.

 В 8 классе при изучении темы «График функции y=k/x» ученики исследуют расположение гиперболы в зависимости от коэффициента k.

Выполняем достаточное количество построений и делаем вывод.

Неоценимую помощь оказывает графопостроитель при изучении темы «Графическое решение уравнений». При изучении этого способа программа позволяет приводить большое количество примеров и научить верно, указывать ответ уравнения. А так же позволяет показать ученикам, что графически можно решить уравнения, решение которых им недоступно аналитическим способом.

В 9 классе при изучении темы «Квадратичная функция» с помощью графопостроителя экономится время на построения при отработке умения определять расположение параболы в зависимости от параметров. В последних вариантах ГИА мы видим задания вида: по графику квадратичной функции определить знаки параметров a, b и c.

При изучении темы «График квадратичной функции» проводим урок исследование. На котором учимся строить графики вида: y=ax²+n и y=a(x-m)².

Задание: 1) построить график y=x²; 2) y=x²-2; 3)y=x²+2.

На основании построений даем понятие параллельного переноса и делаем выводы о способах построения графиков при помощи параллельного переноса.

В 10 классе удобно применять графопостроитель при изучении темы «Графики тригонометрических функций». Здесь мы также проводим урок-исследование «Построение графиков вида y=sin(kx+n), cos(kx+n) и т.п.

При изучении темы «Применение производной» при помощи графиков можно наглядно показать взаимосвязь производной и функции, демонстрируя такие иллюстрации.

На рисунке дан график функции y=x² и график её производной y=2x. Ответьте на вопросы:

1) По графику функции: а) промежутки возрастания, убывания функции; б) точки экстремума.

2) По графику производной : а) промежутки знакопостоянства; б) нули.

Предлагаю большое количество таких иллюстраций. Анализируя и сопоставляя, ученики выдвигают гипотезу. Затем формулируем необходимые правила.

Также полезно применять иллюстрации при изучении темы «Касательная». Ученикам необходимо показать наглядно геометрический смысл производной.

В заданиях ЕГЭ в 11 классе необходимо по готовым рисункам определить значения производной. Выработке этого умения способствуют такие задания, которые можно предлагать на устном счете в 10 и 11 классах. Анализ работ ЕГЭ показывает, что ученики часто путают график функции с графиком производной. Поэтому необходимо сформировать умения по различным графикам считывать нужные данные.  Приведу примеры задач, формирующих такие умения.

1) По графику функции определить значения x, при которых а) производная равна нулю, б) положительна, в) отрицательна.

2) По графику производной определите: значения x, при которых функция: а) возрастает, б) убывает, в) точки экстремума, г) угловой коэффициент касательной положителен, отрицателен, равен нулю.

Затем приводим рисунок, на котором изображены график функции и график производной.

Таким образом, последовательная и логично построенная на протяжении всего курса работа над понятием функция и график функции позволяет формировать необходимые предметные и метапредметные умения при подготовке к работе по ФГОС ООО.