Цели:
1.Образовательные:
сформировать умения строить график линейной функции в частных случаях: график прямой пропорциональности, графики функции при одинаковом значении коэффициента, график постоянной функции.
2. Развивающие:
-создание условия для развития на уроке психологических качеств учащихся: интеллекта, мышления, памяти, внимания;
-обеспечить условия для развития познавательных процессов, для формирования общеучебных и специальных умений, совершенствованию мыслительных операций;
-создание условий для формирования ключевых компетенций: учебно-познавательной, коммуникативной, информационной, ценностно-смысловой, компетенции личностного самосовершенствования..
3. Воспитательные:
-обеспечить условия для формирования положительного отношения к знаниям, к процессу учения.
Задачи урока:
1.Образовательные:
-повторить известные приёмы построения графика линейной функции;
-научить строить график линейной функции в частных случаях;
-совершенствовать вычислительные навыки, навыки обработки информации.
2.Развивающие:
-совершенствовать умения самоконтроля и взаимоконтроля;
-развивать внимание, умения сравнивать, делать выводы и обобщения.
3.Воспитательные:
-создать условия для раскрытия коммуникативных способностей учащихся;
-побудить учащихся к активной мыслительной деятельности;
-прививать и укреплять умение давать полный и обоснованный ответ на поставленный вопрос.
Оборудование: Компьютерный класс. Программа для построения графиков «Аgrapher».
Ход урока:
I.Этап: Организационный момент.
II.Этап: Актуализация знаний:
Сообщение темы урока: «График линейной функции в частных случаях»
Вопросы:
- Как вы думаете: «Что мы будем делать сегодня на уроке?»
- Чему должны научиться к концу урока?
(ценностно-смысловая компетенция)
III.Этап: Изучение нового материала.
Учащиеся организуются в 3 группы (в классе 14 учащихся) по принципу взаимной симпатии. Каждая группа выбирает себе название.
Группа распределяет роли участников группы самостоятельно: кто осуществляет общий контроль за работой, кто готовит вывод о работе группы, кто проводит компьютерный контроль правильности решения, кто выступает о работе группы, внутри группы проводится самооценка работы каждого ученика. (формируются компетенции: учебно-познавательная, коммуникативная компетенции, компетентность личностного самосовершенствования)
Задание для групп:
1 группа:
1. В одной и той же системе координат постройте графики функций: у=2х, у=х, у=–2х, у=–0,5х.
2. Проверьте правильность построения графиков с помощью компьютера.
3. Сделайте вывод о том, что общего у всех этих графиков.
4. На стр.351 учебника найдите информацию о том, как называются все эти функции.
5. Выясните, в каких координатных четвертях расположены графики функций данного вида и от чего это зависит.
6. Выясните, какой угол образует график функции с положительным направлением оси Ох и от чего это зависит.
7. Подготовьте выступающих по итогам работы вашей группы.
8. Выставьте оценки в зависимости от личного участия каждого ученика в работе группы.
2 группа:
1. В одной и той же системе координат постройте графики функций: у=2х, у=2х+2, у=2х+4, у=2х–2.
2. Проверьте правильность построения графиков с помощью компьютера.
3. Сделайте вывод о том, что общего у всех этих графиков.
4. На стр.352 учебника найдите информацию о том, чем являются графики функций такого вида.
5. Выясните, как связан общий вид функции с точкой пересечения графика этой функции с осью Оу .
6. Выясните, какой угол образует график функции с положительным направлением оси Ох и от чего это зависит.
7. Подготовьте выступающих по итогам работы вашей группы.
8. Выставьте оценки в зависимости от личного участия каждого ученика в работе группы.
3 группа:
1. В одной и той же системе координат постройте графики функций: у=2х+1, у=–2х+1, у=х+1, у=0,5х+1.
2. Проверьте правильность построения графиков с помощью компьютера.
3. Сделайте вывод о том, что общего у всех этих графиков.
4. Найдите координаты общей точки пересечения графиков.
5. Выясните, как связан общий вид функции с точкой пересечения графика этой функции с осью Оу .
6. Выясните, какой угол образует график функции с положительным направлением оси Ох и от чего это зависит.
7. Подготовьте выступающих по итогам работы вашей группы.
8. Выставьте оценки в зависимости от личного участия каждого ученика в работе группы.
Учащиеся решают задачи карточки в группе: обсуждают решение, консультируют друг друга по возникающим вопросам, записывают решение в свою тетрадь. Готовят ученика для выступления, проверяют правильность решение по компьютеру, используя программу для построения графиков, например AGRAPHER. В случае затруднения в решении могут обратиться за помощью к учителю или любому другому ученику(даже не из своей группы). Заполняют лист оценок. (формируются компетенции: учебно-познавательная, коммуникативная, информационная, ценностно-смысловая, компетенция личностного самосовершенствования)
Роль учителя: минимальная помощь группе в случае необходимости, наблюдение за работой группы.
Решение: 1 группа
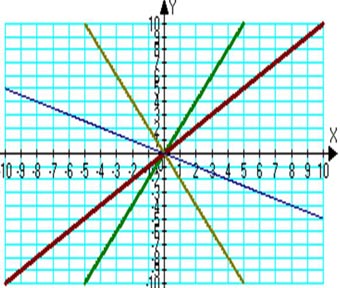
3.Все графики проходят через начало координат. 4.Функцию вида у=kx называют прямой пропорциональностью. 5.График функции лежит в 1 и 3 четвертях, если коэффициент k положительный, если k- отрицательное число, то во 2 и 4 четвертях. 6.Если k положительно, то угол между прямой и положительным направлением оси Ох острый, если k- отрицательное число, то этот угол – тупой.
2 группа:
3.У всех графиков одинаковый коэффициент k=2. 4.Графиками таких функций являются параллельные прямые.5.Точкой пересечения с Оу является точка с координатами (0;l) 6.Все эти прямые образуют острый угол с осью Ох(k-положительное число).
3 группа:
3.У всех графиков общее число l=1. 4. Общая точка пересечения имеет координаты (0;1). 5.Графики пересекают ось Оу в точке (0;l). 6. Если k положительно, то угол между прямой и положительным направлением оси Ох острый, если k- отрицательное число, то этот угол – тупой.
IV.Этап: Защита работы
Ученики из каждой группы, подготовленные группой по своей карточке, делают сообщение о работе группы. Обязательно акцентируют внимание на выводах.
Другая группа внимательно выслушивает ответы, задает вопросы по мере необходимости. Отвечающий ученик или участник группы дает необходимые пояснения. Группа выставляет оценку отвечающему ученику в свой лист оценок (дописывают его фамилию в конец списка). Учитель подводит краткий итог работы групп по карточкам.
По завершении обсуждения ответов групп учителем задается вопрос: Как будет выглядеть график функции в случае, если коэффициент k=0, т.е. формула имеет вид у=5, у=3, у=–2 и.т.д.? Какая группа найдет ответ быстрее? (При необходимости: Подсказка- можно воспользоваться текстом учебника на стр.353: функцию у=l называют постоянной функцией. Графики таких постоянных функций параллельны оси Ох и проходят через точку l)
V.Этап: Творческая работа в группе.
Каждая группа готовит задание для других групп по теме своей карточки. Обмениваются заданиями. Выполняют их. Проводят взаимоконтроль. (при затруднении в выполнении задания разрешается воспользоваться подсказкой ученика из группы, предложившей задание или провести компьютерный контроль)
VI.Этап: Закрепление.
Самостоятельная работа (в парах или группах по 3-4 учащихся): № 1366, 1367, 1369. Дополнительное задание: № 1365, 1364, 1363.
VII.Этап: Домашнее задание: § 44-читать, выучить определения. № 1362, 1367. Творческое задание: Придумать задачи по теме «График линейной функции».
VIII/Этап: Рефлексия.
Вопросы:
- Что нового узнали на уроке?
- Понравилось ли вам работать в группе?
- Что хорошего вы заметили на уроке?
- Как сделать работу на уроке более интересной?
Подведение итогов. Выставление оценок.
Лист оценок группы 6А класса:______________________________________________________
График линейной функции в частных случаях. Дата:__________________________ 2013 года.
|
Фамилия,И. ученика |
самооценка |
Оценка группы |
Другие оценки |
|||
|
Защита ответа группы |
взаимоконтроль |
Дополнительные задания |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При выставлении оценок руководствоваться следующими принципами:
- Самооценка- ученик сам ставит себе оценку за решение заданий карточки; «5»- если решил правильно и самостоятельно, «4» - если решил правильно, но обращался за помощью к другим ученикам или учителю за незначительными разъяснениями, «3» в другом случае, кроме «2» когда задания не решены.
- Оценка группы: выставляется ученику группой за его вклад в работу группы: «5»-активно работал, давал консультации другим, «4»- активно работал, по некоторым вопросам возникали трудности, «3»- в других случаях, «2»- в исключительных случаях.
- Другие оценки- ставятся ученику за выполнение других заданий: за ответ по итогам работы группы, взаимоконтроль, дополнительные задания. «5»- выполнено верно, без ошибок, «4»- выполнено верно, допущены 1-2 ошибки, «3»-выполнено, но допущено более 2 ошибок, «2»-не выполнено.
Итоговая оценка за урок выставляется с учетом всех оценок при этом преимуществом пользуются оценки полученные в плане самооценки и взаимоконтроля.
На следующем уроке дается самостоятельная работа в двух вариантах по задачам карточки, по которой группа не готовила ответ. Если большинство учеников правильно решает задания своего варианта, то тому ученику, кто защищал эту тему на предыдущем уроке, выставляется дополнительная оценка, полученная им как оценка за ответ группы. (если ученик согласен с этой оценкой).
В итоге все ученики активно работают на уроке, решают задания, объясняют решение партнерам и вновь решают. При этом формируются ключевые компетенции: учебно-познавательная, коммуникативная, информационная, ценностно-смысловая, компетенция личностного самосовершенствования и другие.

 Получите свидетельство
Получите свидетельство Вход
Вход


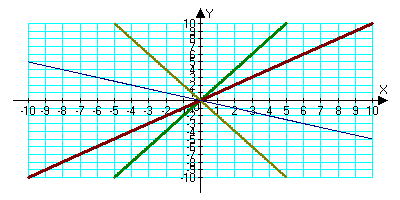
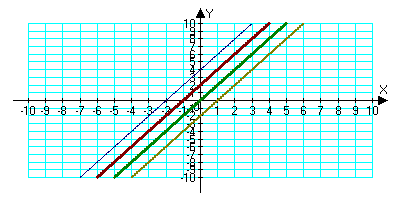
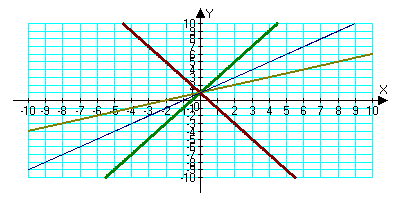









 График линейной функции в частных случаях (45.43 КB)
График линейной функции в частных случаях (45.43 КB)
 1
1 2028
2028 109
109 Нравится
0
Нравится
0



