Игра по математике "Звездный час"

Цели: 

• повторить графики и свойства всех изученных в школьном курсе функций;
• повторить построение графика функции с помощью производной;
• развитие внимания, умения размышлять, умения правильно делать выбор.

Современная математика знает множество функций, и у каждой функции свой неповторимый облик, как неповторим облик каждого из семи миллиардов людей, живущих на Земле.

     Однако при всей непохожести одного человека на другого у каждого есть руки и голова, уши и глаза.

Функции – это математические портреты устойчивых закономерностей, познаваемых человеком. Чтобы проиллюстрировать характерные свойства функций обратимся к пословицам. Ведь пословицы это тоже отражение устойчивых закономерностей, выверенные многовековым опытом народа.

     «Чем дальше в лес, тем больше дров» - гласит пословица. Изобразим графиком, как нарастает количество дров по мере продвижения в глубь леса – от опушки, где всё давным-давно собрано, до чащоб, куда ещё не ступала нога заготовителя.

      Горизонтальная ось графика – это лесная дорога. По вертикали будем откладывать (допустим, в кубометрах) количество топлива на данном километре дороги.

     График представит количество дров как функцию пути.

     Согласно пословице эта функция неизменно возрастает. Какие две точки на оси абсцисс ни взять, для более дальней (чем больше в лес…) значение функции будет больше (…тем больше дров). Такое свойство функции называется монотонным возрастанием.

«Выше меры конь не скачет». Если  изобразить траекторию скачущего коня, то высота скачков в полном соответствии с пословицей будет ограничена сверху некоторой «мерой». Вот знакомый график синуса. И здесь есть своя мера, выше которой не вздымаются волны синусоиды. Такой мерой, такой непереступаемой верхней гранью может послужить и десятка, и семерка, и тройка, и единица.

Единица среди всех перечисленных величин на особом положении: это точная верхняя грань для значений синуса.

В каком же смысле она точна? В том, очевидно, что понизить её уже нельзя. Для любого уровня, что ниже точной  верхней грани, найдутся значения функции, его превосходящие. В этом одно из двух отличительных свойств точной верхней грани. А другое и совсем очевидно: её не превосходит ни одно значение функции.

Обратите внимание на выражение: «не превосходит». Это значит «меньше или равно». Синус и в самом деле кое-где равен единице – в точках, соответствующих макушкам волн. Во всех остальных он меньше единицы.

Есть у значений синуса и точная нижняя грань – минус единица.

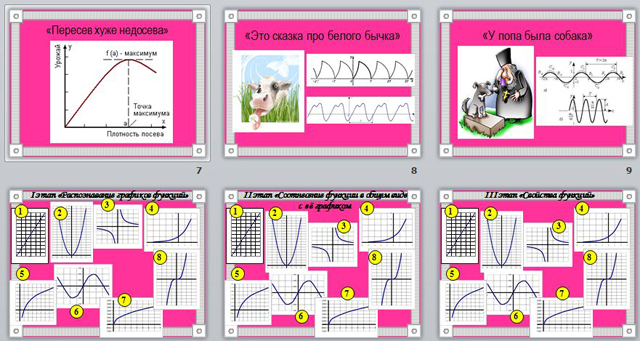
«Пересев хуже недосева», - издавна говорили земледельцы. Вековой опыт свидетельствовал: урожай лишь до некоторой поры растет вместе с плотностью посева, дальше он снижается, потому что при чрезмерной густоте ростки начинают глушить друг друга.

Эта закономерность станет особенно наглядной, если изобразить её графиком, где урожай представлен как функция плотности посева. Урожай максимален, когда поле засеяно в меру. Максимум – это наибольшее значение функции по сравнению с её значениями во всех соседних точках. Это как бы вершина горы, с которой все дороги ведут только вниз, куда ни шагни.

В примере с урожаем дело обстоит точно так же, как в той застольной ситуации, которую описывает пословица «Недосол на столе – пересол на спине». Качество пищи зависит, является функцией от количества соли в ней. Мало соли – невкусно, много – тоже в рот не возьмешь. А где-то в промежутке, в золотой середине, когда соли в самый раз, кушанье становится особенно лакомым. В этой точке кулинарная функция достигает максимума. Малейшей щепотью соли больше или меньше – и дегустатор с утонченным вкусом скажет, сто качество пищи снизилось.

Есть у максимума антипод – минимум. Минимум – это как бы дно впадины, из которой, куда ни шагни, все дороги ведут только вверх.

«Это сказка про белого бычка». Так говорят, когда какое-то дело безнадежно затягивается, когда раз за разом попытки уладить его приводят к пустому или бессмысленному результату.

Поговорку знают все, но не каждый знает, как рассказывается сказка. Важная деталь рассказа – реакция слушателя. Сказка представляет  собой диалог:

- Рассказать тебе сказку про белого бычка?

- Расскажи.

Ты расскажи, я расскажи. Рассказать тебе сказку про белого бычка?

- Так давай же!

Ты так давай же, я так давай же. Рассказать тебе сказку про белого бычка?

- Ну хватит!

- Ты ну хватит, я ну хватит. Рассказать тебе сказку про белого бычка? И так далее.

            Ссылку на сказку про белого бычка часто заменяют на цитирование первых слов песни «У попа была собака». Ради полноты приведем её. «У попа была собака. Он её любил. Она съела кусок мяса. Он её убил. И в землю закопал. И надпись написал: «У попа была собака. Он её любил…»». И так далее.

Белый бычок и поповская собака нужны нам для разговора о периодических функциях, для уяснения математического понятия периода.

Так на пословицах и поговорках мы попытались объяснить некоторые свойства функций.

А сейчас начинаем игру звездный час на тему «Функция». В процессе игры вы покажете, как вы знаете свойства функций, умение читать графики функций, умение строить графики функций.

Игра состоит из 5 этапов. На первых трех этапах вы будете работать с графиками функций, отвечать на вопросы, поднимая соответствующий номер. Тот, кто ответит на вопрос правильно, получает звезду. После каждого этапа будет подводиться итог, после чего участник, набравший меньше всего звезд, покидает игру. На 5 этапе должны остаться только два участника, в ходе которого и определится победитель. Итак, начинаем. На слайде восемь графиков функций

I этап «Распознавание графиков функций»

Вопросы:

1. Указать график логарифмической функции (5)
2. Указать график квадратичной функции (2)
3. Указать график тригонометрической функции (6)
4. Указать график линейной функции (1)
5. Указать график показательной функции (4)
6. Указать график кубической параболы (8)
7. Указать график степенной функции (7)
8. Указать график обратной пропорциональной зависимости (3)

Подводим итог первого этапа. Участник с меньшим количеством звезд покидает игру.

II этап «Соотношение функций в общем виде с её графиком» (смотри архив)

III этап «Свойства функций» (смотри архив)

Подводим итог третьего этапа. Участник с меньшим количеством звезд покидает игру.

IV Этап «Построение графика функции»

«С помощью производной построить график функции y = x³ +6x² + 9x»

Подводим итог четвертого этапа. Участник с меньшим количеством звезд покидает игру.

V Этап «Суперигра»

За одну минуту составить как можно больше слов из букв входящих в слово «производная». Болельщики тоже составляют слова. После того как время закончится, игрок может выбрать себе помощника из болельщиков, и воспользоваться его словами. Если слова закончились, то можно вместо слов ставить звезду. Победит тот, кто скажет последнее слово.

Подведение итогов. Церемония награждения.

Литература:

Попов Ю.П., Пухначев Ю.В. «Математика в образах» - М.: Знание, 1089. – 208 с. – (нар. ун-т. Естественнонаучный фак.)